|
|
| Доклад: Аппроксимация функций |
Доклад: Аппроксимация функций
Аппроксимация функций.
Из курса математики известны 3 способа задания функциональных зависимостей:
1) аналитический
2) графический
3) табличный
Табличный способ обычно возникает в результате эксперемента.
Недостаток табличного задания функции заключается в том, что найдутся значения
переменных которые неопределены таблицей. Для отыскания таких значений
определяют приближающуюся к заданной функцию, называемой аппроксмирующей,
а действие замены аппроксимацией.
Аппроксимация заключается в том, что используя имеющуюся информацию по
f(x) можно рассмотреть другую функцию φ(ч) близкую в некотором смысле к
f(x), позволяющую выполнить над ней соответствующие операции и получить оценку
погрешность такой замены.
φ(х)- аппроксимирующая функция.
Интерполяция (частный случай аппроксимации)
Если для табличной функции y=f(x), имеющей значение x0 f(x0
) требуется построить аппроксимирующюю функцию j(x) совпадающую в узлах с x
i c заданной, то такой способ называется интерполяцией
При интерполяции, заданная функция f(x) очень часто аппроксимируется с
помощью многочлена, имеющего общий вид
j(x)=pn(x)=anxn+an-1xn-1+.+a0
В данном многочлене необходимо найти коэффициенты an ,an-1
, .a0 , так как задачей является интерполирование, то определение
коэффициентов необходимо выполнить из условия равенства:
Pn(xi)=yi i=0,1,.n
Для определения коэффициентов применяют интерполяционные многочлены специального
вида, к ним относится и полином Лагранжа Ln(x).
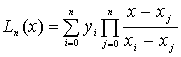 i¹j
В точках отличных от узлов интерполяции полином Лагранжа в общем случае не
совпадает с заданной функцией . i¹j
В точках отличных от узлов интерполяции полином Лагранжа в общем случае не
совпадает с заданной функцией .
Задание
С помощью интерполяционного полинома Лагранжа вычислить значение функции y в
точке xc, узлы интерполяции расположены равномерно с шагом Dх=4,1
начиная с точки х0=1,3 даны значения функции
y={-6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27}.
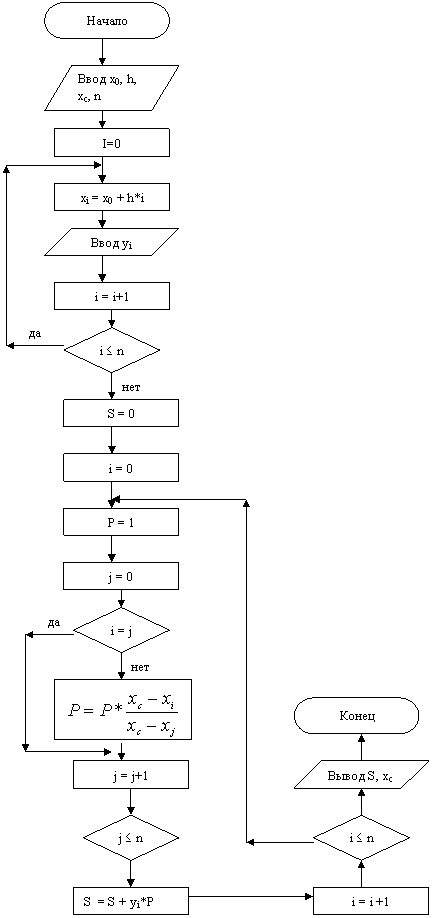
ГСА для данного метода
 CLS
DIM Y(9)
DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27
X0 = 1.3: H = 4.1: N = 10: XC = 10
FOR I = 0 TO N - 1
1 X(I) = X0 + H * I
READ Y(I)
PRINT Y(I); X(I)
NEXT I
S1 = 0: S2 = 0: S3 = 0: S4 = 0
FOR I = 0 TO N - 1
2 S1 = S1 + X(I) ^ 2
S2 = S2 + X(I)
S3 = S3 + X(I) * Y(I)
S4 = S4 + Y(I)
NEXT I
D = S1 * N - S2 ^ 2
D1 = S3 * N - S4 * S2
D0 = S1 * S4 - S3 * S2
A1 = D1 / D: A0 = D0 / D
YC = A1 * XC + A0
PRINT "A0="; A0, "A1="; A1, "YC="; YC
FOR X = 0 TO 50 STEP 10
Y = A1 * X + A0
PRINT X, Y
NEXT X
END
XC= 10
Х Y
1.3 -6.56
5.4 -3.77
9.5 -1.84
13.6 .1
17.7 2.29
21.8 4.31
25.9 5.86
30 8.82
34.1 11.33
38.2 11.27
S=-1.594203
АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
В инженерной деятельности часто возникает необходимость описать в виде
функциональной зависимости связь между величинами, заданными таблично или в
виде набора точек с координатами (xi,yi),
i=0,1,2,...n, где n - общее количество точек. Как правило, эти
табличные данные получены экспериментально и имеют погрешности. При
аппроксимации желательно получить относительно простую функциональную
зависимость (например, полином), которая позволила бы "сгладить"
экспериментальные погрешности, получить промежуточные и экстраполяционные
значения функций, изначально не содержащиеся в исходной табличной информации.
Графическая интерпретация аппроксимации.
Эта функциональная (аналитическая) зависимость должна с достаточной точностью
соответствовать исходной табличной зависимости. Критерием точности или
достаточно "хорошего" приближения могут служить несколько условий.
Обозначим через fi значение, вычисленное из функциональной
зависимости для x=xi и сопоставляемое с yi
.
Одно из условий согласования можно записать как
S =
CLS
DIM Y(9)
DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27
X0 = 1.3: H = 4.1: N = 10: XC = 10
FOR I = 0 TO N - 1
1 X(I) = X0 + H * I
READ Y(I)
PRINT Y(I); X(I)
NEXT I
S1 = 0: S2 = 0: S3 = 0: S4 = 0
FOR I = 0 TO N - 1
2 S1 = S1 + X(I) ^ 2
S2 = S2 + X(I)
S3 = S3 + X(I) * Y(I)
S4 = S4 + Y(I)
NEXT I
D = S1 * N - S2 ^ 2
D1 = S3 * N - S4 * S2
D0 = S1 * S4 - S3 * S2
A1 = D1 / D: A0 = D0 / D
YC = A1 * XC + A0
PRINT "A0="; A0, "A1="; A1, "YC="; YC
FOR X = 0 TO 50 STEP 10
Y = A1 * X + A0
PRINT X, Y
NEXT X
END
XC= 10
Х Y
1.3 -6.56
5.4 -3.77
9.5 -1.84
13.6 .1
17.7 2.29
21.8 4.31
25.9 5.86
30 8.82
34.1 11.33
38.2 11.27
S=-1.594203
АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
В инженерной деятельности часто возникает необходимость описать в виде
функциональной зависимости связь между величинами, заданными таблично или в
виде набора точек с координатами (xi,yi),
i=0,1,2,...n, где n - общее количество точек. Как правило, эти
табличные данные получены экспериментально и имеют погрешности. При
аппроксимации желательно получить относительно простую функциональную
зависимость (например, полином), которая позволила бы "сгладить"
экспериментальные погрешности, получить промежуточные и экстраполяционные
значения функций, изначально не содержащиеся в исходной табличной информации.
Графическая интерпретация аппроксимации.
Эта функциональная (аналитическая) зависимость должна с достаточной точностью
соответствовать исходной табличной зависимости. Критерием точности или
достаточно "хорошего" приближения могут служить несколько условий.
Обозначим через fi значение, вычисленное из функциональной
зависимости для x=xi и сопоставляемое с yi
.
Одно из условий согласования можно записать как
S =
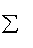 (fi-yi) ® min ,
т.е. сумма отклонений табличных и функциональных значений для одинаковых x=x
i должна быть минимальной (метод средних). Отклонения могут иметь
разные знаки, поэтому достаточная точность в ряде случаев не достигается.
Использование критерия S = (fi-yi) ® min ,
т.е. сумма отклонений табличных и функциональных значений для одинаковых x=x
i должна быть минимальной (метод средних). Отклонения могут иметь
разные знаки, поэтому достаточная точность в ряде случаев не достигается.
Использование критерия S =
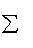 |fi-y
i| ® min , также не приемлемо, т.к. абсолютное значение не имеет
производной в точке минимума.
Учитывая вышеизложенное, используют критерий наименьших квадратов
, т.е. определяют такую функциональную зависимость, при которой
S =
(fi-yi)2 , (1)
обращается в минимум.
В качестве функциональной зависимости рассмотрим многочлен
f(x)=C0 + C1X + C2X2+...+CMXM. (2)
Формула (1) примет вид S = |fi-y
i| ® min , также не приемлемо, т.к. абсолютное значение не имеет
производной в точке минимума.
Учитывая вышеизложенное, используют критерий наименьших квадратов
, т.е. определяют такую функциональную зависимость, при которой
S =
(fi-yi)2 , (1)
обращается в минимум.
В качестве функциональной зависимости рассмотрим многочлен
f(x)=C0 + C1X + C2X2+...+CMXM. (2)
Формула (1) примет вид S =
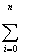 ( C0 + C1Xi + C2Xi2+...+CMXiM - Yi ) 2
Условия минимума S можно записать, приравнивая нулю частные производные S по
независимым переменным С0,С1,...СМ :
SC0 = 2
( C0 + C1 ( C0 + C1Xi + C2Xi2+...+CMXiM - Yi ) 2
Условия минимума S можно записать, приравнивая нулю частные производные S по
независимым переменным С0,С1,...СМ :
SC0 = 2
( C0 + C1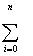 Xi + C2 Xi + C2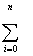 Xi2+...+CM Xi2+...+CM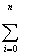 XiM - Yi ) = 0 ,
SC1 = 2
( C0 + C1 XiM - Yi ) = 0 ,
SC1 = 2
( C0 + C1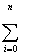 Xi + C2 Xi + C2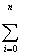 Xi2+...+CM Xi2+...+CM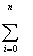 XiM - yi ) Xi = 0 ,
.............................................................................
.................... (3)
SCM = 2
( C0 + C1 XiM - yi ) Xi = 0 ,
.............................................................................
.................... (3)
SCM = 2
( C0 + C1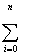 Xi + C2 Xi + C2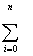 Xi2+...+CM Xi2+...+CM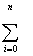 XiM - Yi ) XiM = 0 ,
Тогда из (3) можно получить систему нормальных уравнений
C0 XiM - Yi ) XiM = 0 ,
Тогда из (3) можно получить систему нормальных уравнений
C0 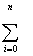 (N+1) + C1 (N+1) + C1
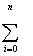 Xi + C2 Xi + C2
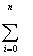 Xi2 +...+ CM Xi2 +...+ CM
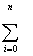 XiM = XiM =
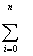 Yi ,
C0 Yi ,
C0
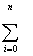 Xi + C1 Xi + C1
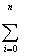 Xi2 + C2 Xi2 + C2
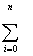 Xi3 +...+ CM Xi3 +...+ CM
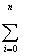 XiM+1 = XiM+1 =
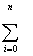 Yi Xi ,
.......................................................................................................
(4)
C0 Yi Xi ,
.......................................................................................................
(4)
C0
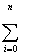 XiM + C1 XiM + C1
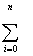 XiM+1 + C2 XiM+1 + C2
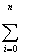 XiM+2 +...+ CM XiM+2 +...+ CM
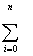 Xi2M = Xi2M =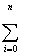 Yi XiM .
Для определения коэффициентов Сi и, следовательно, искомой
зависимости (2) необходимо вычислить суммы и решить систему уравнений (4).
Матрица системы (4) называется матрицей Грама и является симметричной и
положительно определенной. Эти полезные свойства используются при ее решении.
Yi XiM .
Для определения коэффициентов Сi и, следовательно, искомой
зависимости (2) необходимо вычислить суммы и решить систему уравнений (4).
Матрица системы (4) называется матрицей Грама и является симметричной и
положительно определенной. Эти полезные свойства используются при ее решении.
| (N+1) | 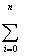 Xi Xi
| 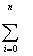 Xi2 Xi2
| ... | 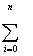 XiM XiM
| 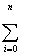 Yi Yi
| | | Xi | 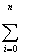 Xi2 Xi2
| 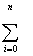 Xi3 Xi3
| ... | 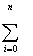 XiM+1 XiM+1
| 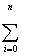
Yi Xi | | | ... | ... | ... | ... | ... | ... | | | XiM | 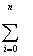 XiM+1 XiM+1
| 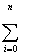 XiM+2 XiM+2
| ... | 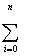 Xi2M Xi2M
| 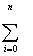 Yi XiM Yi XiM
| |
Нетрудно видеть, что для формирования расширенной матрицы (4а) достаточно
вычислить только элементы первой строки и двух последних столбцов, остальные
элементы не являются "оригинальными" и заполняются с помощью циклического
присвоения.
Задание
Найти коэффициенты прямой и определить значение функции y{-6.56,-3.77,
-1.84,0.1,2.29,4.31,5.56,8.82,11.33,11.27}, x0=1.3 h=4.1, и определить
интеграл заданной функции.
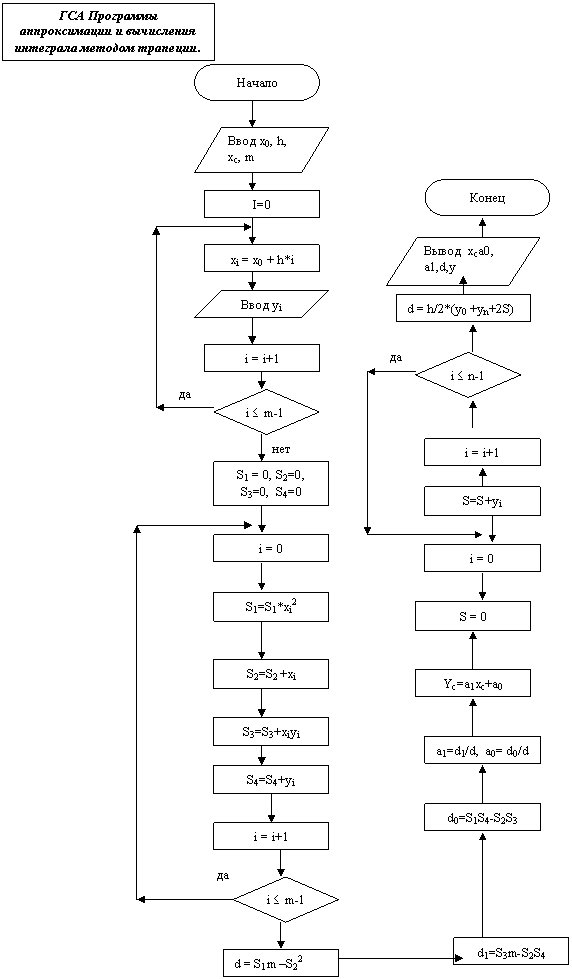
Программа
¦CLS
¦XC = 10: X0 = 1.3: H = 4.1: N = 10
¦DIM Y(9): DIM X(9)
¦DATA -6.56,-3.77,-1.84,0.1,2.29,4.31,5.86,8.82,11.33,11.27
¦FOR I = 0 TO N - 1
¦X = X0 + H * I:
¦X(I) = X
¦READ Y(I)
¦PRINT X(I), Y(I)
¦NEXT I
¦S1 = 0: S2 = 0: S3 = 0: S4 = 0
¦I = 0
¦10 S1 = S1 + X(I) ^ 2:
¦S2 = S2 + X(I):
¦S3 = S3 + X(I) * Y(I):
¦S4 = S4 + Y(I)
¦I = I + 1
¦IF I <= N - 1 THEN 10
¦D = S1 * N - S2 ^ 2:
¦D1 = S3 * N - S2 * S4:
¦D0 = S1 * S4 - S2 * S3
¦A1 = D1 / D:
¦A0 = D0 / D
¦Y = A1 * XC + A0
¦PRINT TAB(2); "КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A0="; A0,
¦PRINT TAB(2); "КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A1="; A1,
¦PRINT TAB(2); "ЗНАЧЕНИЕ ФУНКЦИИ В ТОЧКЕ XC Y="; Y
¦FOR X = 10 TO 50 STEP 10
¦Y = A1 * X + AO
¦PRINT X, Y
¦NEXT X
¦FOR I = 1 TO N - 1
¦S = S + Y(I): NEXT I
¦D = H / 2 * (Y(0) + Y(N - 1) + 2 * S)
¦PRINT "ЗНАЧЕНИЕ ИНТЕГРАЛА ПО МЕТОДУ ТРАПЕЦИИ D="; D
Ответы
Х Y
1.3 -6.56
5.4 -3.77
9.5 -1.84
13.6 .1
17.7 2.29
21.8 4.31
25.9 5.86
30 8.82
34.1 11.33
38.2 11.27
КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A0=-6.709182
КОЭФФИЦИЕНТ ПРЯМОЙ В ТОЧКЕ A1= .5007687
ЗНАЧЕНИЕ ФУНКЦИИ В ТОЧКЕ XC Y=-1.701495
10 5.007687
20 10.01537
ЗНАЧЕНИЕ ИНТЕГРАЛА ПО МЕТОДУ ТРАПЕЦИИ D= 166.9725
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



