|
|
| Доклад: Метод Симпсона |
Доклад: Метод Симпсона
Кафедра «Высшей математики»
Реферат:
 Выполнил: Матвеев Ф.И.
Проверила: Бурлова Л.В.
Улан-Удэ.2002
Содержание.
1.Численные методы интегрирования
2.Вывод формулы Симпсона
3.Геометрическая иллюстрация
4.Выбор шага интегрирования
5.Примеры
1. Численные методы интегрирования
Задача численного интегрирования заключается в вычислении интеграла
Выполнил: Матвеев Ф.И.
Проверила: Бурлова Л.В.
Улан-Удэ.2002
Содержание.
1.Численные методы интегрирования
2.Вывод формулы Симпсона
3.Геометрическая иллюстрация
4.Выбор шага интегрирования
5.Примеры
1. Численные методы интегрирования
Задача численного интегрирования заключается в вычислении интеграла
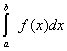 посредством ряда значений подынтегральной функции посредством ряда значений подынтегральной функции 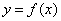 .
Задачи численного интегрирования приходится решать для функций, заданных
таблично, функцией, интегралы от которых не берутся в элементарных функциях,
и т.д. Рассмотрим только функции одной переменной.
Вместо функции, которую требуется проинтегрировать, проинтегрируем
интерполяционный многочлен. Методы, основанные на замене подынтегральной
функции интерполяционным многочленом, позволяют по параметрам многочлена
оценить точность результата или же по заданной точности подобрать эти
параметры.
Численные методы условно можно сгруппировать по способу аппроксимации
подынтегральной функции.
Методы Ньютона-Котеса основаны на аппроксимации функции .
Задачи численного интегрирования приходится решать для функций, заданных
таблично, функцией, интегралы от которых не берутся в элементарных функциях,
и т.д. Рассмотрим только функции одной переменной.
Вместо функции, которую требуется проинтегрировать, проинтегрируем
интерполяционный многочлен. Методы, основанные на замене подынтегральной
функции интерполяционным многочленом, позволяют по параметрам многочлена
оценить точность результата или же по заданной точности подобрать эти
параметры.
Численные методы условно можно сгруппировать по способу аппроксимации
подынтегральной функции.
Методы Ньютона-Котеса основаны на аппроксимации функции 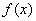 полиномом степени
полиномом степени 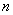 .
Алгоритм этого класса отличается только степенью полинома. Как правило, узлы
аппроксимирующего полинома – равноотносящие.
Методы сплайн-интегрирования базируются на аппроксимации функции .
Алгоритм этого класса отличается только степенью полинома. Как правило, узлы
аппроксимирующего полинома – равноотносящие.
Методы сплайн-интегрирования базируются на аппроксимации функции 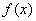 сплайном-кусочным полиномом.
В методах наивысшей алгебраической точности (метод Гаусса) используются
специально выбранные неравноотносящие узлы, обеспечивающие минимальную
погрешность интегрирования при заданном (выбранном) количестве узлов.
Методы Монте-Карло используются чаще всего при вычислении кратных интегралов,
узлы выбираются случайным образом, ответ носит вероятностный характер.
сплайном-кусочным полиномом.
В методах наивысшей алгебраической точности (метод Гаусса) используются
специально выбранные неравноотносящие узлы, обеспечивающие минимальную
погрешность интегрирования при заданном (выбранном) количестве узлов.
Методы Монте-Карло используются чаще всего при вычислении кратных интегралов,
узлы выбираются случайным образом, ответ носит вероятностный характер.
 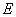
 суммарная погрешность
суммарная погрешность
 погрешность усечения
погрешность округления
погрешность усечения
погрешность округления
  Независимо от выбранного метода в процессе численного интегрирования
необходимо вычислить приближенное значение интеграла и оценить погрешность.
Погрешность уменьшается при увеличении n-количества
разбиений отрезка
Независимо от выбранного метода в процессе численного интегрирования
необходимо вычислить приближенное значение интеграла и оценить погрешность.
Погрешность уменьшается при увеличении n-количества
разбиений отрезка 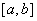 . Однако при этом возрастает погрешность округления
за счет суммирования значений интегралов, вычисленных на частичных отрезках.
Погрешность усечения зависит от свойств подынтегральной функции и длины . Однако при этом возрастает погрешность округления
за счет суммирования значений интегралов, вычисленных на частичных отрезках.
Погрешность усечения зависит от свойств подынтегральной функции и длины 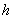 частичного отрезка.
2. Вывод формулы Симпсона
Если для каждой пары отрезков
частичного отрезка.
2. Вывод формулы Симпсона
Если для каждой пары отрезков 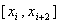 построить многочлен второй степени, затем проинтегрировать его и воспользоваться
свойством аддитивности интеграла, то получим формулу Симпсона.
построить многочлен второй степени, затем проинтегрировать его и воспользоваться
свойством аддитивности интеграла, то получим формулу Симпсона.
 Рассмотрим
подынтегральную функцию Рассмотрим
подынтегральную функцию 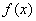 на отрезке
на отрезке 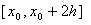 . Заменим
эту подынтегральную функцию интерполяционным многочленом Лагранжа второй
степени, совпадающим с . Заменим
эту подынтегральную функцию интерполяционным многочленом Лагранжа второй
степени, совпадающим с 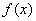 в точках
в точках 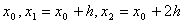 : :
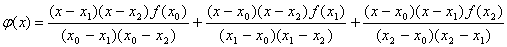 Проинтегрируем
Проинтегрируем 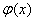 :
Формула: :
Формула:
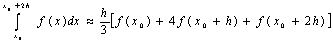 и называется формулой Симпсона.
Полученное для интеграла
и называется формулой Симпсона.
Полученное для интеграла 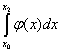 значение совпадает с площадью криволинейной трапеции, ограниченной осью
значение совпадает с площадью криволинейной трапеции, ограниченной осью 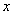 , прямыми
, прямыми 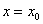 , , 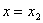 и параболой, проходящей через точки
и параболой, проходящей через точки 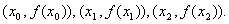 Оценим теперь погрешность интегрирования по формуле Симпсона. Будем считать,
что у
Оценим теперь погрешность интегрирования по формуле Симпсона. Будем считать,
что у 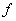 на отрезке на отрезке 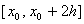 существуют непрерывные производные
существуют непрерывные производные 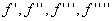 . Составим разность
. Составим разность
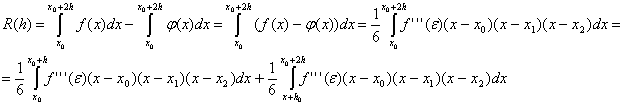 К каждому из этих двух интегралов уже можно применить теорему о среднем,
поскольку
К каждому из этих двух интегралов уже можно применить теорему о среднем,
поскольку 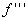 непрерывна на
непрерывна на 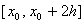 и
функция и
функция 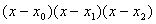 неотрицательна на первом интервале интегрирования и неположительна на втором (
то есть не меняет знака на каждом из этих интервалов). Поэтому:
неотрицательна на первом интервале интегрирования и неположительна на втором (
то есть не меняет знака на каждом из этих интервалов). Поэтому:
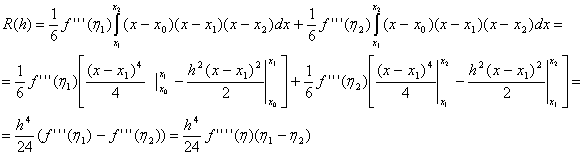 (мы воспользовались теоремой о среднем, поскольку
(мы воспользовались теоремой о среднем, поскольку 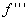 - непрерывная функция; - непрерывная функция; 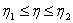 ).
Дифференцируя ).
Дифференцируя 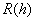 дважды и применяя затем теорему о среднем, получим для
дважды и применяя затем теорему о среднем, получим для 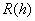 другое выражение:
другое выражение:
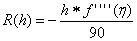 , где , где 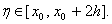 Из обеих оценок для
Из обеих оценок для 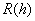 следует, что формула Симпсона является точной для многочленов степени не выше
третьей. Запишем формулу Симпсона, напрмер, в виде:
следует, что формула Симпсона является точной для многочленов степени не выше
третьей. Запишем формулу Симпсона, напрмер, в виде:
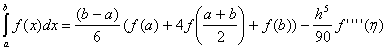 , ,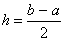 .
Если отрезок .
Если отрезок 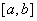 интегрирования слишком велик, то его разбивают на
интегрирования слишком велик, то его разбивают на 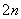 равных частей (полагая
равных частей (полагая 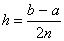 ), после чего к каждой паре соседних отрезков
), после чего к каждой паре соседних отрезков 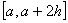 ,
, 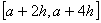 ,..., ,...,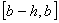 применяют формулу Симпсона, именно:
Запишем формулу Симпсона в общем виде:
применяют формулу Симпсона, именно:
Запишем формулу Симпсона в общем виде:
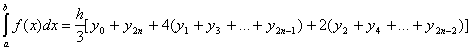 (1)
(1)
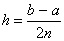 (2)
Погрешность формулы Симпсона - метода четвертого порядка: (2)
Погрешность формулы Симпсона - метода четвертого порядка:
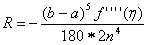 , , 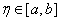 (3)
Так как метод Симпсона позволяет получить высокую точность, если (3)
Так как метод Симпсона позволяет получить высокую точность, если 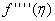 не слишком велика. В противном случае метод второго порядка может дать
большую точность.
Например, для функции
не слишком велика. В противном случае метод второго порядка может дать
большую точность.
Например, для функции 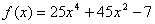 форма трапеции при
форма трапеции при 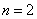 для
для 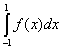 дает точный
результат дает точный
результат 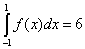 , тогда
как по формуле Симпсона получаем , тогда
как по формуле Симпсона получаем 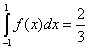 3. Геометрическая иллюстрация
3. Геометрическая иллюстрация
 На отрезке
На отрезке  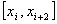 длиной 2h строится парабола, проходящая через три точки
длиной 2h строится парабола, проходящая через три точки 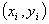 ,
,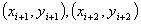 . Площадь под
параболой, заключенная между осью OX и прямыми . Площадь под
параболой, заключенная между осью OX и прямыми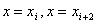 , принимают равной интегралу
, принимают равной интегралу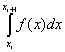 .
Особенностью применения формулы Симпсона является тот факт, что число
разбиений отрезка интегрирования - четное.
Если же количество отрезков разбиения - нечетное, то для первых трех отрезков
следует применить формулу, использующую параболу третьей степени, проходящую
через четыре первые точки, для аппроксимации подынтегральной функции.
.
Особенностью применения формулы Симпсона является тот факт, что число
разбиений отрезка интегрирования - четное.
Если же количество отрезков разбиения - нечетное, то для первых трех отрезков
следует применить формулу, использующую параболу третьей степени, проходящую
через четыре первые точки, для аппроксимации подынтегральной функции.
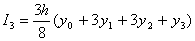 (4)
Это формула Симпсона «трех восьмых».
Для произвольного отрезка интегрирования (4)
Это формула Симпсона «трех восьмых».
Для произвольного отрезка интегрирования 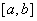 формула (4) может быть «продолжена»; при этом число частичных отрезков должно
быть кратно трем (
формула (4) может быть «продолжена»; при этом число частичных отрезков должно
быть кратно трем (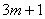 точек).
точек).
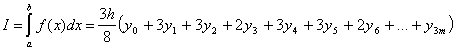
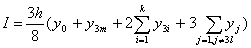 , m=2,3,... (5) , m=2,3,... (5)
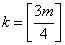 - целая часть
Можно получить формулы Ньютона-Котеса старших порядков : - целая часть
Можно получить формулы Ньютона-Котеса старших порядков :
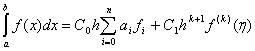 (6) (6)
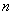 - количество отрезков разбиения; - количество отрезков разбиения;
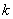 - степень используемого полинома; - степень используемого полинома;
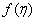 - производная - производная 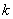 -го порядка в точке -го порядка в точке 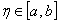 ; ;
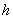 - шаг разбиения.
В таблице 1 выписаны коэффициенты - шаг разбиения.
В таблице 1 выписаны коэффициенты 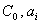 . Каждая строка соответствует одному набору
. Каждая строка соответствует одному набору 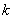 промежутков
промежутков 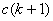 узлами
для построения многочлена k-ой степени. Чтобы воспользоваться этой схемой для
большего количества наборов (например, при k=2 и n=6), нужно «продолжить»
коэффициенты, а затем сложить их.
Таблица 1: узлами
для построения многочлена k-ой степени. Чтобы воспользоваться этой схемой для
большего количества наборов (например, при k=2 и n=6), нужно «продолжить»
коэффициенты, а затем сложить их.
Таблица 1:
| k | C0 | A0 | a1 | a2 | a3 | a4 | a5 | a6 | | | 2 | 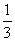
| 1 | 4 | 1 | | | | | | | | | | 1 | 4 | 1 | | | | | | | | | | 1 | 4 | 1 | | | | 1 | 4 | 2 | | 2 | 4 | 1 | å |
Страницы: 1, 2, 3
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



