	Информационно-образоательный портал
	Рефераты, курсовые, дипломы, научные работы,



МЕНЮ\|

поиск

Курсовая: Быстрые вычисления с целыми числами и полиномами

Министерство образования Российской Федерации Ярославский Государственный Университет им. П.Г. Демидова

Курсовая работа

По дисциплине «Алгебра»

Быстрые вычисления с целыми числами и полиномами

Выполнил: Студент группы КБ-11 Сбоев А.В. Проверил: Дурнев В.Г.

Ярославль, 2003 Содержание

1. Введение. Сложность теоретико-числовых алгоритмов. 2. Полиномиальные алгоритмы 2.1 Алгоритм вычисления ad mod m 2.2 Дихотомический алгоритм возведения в степень 2.3 Алгоритм Евклида 2.4 Алгоритм решения уравнения ax + by = 1 3. Полиномиальная арифметика 3.1 Алгоритм нахождения делителей многочлена f(x) в кольце Fp[x] 3.2 Произведение и возведение в степень многочленов, заданных массивами 3.3 Небольшие оптимизации для произведения многочленов 3.4 Вычисление полиномов 3.4.1 Схема Горнера 3.4.2 Интерполяционная формула Ньютона и табулирование значений многочлена 4. Дискретное логарифмирование

1. Введение. Сложность теоретико-числовых алгоритмов

Сложность алгоритмов теории чисел обычно принято измерять количеством арифметических операций (сложений, вычитаний, умножений и делений с остатком), необходимых для выполнения всех действий, предписанных алгоритмом. Впрочем, это определение не учитывает величины чисел, участвующих в вычислениях. Ясно, что перемножить два стозначных числа значительно сложнее, чем два однозначных, хотя при этом и в том, и в другом случае выполняется лишь одна арифметическая операция. Поэтому иногда учитывают ещё и величину чисел, сводя дело к так называемым побитовым операциям, т. е. Оценивая количество необходимых операций с цифрами 0 и 1, в двоичной записи чисел. Это зависит от рассматриваемой задачи, целей автора и т. д. На первый взгляд странным также кажется, что операции умножения и деления приравниваются по сложности к операциям сложения и вычитания. Житейский опыт подсказывает, что умножать числа значительно сложнее, чем складывать их. В действительности же, вычисления можно организовать так, что на умножение или деление больших чисел понадобится не намного меньше битовых операций, чем на сложение. Существует алгоритм Шенхаге – Штрассена, основанный на так называемом быстром преобразовании Фурье, и требующий O(n ln n lnln n) битовых операций для умножения двух n-разрядных двоичных чисел. Таким же количеством битовых операций можно обойтись при выполнении деления с остатком двух двоичных чисел, записываемых не более чем n цифрами. Для сравнения отметим, что сложение n-разрядных двоичных чисел требует O(n ) битовых операций. Говоря о сложности алгоритмов, мы будем иметь в виду количество арифметических операций. При построении эффективных алгоритмов и обсуждении верхних оценок сложности обычно хватает интуитивных понятий той области математики, которой принадлежит алгоритм. Формализация же этих понятий требуется лишь тогда, когда речь идёт об отсутствии алгоритма или доказательстве нижних оценок сложности.

2. Полиномиальные алгоритмы

Четыре приведённых ниже алгоритма относятся к разряду так называемых полиномиальных алгоритмов. Это название носят алгоритмы, сложность которых оценивается сверху степенным образом в зависимости от длины записи входящих чисел. Если наибольшее из чисел, подаваемых на вход алгоритма, не превосходит m, то сложность алгоритмов этого типа оценивается величиной O(ln cm), где c – некоторая абсолютная постоянная. Во всех приведённых примерах с =1. Следующий алгоритм вычисляет admod m. При этом, конечно, предполагается, что натуральные числа a и d не превосходят по величине m. 2.1 Алгоритм вычисления ad mod m 1. Представим d в двоичной системе счисления d = d0 2r+.+dr-12+dr, где di, цифры в двоичном представлении, равны 0 или 1, d0 = 1. 2. Положим a0 = a и затем для i = 1,.,r вычислим ai º a2i-1adi (mod m). 3. ar есть искомый вычет admod m.

Справедливость этого алгоритма вытекает из сравнения

ai º a2i-1ad02^i+.+di (mod m),

легко доказываемого индукцией по i. Так как каждое вычисление на шаге 2 требует не более трёх умножений по модулю m и этот шаг выполняется r £ log2 m раз, то сложность алгоритма может быть оценена величиной O(ln m). 2.2 Дихотомический алгоритм возведения в степень. В общем виде дихотомический алгоритм позволяет вычислить n–ю степень в моноиде. Будучи применён к множеству целых чисел с операцией сложения, этот метод позволяет умножать два целых числа и более известен как египетское умножение. Классический алгоритм возведения в степень посредством последовательного умножения характерен, главным образом, своей неэффективностью в обычных обстоятельствах – его время работы линейным образом зависит от показателя степени. Курсовая: Быстрые вычисления с целыми числами и полиномами

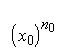Возьмём моноид М с операцией умножения и рассмотрим некоторый элемент x0 из М, а также произвольное натуральное число n0. Для того, чтобы вычислить , представим n0 в двоичной системе счисления: n0 = bt2t + bt – 12t – 1 + . + b121 + b020, предполагая, что n0 содержит (t + 1)двоичных цифр (т. е. что bt ¹ 0 и bt + 1 = 0). В этих условиях вычисляемое выражение может быть записано:

или же . Курсовая: Быстрые вычисления с целыми числами и полиномами

Блок-схема: процесс: function DExp(x, n: LongInt): LongInt;
label 25, 99;
var c: LongInt;
begin
if n mod 2 ¹ 0 then
c : = x
else
c : = 1;
25: n : = n div 2;
if n = 0 then
goto 99;
x:= x*x;
if n mod 2 ¹ 0 then
c : = c*x;
goto 25;
99: DExp : = c;
end;

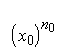
Если задана последовательность (xi)0 £ i £ t, первый элемент которой есть x0 и xi для iÎ [1,t] определено соотношением xi = xi – 12, то можно записать = Pxi . Чтобы завершить построение алгоритма и иметь возможность получить значение предыдущего произведения, необходимо вычислить биты bi числа n0. Для последовательности (ni) 0 £ i £ t+1 (с начальным элементом n0), определённой соотношением n i = [ni–1/2] для любого i Î [1, t + 1], бит bi равен нулю, если n i чётно, и равен единице в противном случае. Первое значение индекса i, для которого ni равно нулю, есть t + 1. Ясно, что число итераций, необходимых для выполнения алгоритма, зависит только от показателя n. 2t £ n £ 2t + 1 или t £ log2n < t + 1. Первая часть этого свойства может быть выражена следующим образом: [n/2 t + 1] = 0 и [n/2t] ¹ 0, что позволяет точно определить число совершаемых делений n, равное числу итераций алгоритма при заданном значении n. Очевидно, нужно совершить t + 1 итераций, чтобы выполнить алгоритм, т. е. [log 2n] + 1 итераций. Следовательно, трудоёмкость алгоритма есть O (log n). Третий алгоритм – это классический алгоритм Евклида вычисления наибольшего общего делителя целых чисел. Мы предполагаем заданными два натуральных числа a и b и вычисляем их наибольший общий делитель (a,b). 2.3 Алгоритм Евклида 1. Вычислим r – остаток от деления числа a на b, a = bq+r, 0 £ r < b. 2. Если r = 0, то b есть искомое число. 3. Если r ¹ 0, то заменим пару чисел (a,b) парой (b,r) и перейдём к шагу1. Не останавливаясь на объяснении, почему алгоритм действительно находит (a ,b), докажем некоторую оценку его сложности. Теорема 1. При вычислении наибольшего общего делителя (a,b) с помощью алгоритма Евклида будет выполнено не более 5p операций деления с остатком, где p есть количество цифр в десятичной записи меньшего из чисел a и b. Доказательство. Положим r0 = a > b и определим r1,r2,.,rn - последовательность делителей, появляющихся в процессе выполнения шага 1 алгоритма Евклида. Тогда r1 = b,., 0 £ ri+1 < ri, i = 0,1,.,n - 1. Пусть также u0 = 1, u1 = 1, uk +1 = uk+uk-1, k ³ 1, - последовательность Фибоначчи. Индукцией по i от i = n - 1 до i = 0 легко доказывается неравенство ri +1 ³ un-i. А так как un ³ 10(n-1)/5, то имеем неравенства 10p > b = r1 ³ un ³ 10(n-1)/5 и n < 5p+1. Немного подправив алгоритм Евклида, можно достаточно быстро решать сравнения ax º 1 (mod m) при условии, что (a,b) = 1. Эта задача равносильна поиску целых решений уравнения ax + by = 1.

2.4 Алгоритм решения уравнения ax + by = 1 0. Определим матрицу E = 1. Вычислим r – остаток от деления числа a на b, a = bq + r, 0 £ r < b. 2.

Если r = 0, то второй столбец матрицы Е даёт вектор (x y) решений уравнения. 3. Если r ¹ 0, то заменим матрицу Е матрицей 4. Заменим пару чисел (a,b) парой (b,r) и перейдём к шагу 1. Если обозначить через Еk матрицу Е, возникающую в процессе работы алгоритма перед шагом 2 после k делений с остатком (шаг 1), то в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное равенство (a,b)*Ek = ( rk-1,rk). Его легко доказать индукцией по k. Поскольку числа a и b взаимно просты, имеем rn = 1, и это доказывает, что алгоритм действительно даёт решение уравнения ax + by = 1. Буквой n мы обозначили количество делений с остатком, которое в точности такое же, как и в алгоритме Евклида. Полиномиальные алгоритмы в теории чисел – большая редкость. Да и оценки сложности алгоритмов чаще всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической теории чисел. Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях всё же можно предложить последовательность действий, которая, «если повезёт», быстро приводит к требуемому результату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную оценку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших оценок сложности.

3. Полиномиальная арифметика

Рассмотрим вероятностный алгоритм, позволяющий эффективно находить решения полиномиальных сравнений по простому модулю. Пусть p – простое число, которое предполагается большим, и f(x)ÎZ[x] – многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения f(x) º 0 (mod p). (1) Например, речь может идти о решении квадратичных сравнений, если степень многочлена f(x) равна 2. Другими словами, мы должны отыскать в поле Fp = Z/pZ все элементы, удовлетворяющие уравнению f(x) = 0. Согласно малой теореме Ферма, все элементы поля Fp являются однократными корнями многочлена xp - x. Поэтому, вычислив наибольший общий делитель d(x) = (xp - x, f(x)), мы найдём многочлен d(x), множество корней которого в поле Fp совпадает с множеством корней многочлена f(x), причём все эти корни однократны. Если окажется, что многочлен d(x) имеет нулевую степень, т. е. лежит в поле Fp, это будет означать, что сравнение (1) не имеет решений. Для вычисления многочлена d(x) удобно сначала вычислить многочлен c(x)ºxp (mod f(x)), пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число p предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить d(x) = (c(x) – x , f(x)). Всё это выполняется за полиномиальное количество арифметических операций. Таким образом, обсуждая далее задачу нахождения решений сравнения (1) мы можем предполагать, что в кольце многочленов Fp[x] справедливо равенство f(x) = (x – a1)*.*(x – an), aiÎFp, ai ¹ aj. 3. 1 Алгоритм нахождения делителей многочлена f(x) в кольце Fp[x] 1. Выберем каким-либо способом элемент d Î Fp. 2. Вычислим наибольший общий делитель g(x) = ( f(x), (x + d)(p-1)/2 – 1). 3. Если многочлен g(x) окажется собственным делителем f (x), то многочлен f(x) распадается на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена f(x). 4. Если окажется, что g(x) = 1 или g(x) = f(x), следует перейти к шагу 1 и, выбрав новое значение d, продолжить выполнение алгоритма. Количество операций на шаге 2 оценивается величиной O(ln p), если вычисления проводить так, как это указывалось выше при нахождении d (x). Выясним теперь, сколь долго придётся выбирать числа d, пока на шаге 2 не будет найден собственный делитель f(x). Количество решений уравнения (t + a1)( p – 1)/2 = (t + a2)( p – 1)/2 в поле Fp не превосходит (p -3)/2. Это означает, что подмножество D Ì Fp, состоящее из элементов d, удовлетворяющих условиям (d + a1)(p – 1)/ 2 ¹ (d + a2)(p – 1)/ 2, d ¹ -a1, d ¹ -a2, состоит не менее чем (p – 1)/2 из элементов. Учитывая теперь, что каждый ненулевой элемент bÎFp удовлетворяет одному из равенств b(p – 1)/2 = 1, либо b(p – 1)/2 = –1, заключаем, что для d Î D одно из чисел a1, a2 будет корнем многочлена (x + d) (p – 1)/2 – 1, а другое – нет. Для таких элементов d многочлен, определённый на шаге 2 алгоритма, будет собственным делителем многочлена f (x). Итак, существует не менее (p –1)/2 «удачных» выборов элемента d, при которых на шаге 2 алгоритма многочлен f(x) распадается на два собственных множителя. Следовательно, при «случайном» выборе элемента d Î Fp, вероятность того, что многочлен не разложится на множители после k повторений шагов алгоритма 1-4, не превосходит 2 -k. Вероятность с ростом k убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно. Заметим, что при оценке вероятности мы использовали только два корня многочлена f(x). При n > 2 эта вероятность, конечно, ещё меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена f(x) не распасться на множители при однократном проходе шагов алгоритма 1-4 не превосходит 2- n + O(p-1/2). Здесь постоянная в O (.) зависит от n. В настоящее время известно элементарное доказательство оценки А. Вейля. Если в сравнении (1) заменить простой модуль p составным модулем m , то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (1) по простым модулям – делителям m, и, следовательно, они требуют разложения числа m на простые сомножители, что, как уже указывалось, является достаточно трудоёмкой задачей. 3.2 Произведение и возведение в степень многочленов, заданных массивами Условимся представлять многочлены массивами, индексированными, начиная с 0, в которых элемент с индексом i означает коэффициент многочлена степени i type Polynome=array[1..Nmax] of Ring_Element; Следующий алгоритм даёт функцию умножения двух многочленов и , где многочлен степени (который даёт результат в конце алгоритма) должен быть предварительно инициализирован нулём. for i:= 0 to degP do for j:= 0 to degQ do R[i+j]:=R[i+j]+P[i]*Q[i]; Изучая предыдущий алгоритм, устанавливаем, что его сложность как по числу перемножений, так и сложений, равна произведению высот двух многочленов: (deg P + 1)(degQ + 1), но в этом алгоритме, который не учитывает случай нулевых коэффициентов, можно рассматривать высоту многочлена как число всех коэффициентов. Значит, возможно улучшить предыдущий алгоритм, исключив все ненужные перемножения: for i:= 0 to degP do if P[i] ¹ 0 then for j:= 0 to degQ do if Q[j] ¹ 0 then R[i+j]:=R[i+j]+P[i]Q[i]; Очень просто вычислить сложность алгоритма возведения в степень последовательными умножениями, если заметить, что когда P – многочлен степени d, то Pi – многочлен степени id. Если обозначить Cmul(n) сложность вычисления P n, то рекуррентное соотношение Cmul(i + 1) = Cmul(i) + (d +1)(id +1) даёт нам:

Страницы: 1, 2

© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент.