|
|
| Курсовая: Математическая теория захватывания |
Курсовая: Математическая теория захватывания
Введение и краткое резюме
Настоящая работа посвящена исследованию движений автоколебаний системы с
одной степенью свободы под действием внешней периодической силы. Такие
движения представляют интерес для радиотелеграфии (например, к исследованию
таких движений сводится теория регенеративного приемника). Особенно
замечательно здесь явления так называемого "захватывания". Это явление
заключается в том, что, когда период внешней силы достаточно близок к периоду
автоколебаний системы, биения пропадают; внешняя сила как бы "захватывает"
автоколебания. Колебания системы начинают совершаться с периодом внешнего
сигнала, хотя их амплитуда весьма сильно зависит от амплитуды "исчезнувших"
автоколебаний. Интервал захватывания зависит от интенсивности сигнала и от
автоколебательной системы.
Теоретически этот вопрос уже разбирался, однако методами математически
недостаточно строгими; кроме того, бралась характеристика весьма частного
вида - кубическая парабола. Поэтому мы будем рассматривать случай
произвольной характеристики при колебаниях близких к синусоидальных.
В этой работе мы рассмотрим периодические решения с периодом, равным периоду
внешней силы, и их устойчивость при малых отклонениях. Мы оставим в стороне
другие стационарные движения, возможные в исследуемой системы, например
периодические решения с периодом, кратным периоду внешней силе, или
квазипериодические решения. Мы оставим в стороне важный вопрос об
устойчивости при больших отклонениях
Для отыскания периодических решений воспользуемся методом Пуанкаре, которые
позволяют быстро решить задачу для случая колебаний, достаточно близких к
синусоидальным. С этой целью введем в наше уравнение параметр m таким
образом, чтобы при m = 0 уравнение превращалось в линейное и колебания
делались синусоидальными. Этот параметр m, который мы предполагать достаточно
малым, может иметь различный смысл в зависимости от выбора системы.
Для решения вопроса об устойчивости найденного решения при малых отклонениях
воспользуемся методами Ляпунова, требуя, чтобы искомые решения обладали
"устойчивостью по Ляпунову".
В настоящей работе мы не будем вычислять радиусы сходимости тех рядов, с
которыми нам придется иметь дело; грубая оценка может быть сделана по
Пуанкаре.
В § 1 и 2 рассматривается область достаточно сильной расстройки; § 3 и 4
посвящены рассмотрению области резонанса; в § 5 показывается, как общие
формулы для амплитуд и для устойчивости, полученные в § 1- 4, могут быть
применены в конкретных случаях, причем в качестве примера рассматривается
случай Ван дер Поля. Результаты применения общих формул совпадают с теми,
которые получил нестрогим путем Ван дер Поль.
§ 1 Отыскание периодического решения в случае достаточно сильной расстройки.
Уравнение, которое нас будет интересовать:
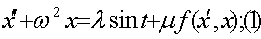 При m = 0 это уравнение имеет единственное периодическое решение
При m = 0 это уравнение имеет единственное периодическое решение
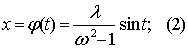 Рассмотрим случай, когда m бесконечно мало. Согласно Пуанкаре мы будем
искать решение (1) в следующем виде:
Рассмотрим случай, когда m бесконечно мало. Согласно Пуанкаре мы будем
искать решение (1) в следующем виде:
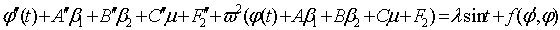
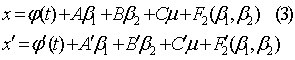 Начальные условия выберем так:
Начальные условия выберем так:
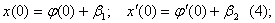 F2 - степенной ряд по b1 b2, m начинающийся с
членов второго порядка. Подставим (3) в (1):
Сравнивая коэффициенты при b1 b2, m получим уравнение
для А, В, С. Начальные условия можно получить для них, подставив (4) в (3).
F2 - степенной ряд по b1 b2, m начинающийся с
членов второго порядка. Подставим (3) в (1):
Сравнивая коэффициенты при b1 b2, m получим уравнение
для А, В, С. Начальные условия можно получить для них, подставив (4) в (3).
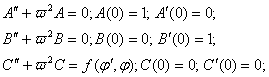 Решая задачи Коши, получим:
Решая задачи Коши, получим:
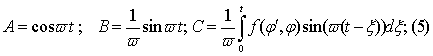 Для того, чтобы (3) представляли периодические решения необходимо и достаточно,
чтобы
Для того, чтобы (3) представляли периодические решения необходимо и достаточно,
чтобы 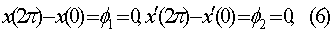 Введем обозначения
Введем обозначения 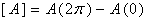 ; для остальных функций аналогично.
Тогда (6) запишется в виде: ; для остальных функций аналогично.
Тогда (6) запишется в виде:
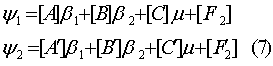 Если в этой системе можно b1 b2 представить в виде
функции m так, чтобы b1 b2, m исчезли из системы (7) ,
то (3) - периодическое решение уравнения (1). Иначе Х- не периодично.
Достаточным условием существования периодического решения при малых m служит
неравенство 0 Якобиана.
В нашем случае:
Если в этой системе можно b1 b2 представить в виде
функции m так, чтобы b1 b2, m исчезли из системы (7) ,
то (3) - периодическое решение уравнения (1). Иначе Х- не периодично.
Достаточным условием существования периодического решения при малых m служит
неравенство 0 Якобиана.
В нашем случае: 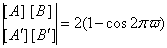 Т.е. мы всегда имеем периодические решения при малых m и любых f. Искомое
периодическое решение может быть найдено в виде.
Т.е. мы всегда имеем периодические решения при малых m и любых f. Искомое
периодическое решение может быть найдено в виде.
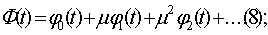 § 2 Исследование устойчивости периодического решения
Составим уравнения первого приближения, порождаемое решением (8). Сделаем
замену: x = Ф(t) + x ; в уравнении (1) при этом отбросим члены , содержащие
квадраты и высшие степени x и x'.
Воспользуемся тем фактом, что Ф (t) - решение уравнения. Получим уравнение
первого приближения:
Это линейное дифференциальное уравнение с периодическими коэффициентами. Его
решение мы будем искать в виде
§ 2 Исследование устойчивости периодического решения
Составим уравнения первого приближения, порождаемое решением (8). Сделаем
замену: x = Ф(t) + x ; в уравнении (1) при этом отбросим члены , содержащие
квадраты и высшие степени x и x'.
Воспользуемся тем фактом, что Ф (t) - решение уравнения. Получим уравнение
первого приближения:
Это линейное дифференциальное уравнение с периодическими коэффициентами. Его
решение мы будем искать в виде 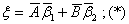 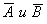 функции времени
функции времени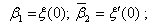 Удовлетворяют тому же уравнению, что и x, то есть (10). Начальные условия для
них определены следующим образом.
Удовлетворяют тому же уравнению, что и x, то есть (10). Начальные условия для
них определены следующим образом.
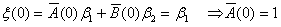 ; аналогичным образом можно показать, что ; аналогичным образом можно показать, что 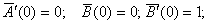 (11).
Представим правую часть уравнения в виде степенного ряда по m. (11).
Представим правую часть уравнения в виде степенного ряда по m.
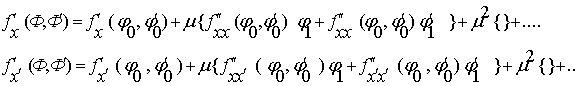
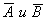 будем искать в виде: будем искать в виде: 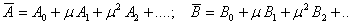 (12).
Подставим (12) в (10) и сравнивая коэффициенты при соответствующих степенях
m, получим:
Начальные условия для Ао , Во, .. Следует выбрать так,
чтобы выполнялись условия (11). Действительно подставляя (11) в (12) и
сравнивая коэффициенты при соответствующих степенях m, получим (12).
Подставим (12) в (10) и сравнивая коэффициенты при соответствующих степенях
m, получим:
Начальные условия для Ао , Во, .. Следует выбрать так,
чтобы выполнялись условия (11). Действительно подставляя (11) в (12) и
сравнивая коэффициенты при соответствующих степенях m, получим
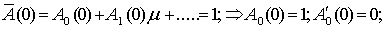 Для В'о и Во аналогично. Для остальных же как
видно из уравнений условия будут нулевые. Итак:
Для В'о и Во аналогично. Для остальных же как
видно из уравнений условия будут нулевые. Итак:
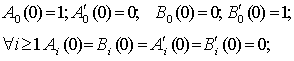 (14)
Решение (13) можно найти при помощи квадратур: (14)
Решение (13) можно найти при помощи квадратур:
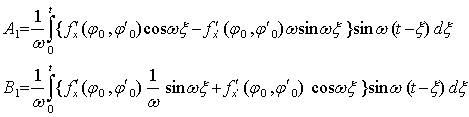 (15)
Если вспомнить общую теорию линейных диффуров с периодическими
коэффициентами, то общее решение (10) имеет вид:
(15)
Если вспомнить общую теорию линейных диффуров с периодическими
коэффициентами, то общее решение (10) имеет вид:
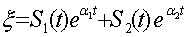 S1, S2 - периодические функции с тем же периодом, что и Ф
(t). a1, a2 - характеристические показатели.
Если все
S1, S2 - периодические функции с тем же периодом, что и Ф
(t). a1, a2 - характеристические показатели.
Если все 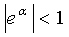 ,
т.е. колебания затухают, то в этом случае выполняется теорема, доказанная
Ляпуновым, относительно того, что периодическое решение уравнения первого
приближения вполне устойчиво. Согласно Пуанкаре характеристические показатели
можно определить из следующего уравнения: ,
т.е. колебания затухают, то в этом случае выполняется теорема, доказанная
Ляпуновым, относительно того, что периодическое решение уравнения первого
приближения вполне устойчиво. Согласно Пуанкаре характеристические показатели
можно определить из следующего уравнения:
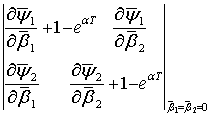 =0 (16) Полагаем =0 (16) Полагаем 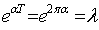 ; ;
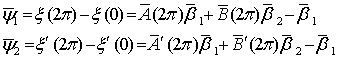 Тогда определитель будет:
Тогда определитель будет:
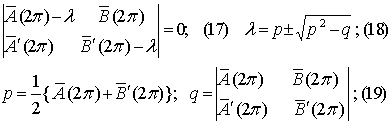 Вопрос об устойчивости, как сказано выше, решается знаком Re (a),
или что все равно ÷ l÷ . Если ÷ l÷ < 1 имеет
место устойчивость ÷ l÷ = 1 этот случай для нашей задачи не
представляет интереса. ÷ l÷> 1 имеет место неустойчивость.
При рассмотрении (18) имеют место 2 случая q > р2; q < р2
; В первом случае l-комплексные; ½l2 ½=q; (20) если
q<1; устойчивость q>1 - неустойчивость.
Случай второй - l - действительные:
Вопрос об устойчивости, как сказано выше, решается знаком Re (a),
или что все равно ÷ l÷ . Если ÷ l÷ < 1 имеет
место устойчивость ÷ l÷ = 1 этот случай для нашей задачи не
представляет интереса. ÷ l÷> 1 имеет место неустойчивость.
При рассмотрении (18) имеют место 2 случая q > р2; q < р2
; В первом случае l-комплексные; ½l2 ½=q; (20) если
q<1; устойчивость q>1 - неустойчивость.
Случай второй - l - действительные: 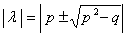 ; (21) устойчивость соответствует
; (21) устойчивость соответствует 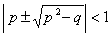 p и q нетрудно получить в виде рядов по степени m из формул (19) (12).
p и q нетрудно получить в виде рядов по степени m из формул (19) (12).
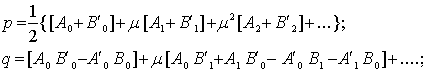 (22)
Если принять во внимание (15)
(22)
Если принять во внимание (15)
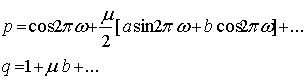 (22a) (22a)
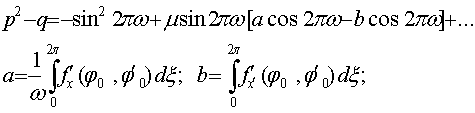 (23)
Мы видим, что при достаточно малом m и w¹n; n ' Z вопрос об устойчивости
решается величиной q и следовательно знаком b, если b < 0- имеет место
устойчивость, b > 0 - неустойчивость.
В нашем случае b имеет вид:
(23)
Мы видим, что при достаточно малом m и w¹n; n ' Z вопрос об устойчивости
решается величиной q и следовательно знаком b, если b < 0- имеет место
устойчивость, b > 0 - неустойчивость.
В нашем случае b имеет вид:
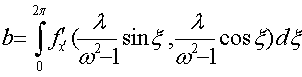 (23a)
§ 3 Отыскание периодического решения в области резонанса.
Тогда l=mlо; w2 = 1+ aо m, (24) (aо
, m - расстройка , реальный физический резонанс наступает при aо
¹ 0).
Тогда исследуемое уравнение имеет вид : (23a)
§ 3 Отыскание периодического решения в области резонанса.
Тогда l=mlо; w2 = 1+ aо m, (24) (aо
, m - расстройка , реальный физический резонанс наступает при aо
¹ 0).
Тогда исследуемое уравнение имеет вид :
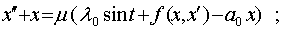 (25)
При m = 0 периодическое решение будет иметь вид : (25)
При m = 0 периодическое решение будет иметь вид : 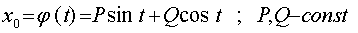 (26)
Следуя Пуанкаре, мы можем предположить периодическое решение в виде: (26)
Следуя Пуанкаре, мы можем предположить периодическое решение в виде:
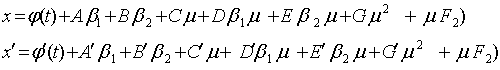 (27);
Начальные условия возьмем как и раньше:
(27);
Начальные условия возьмем как и раньше:
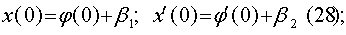 Аналогично тому, как мы это делали в предыдущих параграфах. Подставляем (27) в
(25) и, сравнивая коэффициенты при b1 b2, m и других
интересующих нас величинах, получим уравнение, которым удовлетворяет A, B, C,
D, E, F. Начальные условия для этих уравнений определим, если подставим (28)
в (27).
Аналогично тому, как мы это делали в предыдущих параграфах. Подставляем (27) в
(25) и, сравнивая коэффициенты при b1 b2, m и других
интересующих нас величинах, получим уравнение, которым удовлетворяет A, B, C,
D, E, F. Начальные условия для этих уравнений определим, если подставим (28)
в (27).
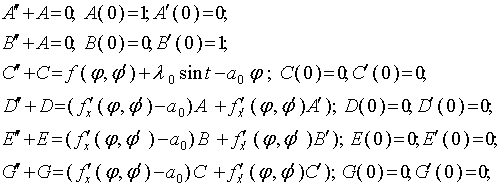 (29)
Запишем условия периодичности для (27):
(29)
Запишем условия периодичности для (27):
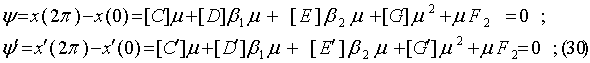 Делим на m:
Делим на m:
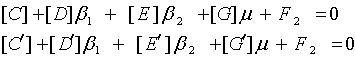 ( 30a )
Необходимым условием существования периодического решения является: ( 30a )
Необходимым условием существования периодического решения является:
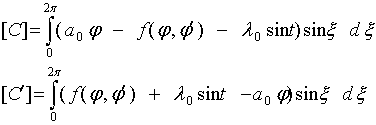 Эти уравнения определяют P и Q решения (26), в близости к которому
устанавливается периодическое решение. Они могут быть записаны в раскрытой
форме :
Эти уравнения определяют P и Q решения (26), в близости к которому
устанавливается периодическое решение. Они могут быть записаны в раскрытой
форме :
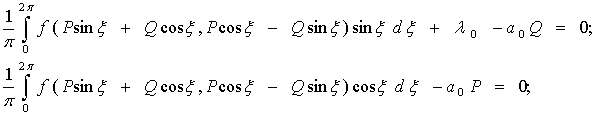 (31)
Для существования искомого периодического решения достаточно неравенство 0
детерминанта: (см. § 1).
(31)
Для существования искомого периодического решения достаточно неравенство 0
детерминанта: (см. § 1).
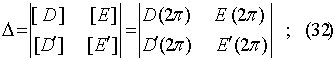 D, Е и их производные найдутся из (29) при помощи формул аналогичных (15).
Заметим, что (30) мы можем определить b1, b2, в виде
рядов по степеням m. Таким образом, мы можем (27) как и в § 1 представить в
виде ряда.
D, Е и их производные найдутся из (29) при помощи формул аналогичных (15).
Заметим, что (30) мы можем определить b1, b2, в виде
рядов по степеням m. Таким образом, мы можем (27) как и в § 1 представить в
виде ряда.
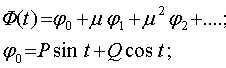 (33)
P,Q-определяются формулами (31) (32).
§ 4 Исследование устойчивости периодических решений в области резонанса
Аналогично тому, как мы это делали в § 2, составим уравнение первого
приближения, порожденное решением (33). (33)
P,Q-определяются формулами (31) (32).
§ 4 Исследование устойчивости периодических решений в области резонанса
Аналогично тому, как мы это делали в § 2, составим уравнение первого
приближения, порожденное решением (33).
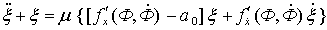 Решение опять будем искать в виде
Решение опять будем искать в виде 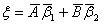 . Однако нет необходимости проделывать все выкладки заново. Воспользуемся
результатами § 2, приняв:
. Однако нет необходимости проделывать все выкладки заново. Воспользуемся
результатами § 2, приняв:
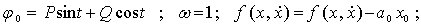 Из формул (22)
Из формул (22) 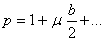 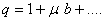 (34) , тогда (34) , тогда 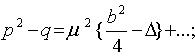 D - тот же Якобиан, что и (32). Распишем его: D - тот же Якобиан, что и (32). Распишем его:
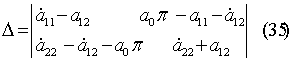
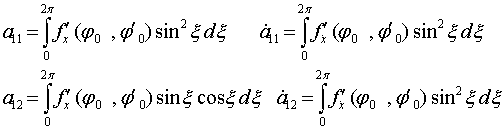 (36)
(36)
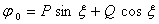 ;
Тогда, зная функцию f, мы можем вычислить D в виде функции P, Q и aо.
Заметим, что равенство (23 а) в нашем случае имеет вид: ;
Тогда, зная функцию f, мы можем вычислить D в виде функции P, Q и aо.
Заметим, что равенство (23 а) в нашем случае имеет вид:
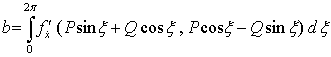 ; (37)
Опираясь на результаты исследования, полученных в § 2, нужно рассмотреть при
исследовании устойчивости два случая: (при достаточно малых m)
1) p2 - q < 0 ; (37)
Опираясь на результаты исследования, полученных в § 2, нужно рассмотреть при
исследовании устойчивости два случая: (при достаточно малых m)
1) p2 - q < 0 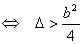 2) p2 - q > 0
2) p2 - q > 0 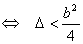 В первом случае устойчивость характеризуется условием q < 1 или, что то же
самое b < 0.
Во втором случае
В первом случае устойчивость характеризуется условием q < 1 или, что то же
самое b < 0.
Во втором случае 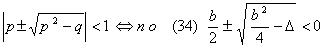 (*) последнее может быть выполнено только, если b < 0, а D > 0. Нетрудно
видеть, что необходимым достаточным условием в обоих случаях является b < 0,
D > 0. (Это можно получить из неравенства (*) ).
§ 5 Применение общих формул, полученных в предыдущих параграфах, к теории
захватывания в регенеративном приемнике для случая, когда характеристика -
кубическая парабола.
Мы рассмотрим простой регенеративный приемник с колебательным контуром в цепи
сетки, на который действует внешняя сила Ро sin w1 t.
Дифференциальное уравнение колебаний данного контура следующее:
(*) последнее может быть выполнено только, если b < 0, а D > 0. Нетрудно
видеть, что необходимым достаточным условием в обоих случаях является b < 0,
D > 0. (Это можно получить из неравенства (*) ).
§ 5 Применение общих формул, полученных в предыдущих параграфах, к теории
захватывания в регенеративном приемнике для случая, когда характеристика -
кубическая парабола.
Мы рассмотрим простой регенеративный приемник с колебательным контуром в цепи
сетки, на который действует внешняя сила Ро sin w1 t.
Дифференциальное уравнение колебаний данного контура следующее:
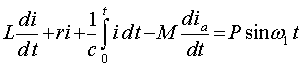 (39)
Считая, что анодный ток зависит только от сеточного напряжения, а также, что
характеристикой является кубическая парабола: (39)
Считая, что анодный ток зависит только от сеточного напряжения, а также, что
характеристикой является кубическая парабола:
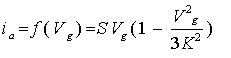 (40)
S-крутизна характеристики, К - напряжение насыщения (40)
S-крутизна характеристики, К - напряжение насыщения 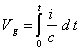 .
Далее, вводя обозначения: .
Далее, вводя обозначения: 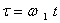
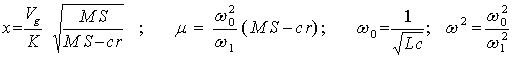 Получим дифференциальное уравнение для х:
Получим дифференциальное уравнение для х:
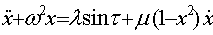 (41)
А: (случай далекий от резонанса).
Для него применяем результаты § 1, полагая (41)
А: (случай далекий от резонанса).
Для него применяем результаты § 1, полагая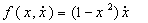 .
Исходное решение в не посредственной близости, к которому устанавливается
искомое решение следующее: .
Исходное решение в не посредственной близости, к которому устанавливается
искомое решение следующее:
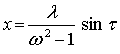 Если w > 1, т.е. wо > w1, то разность фаз равна 0,
если w < 1, то разность фаз равна p. В этом отношении все происходит в
первом приближении также, как и при обычном линейном резонансе. Устойчивость
определяется знаком b (b < 0).
Если w > 1, т.е. wо > w1, то разность фаз равна 0,
если w < 1, то разность фаз равна p. В этом отношении все происходит в
первом приближении также, как и при обычном линейном резонансе. Устойчивость
определяется знаком b (b < 0).
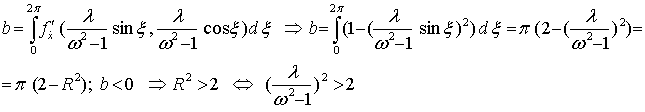 (42).
Т.е. те решения, для которых выполняется это условие, устойчивы.
В: (область резонанса , § 3, 4).
В качестве исходного периодического решения, в непосредственной близости к
которому устанавливается искомое, будет решение следующего вида: x = P sin t
+ Q cos t (P, Q - const).
Запишем уравнение, определяющее эти P и Q, т.е. соотношение (31) для нашего
случая.
(42).
Т.е. те решения, для которых выполняется это условие, устойчивы.
В: (область резонанса , § 3, 4).
В качестве исходного периодического решения, в непосредственной близости к
которому устанавливается искомое, будет решение следующего вида: x = P sin t
+ Q cos t (P, Q - const).
Запишем уравнение, определяющее эти P и Q, т.е. соотношение (31) для нашего
случая.
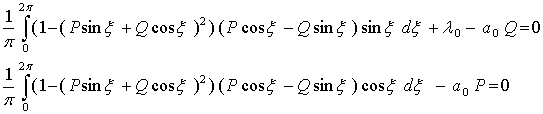 Или преобразовав их, получим следующее:
Или преобразовав их, получим следующее:
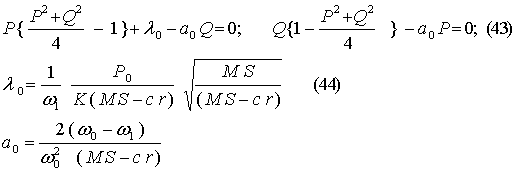 Полагая Р = R sin j; Q = R cos j. Далее найдем для амплитуды R и фазы j для
того исходного периодического решения, в близости к которому
устанавливается рассматриваемое периодическое решение , соотношения
связывающие их :
Полагая Р = R sin j; Q = R cos j. Далее найдем для амплитуды R и фазы j для
того исходного периодического решения, в близости к которому
устанавливается рассматриваемое периодическое решение , соотношения
связывающие их :
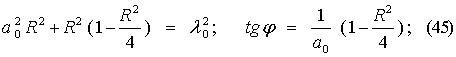 Первая формула дает "резонансную поверхность" для амплитуды. Вторая - для фазы.
По (38) условия устойчивости имеют вид b < 0, D > 0. Считаем b и D
через формулы (35-37).
Первая формула дает "резонансную поверхность" для амплитуды. Вторая - для фазы.
По (38) условия устойчивости имеют вид b < 0, D > 0. Считаем b и D
через формулы (35-37).
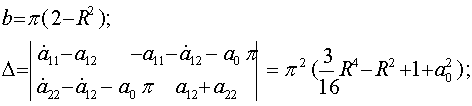 (46)
(46)
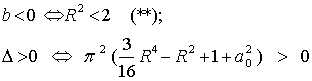 Т.е. решение является устойчивым, если удовлетворяется условие (**). В
заключение выпишем формулы для вычисления aо, соответствующего
ширине захватывания для рассматриваемого случая.
1)
Т.е. решение является устойчивым, если удовлетворяется условие (**). В
заключение выпишем формулы для вычисления aо, соответствующего
ширине захватывания для рассматриваемого случая.
1) 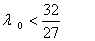 a0 - является общим корнем уравнений
a0 - является общим корнем уравнений
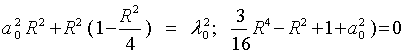 2)
2) 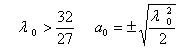 Сама ширина Dw, отсчитанная от одной границы захватывания до другой выражается
следующим образом: Dw = aо w2о (MS - c r).
Можно дать простые формулы для вычисления ширины захватывания в следующих
случаях:
а) l2о << 1; Dw = wо Ро/Vоg.
б) для очень сильных сигналов
Сама ширина Dw, отсчитанная от одной границы захватывания до другой выражается
следующим образом: Dw = aо w2о (MS - c r).
Можно дать простые формулы для вычисления ширины захватывания в следующих
случаях:
а) l2о << 1; Dw = wо Ро/Vоg.
б) для очень сильных сигналов 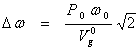 ( Vоg - амплитуда сеточного напряжения при отсутствии
внешней силы).
Список литературы
1. Андронов А.А. Собрание трудов, издательство "Академии наук СССР", 1956.
2. Андронов А.А., Витт А. К теории захватывания Ван дер Поля. . Собрание
трудов, издательство "Академии наук СССР", 1956.
3. Ляпунов А. Общая задача об устойчивости движения, Харьков, 1892.
( Vоg - амплитуда сеточного напряжения при отсутствии
внешней силы).
Список литературы
1. Андронов А.А. Собрание трудов, издательство "Академии наук СССР", 1956.
2. Андронов А.А., Витт А. К теории захватывания Ван дер Поля. . Собрание
трудов, издательство "Академии наук СССР", 1956.
3. Ляпунов А. Общая задача об устойчивости движения, Харьков, 1892.
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



