Каталог Рефератов - Курсовая: Метод итерации - скачать рефераты, бесплатно рефераты

	Информационно-образоательный портал
	Рефераты, курсовые, дипломы, научные работы,



МЕНЮ\|

поиск

Курсовая: Метод итерации

Метод итерации. Если каким-либо способом получено приближенное значение х0 корня уравнения(12.1), то уточнение корня можно осуществить методом последовательных приближений или методом итераций. Для этого уравнение (12.1) представляют в виде: x= (12.6) это уравнение всегда можно решить и притом разными способами, например: x=x+cf(x), (12.7) где с-произвольная постоянная. Пусть число Х1 есть результат подстановки х0 в правую часть уравнения (12.6): Х1= (Х0); далее, Х2= (Х1), Х3= (Х2),.., Хn= (Xn-1) (12.8) Процесс последовательного вычисления чисел Хn (n=1,2,3,.) по формуле (12.8) называется методом последовательных приближений или методом итераций. Итерационный процесс сходится (lim Xn=E), если на отрезке [a,b], содержащем корень Е и его последовательные приближения, выполнено условие maх | (х)|<=q<1. (12.9) Замечание. В качестве Х0 можно взять произвольное значение из интервала, содержащего корень, такой интервал можно сделать достаточно малым. Пример 1. Методом итераций найти меньший положительный корень уравнения: Х-5Х+1=0. Решение. Графически отделяя корни данного уравнения, заключаем, что уравнение имеет три действительных корня, лежащих на отрезках [-3;-2], [0;1],[2; 3]. Найдем меньший положительный корень принадлежащий отрезку [0;1].Укажем отрезок меньшей длины, на котором находится корень. Поскольку f(x)=x-5x+1, f(0)=1>0, f <0, то корень принадлежит отрезку [0;0,5].Данное уравнение приведем к виду (12.6): Х= или X= (X), где . Так как , то условие (12.9) выполнено; процесс итераций будет сходиться. Взяв в качестве начального приближения середину отрезка, т.е. пример Х0=0,25, вычисление последующих приближений проведем по формуле: Хn+1= Результаты этих вычислений представлены в таблице 12.3, из которой видно, что искомый корень Х=0,20164.

n	Xn	xn3	X3n +1	xn+1=(x3n+1)/5
0	0,25	0,01563	1,01563	0,20313
1	0,20313	0,00838	1,00838	0,20168
2	0,20168	0,00821	1,00821	0,20164
3	0,20164	0,00820	1,00820	0,20164

Замечание. При нахождении двух других корней исходного уравнения методом последовательных приближений уже нельзя пользоваться формулой X= (X3+1) , так как max ½j’(x)½ = max 3x2 = 27 >1, 5 2<|x|<3 2<|x|<3 5 5 и условие (12,9) не выполняется. В этом случае данное уравнение следует представить в другом виде, например, Х= ; для функции условие (12,9) на отрезках [-3;-2], [2,3] будет выполняться. Представим выражение f(x)=0 в форме x=Ф(x), что всегда можно сделать разными способами. Выберем на отрезке [a, b] –произвольную точку x0-нулевое приближение. В качестве следующих приближений выберем x1=f(x0 ), x2=f(x1), ., xn=f(xn-1 ). Этот процесс последовательного вычисления чисел xn где (n=1,2,3,.)-называется методом итерации. Процесс итерации следует продолжить до тех пор, пока для двух последующих приближений |xn-x n-1|<=E. Метод отделения корней уравнений. Корнем уравнения f(x)=0 (12.1) называется такое значение х=E аргумента, при котором это уравнение обращается в тождество: f(E)=0. Корень уравнения (12,1) геометрически представляет собой абсциссу точки пересечения, точку касания или другой общей точки графика функции у=f(x) и оси Х (12,1). Курсовая: Метод итерации

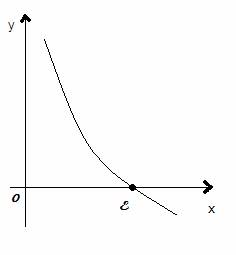
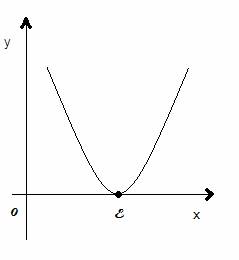
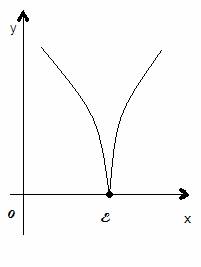Отделить корень уравнения – значит найти такой конечный промежуток, внутри которого имеется единственный корень данного уравнения. Отделение корней можно осуществить аналитическим или графическим способом. Для отделения корней уравнения (12,1) применяют следующий критерий: если на отрезке [a,b] функция f(x) непрерывна и монотонна, а ее значение на концах отрезка имеют разные знаки, то этот отрезок содержит один и только один корень уравнения f(x)=0 , остаточным признаком монотонности f(x) на отрезке является сохранение знака её производной (если f’(x)>0, то функция возрастает; если f’(x)<0, функция убывает). Отделение корней уравнения (12.1) можно выполнить графически, построив график функции f(х), по которому можно судить о том, в каких промежутках находятся точки пересечения его с осью Ох. В некоторых случаях целесообразно представить уравнение (12.1) в эквивалентном виде. f1(x)=f2(x) (12.2) С таким расчетом, чтобы графики функций y1=f1(x) и y2=f2(x) строились проще, чем графики f(x). Корень уравнения (12.2) представляет собой абсциссу точки пересечения графиков y1=f1(x), y2=f2(x). Таким способом можно, например, отделить корни уравнения x3+px+q=0; это будут абсциссы точек пересечения прямой y=-px-q и линии y=x3. Пример 1. Отделить корни уравнения x3+2x-1=0. Решение. В данном случае f(x)=x3+2x-1, f’(x)=3x 2+2. Поскольку f’(x)>0 при всех x, то функция f(x) возрастает в промежутке (-∞,+∞). Корень считается отдельным, если указан конечный промежуток (a,b), на котором он находится. Методом проб находим отрезок [a,b], для которого f(a) f(b)<0 т.е. на концах отрезка функция f(x) принимает значения разных знаков). Для этого вычислим значения функции при некоторых значениях аргумента: f(-1)=(-1)3+2(-1)-1=-4<0, f(0)=-1<0, f(1)=1+2-1=2>0. как f(1) f(0)>0, то на отрезке [-1,0] корня нет; поскольку f(-1) f(0)>0, то корень находится на отрезке [0,1]. Замечание 1. Можно указать отрезок меньшей длины, которому принадлежит корень. Взяв середину отрезка [0,1], т.е. положив x=0,5, по формуле: f(0,5)=(0,5)3+2∙0,5-1>0. Так как f(0) f(0,5)<0, то корень находится на отрезке [0;0,5]. Этот процесс можно продолжать. Замечание 2. Корень данного уравнения можно отделить и графически. Придадим уравнению вид x3=-2x+1, т.е. вид (12.2), и построим графики функций y=x3 , y=-2x+1 (рис. 12.2). Эти графики пересекаются в точке М, абсцисса которой принадлежит интервалу (0,1). Метод касательных. Метод касательных (или метод Ньютона) состоит в следующем. Пусть на отрезке [a,b] находится единственный корень ξ уравнения (12.1). Проведем касательную к кривой y=f(x) в точке A (a, f(a)) до пересечения с осью Ox (рис.12.4): её уравнение имеет вид y f(a)=f’(a) (x-a). Полагая в этом уравнении y=0, находим абсциссу x1 точки пересечения касательной с осью Ox: в предположении, что f’(a)≠ 0.Абсциссу x1 точки пересечения касательной с осью Ox можно взять в качестве x1 -первого приближения корня. Проведя касательную через соответствующую точку A1(x1, f(x1)) и найдя точку её пересечения с осью Ox, получим x2 –второе приближение корня. Аналогично определяются последующие приближения корня. В методе касательных n-ое приближение вычисляется по формуле причем за начальное приближение принимается такое значение х0 из отрезка [a,b] для которого выполняется условие Фурье f(x0 )f ‘’(x)>0 (12.4) Если функция f(x) имеет отличную от нуля производную f ‘(x) на отрезке [a,b], то оценка абсолютной погрешности вычислений определяется формулой (12.5) Пример 1. Методом касательных найти действительный корень уравнения х3+х-3=0. Решение. Записав данное уравнение в виде х3=-х+3 и построив графики функций f1(x)=x3, f2(x) =-x+3,найдем, что единственный корень уравнения принадлежит отрезку [1,2]. Укажем отрезок меньшей длины, на котором находится корень. Так как f(x)=x3 +x-3, f(1,2)=(1,2)3+1,2-3=-0,072<0, f(1,3)=(1,3)3 +1,3-3=0,497>0, то корень лежит на отрезке [1,2;1,2]. Серединой этого отрезка является точка x=1,25. Поскольку f(1,25)=(1,25) 3+1,25-3=0,203125>0 и f(1,2)<0, то искомый корень принадлежит отрезку [1,20;1,25]. Данная функция f(x)=x3 +x-3 имеет производные f ‘(x) =3x2+1, f “(x)=6x, принимающие положительные значения на отрезке [1,20;1,25]. В качестве начального приближения возьмем x=1,25, так как для этой точки выполняется условие (12.4). Результаты вычислений, выполненных по формуле (12.3) записываем в таблице 12.1, из которой видно, что искомый корень x=1,21341.

n	X n Xn	X3n X3n	f(xn )=x3n+xn-3	f’(xn)=3x2n+1	f(xn) f’(xn)	Xn+1=xn= -
0	1,25	1,953125	0, 203125	5,6875	0,035714	1,214286
1	1,214286	1,790452	0,004738	5,42347	0,000874	1,213412
2	1,213412	1,786590	0,000002	5,417107	0,0000004	1,213412

Возьмем некоторую точку x0-отрезка [a, b] и проведем в точке Р0 [x0;f(x0)] - графика функции касательной кривой до пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку Р1[x1;f(x0)] и найдя точки пересечения с осью абсцисс, получим второе приближение корня х 2 и т.д. Затем выводим формулу для последовательных приближений к корню. Уравнение касательной, проходящей через точку Р0, имеет вид : y=f(x)+f(x0)*(x-x0). Полагая, что y=0 найдем абсциссу х 1 – точки пересечения касательной с осью абсцисс х1=x0 ..... .0 Процесс вычисления можно прекратить, если |xn-xn-1|<=E. Метод половинного деления. Уравнение y=f(x), где функция f(x) – непрерывна на отрезке [a, b] и f(a)*f(b)<0. Для нахождения корней уравнения делим отрезок [a, b] пополам, и находим х0=a+b/2. Если при этом f(x)=0, то x0 – является корнем уравнения. Если f(x) неравно 0, то выбираем тот из отрезков [a, b] или [b, x0] имеющие противоположные знаки. Выбранный отрезок снова делим пополам, до тех пор, пока длина отрезка на концах которого 0, не будет меньше заданной точности Е.

© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент.