|
|
| Курсовая: Примеры разностных аппроксимаций |
Курсовая: Примеры разностных аппроксимаций
1. Примеры разностных аппроксимаций.
Различные способы приближенной замены одномерных дифференциальных уравнений
разностными изучались ранее. Напомним примеры разностных аппроксимаций и введем
необходимые обозначения. Будем рассматривать равномерную сетку с шагом h
, т.е. множество точек
wh={xi=ih, i=0, ±1, ±2,.}.
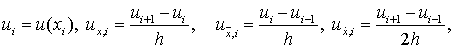 Пусть u(x) – достаточно гладкая функция, заданная на отрезке [xi-1
, xi+1]. Обозначим
Разностные отношения называются соответственно правой,
левой и центральной разностными производными функции u(x) в точке x
i , т.е. при фиксированном xi и при h®0 (тем
самым при i®¥) пределом этих отношений является u’(xi).
Проводя разложение по формуле Тейлора, получим
ux,i – u’(xi) = 0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = -0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = O(h2),
Отсюда видно, что левая и правая разностные производные аппроксимируют u’(x)
с первым порядком по h, а центральная разностная производная – со вторым
порядком. Нетрудно показать, что вторая разностная производная
аппроксимирует u’’(xi) со вторым порядком по h, причем справедливо разложение
Пусть u(x) – достаточно гладкая функция, заданная на отрезке [xi-1
, xi+1]. Обозначим
Разностные отношения называются соответственно правой,
левой и центральной разностными производными функции u(x) в точке x
i , т.е. при фиксированном xi и при h®0 (тем
самым при i®¥) пределом этих отношений является u’(xi).
Проводя разложение по формуле Тейлора, получим
ux,i – u’(xi) = 0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = -0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = O(h2),
Отсюда видно, что левая и правая разностные производные аппроксимируют u’(x)
с первым порядком по h, а центральная разностная производная – со вторым
порядком. Нетрудно показать, что вторая разностная производная
аппроксимирует u’’(xi) со вторым порядком по h, причем справедливо разложение
Рассмотрим дифференциальное выражение
(1)
с переменным коэффициентом k(x). Заменим выражение (1) разностным отношением
(2)
где a=a(x) – функция, определенная на сетке wh. Найдем
условия, которым должна удовлетворять функция a(x) для того, чтобы
отношение (aux)x,i аппроксимировало (ku’)’
в точке xi со вторым порядком по h. Подставляя в (2)
разложения
где ui’ = u’(xi), получим
С другой стороны, Lu = (ku’)’ = ku’’ + k’u’,
т.е.
Отсюда видно, что Lhu–Lu = O(h2), если выполнены условия
(3)
Условия (3) называются достаточными условиями второго порядка аппроксимации
. При их выводе предполагалось, что функция u(x) имеет непрерывную четвертую
производную и k(x) – дифференцируемая функция. Нетрудно показать, что условиям
(3) удовлетворяют, например, следующие функции:
Заметим, что если положить ai = k(xi), то получим только
первый порядок аппроксимации.
В качестве следующего примера рассмотрим разностную аппроксимацию оператора
Лапласа
(4)
Введем на плоскости (x1, x2) прямоугольную сетку с шагом h
1 по направлению x1 и с шагом h2 по направлению x
2, т.е. множество точек
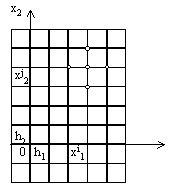 wh = (xi1, xj2) ,
и обозначим
Из предыдущих рассуждений следует, что разностное выражение
(5)
аппроксимирует дифференциальное выражение (4) со вторым порядком, т.е. Lh
uij – Lu(xi1, xj2) = O(h
21) + O(h22). Более того, для функций u(x
1, x2), обладающих непрерывными шестыми производными,
справедливо разложение
Разностное выражение (5) называется пятиточечным разностным оператором
Лапласа, так как оно содержит значения функции u(x1, x2
) в пяти точках сетки, а именно в точках (x1i, x2
j), (x1i±1, x2
j), (x1i, x2 j±
1). Указанное множество точек называется шаблоном разностного оператора.
Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих
большее число точек.
2. Исследование аппроксимации и сходимости
2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась
краевая задача
(k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 < x < l, (1)
– k(0) u’(0) + bu(0) = m1, u(l) = m2, (2)
k(x) ³ c1 > 0, b ³ 0,
для которой интегро-интерполяционным методом была построена разностная схема
(3)
(4)
где
(5)
(6)
Обозначим через Lu(x) левую часть уравнения (1) и через Lh
yi – левую часть уравнения (3), т.е.
Пусть u(x) – достаточно гладкая функция и u(xi) – ее значение в точке xi сетки
wh = {xi = ih, i = 0, 1, .,N, hN = l} (7)
Говорят, что разностный оператор Lh аппроксимирует
дифференциальный оператор L в точке x=xi, если разность
Lhui – Lhu(xi) стремится к нулю
при h®0. В этом случае говорят также, что разностное уравнение (3)
аппроксимирует дифференциальное уравнение (1).
Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора
в точке x=xi значения ui±1
= u(xi ± h), входящие в разностное выражение Lhu
i. Большая часть этой работы проделана в предыдущей главе, где
показано, что при условиях wh = (xi1, xj2) ,
и обозначим
Из предыдущих рассуждений следует, что разностное выражение
(5)
аппроксимирует дифференциальное выражение (4) со вторым порядком, т.е. Lh
uij – Lu(xi1, xj2) = O(h
21) + O(h22). Более того, для функций u(x
1, x2), обладающих непрерывными шестыми производными,
справедливо разложение
Разностное выражение (5) называется пятиточечным разностным оператором
Лапласа, так как оно содержит значения функции u(x1, x2
) в пяти точках сетки, а именно в точках (x1i, x2
j), (x1i±1, x2
j), (x1i, x2 j±
1). Указанное множество точек называется шаблоном разностного оператора.
Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих
большее число точек.
2. Исследование аппроксимации и сходимости
2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась
краевая задача
(k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 < x < l, (1)
– k(0) u’(0) + bu(0) = m1, u(l) = m2, (2)
k(x) ³ c1 > 0, b ³ 0,
для которой интегро-интерполяционным методом была построена разностная схема
(3)
(4)
где
(5)
(6)
Обозначим через Lu(x) левую часть уравнения (1) и через Lh
yi – левую часть уравнения (3), т.е.
Пусть u(x) – достаточно гладкая функция и u(xi) – ее значение в точке xi сетки
wh = {xi = ih, i = 0, 1, .,N, hN = l} (7)
Говорят, что разностный оператор Lh аппроксимирует
дифференциальный оператор L в точке x=xi, если разность
Lhui – Lhu(xi) стремится к нулю
при h®0. В этом случае говорят также, что разностное уравнение (3)
аппроксимирует дифференциальное уравнение (1).
Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора
в точке x=xi значения ui±1
= u(xi ± h), входящие в разностное выражение Lhu
i. Большая часть этой работы проделана в предыдущей главе, где
показано, что при условиях
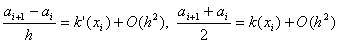 (8)
выполняется соотношение
Если кроме того, докажем, что
di = q(xi) + O(h2), ji = f(xi) + O(h2) (9)
то тем самым будет установлено, что оператор Lh
аппроксимирует L со вторым порядком по h, т.е.
Lhui – Lu(xi) = O(h2), i = 1, 2,., N–1 (10)
Итак, доказательство второго порядка аппроксимации сводится к проверке сводится
к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала
выполнение условий (8). Обозначая p(x) = k-1(x), получим
следовательно,
Аналогично
Отсюда получим
т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена
интегралов (6) значениями qi, fi соответствует
приближенному вычислению этих интегралов по формуле прямоугольников с узлом в
середине отрезка интегрирования.
2.2. Аппроксимация граничного условия. Исследуем погрешность
аппроксимации разностного граничного условия (4). Обозначим lh
u(0) = –a1ux, 0 + bu0. Если u(x) –
произвольная достаточно гладкая функция, то очевидно
lhu(0) = –k(0) u’(0) + bu(0) + O(h),
т.е. имеет место аппроксимация первого порядка по h. Однако если
u=u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет
второй порядок аппроксимации, т.е. (8)
выполняется соотношение
Если кроме того, докажем, что
di = q(xi) + O(h2), ji = f(xi) + O(h2) (9)
то тем самым будет установлено, что оператор Lh
аппроксимирует L со вторым порядком по h, т.е.
Lhui – Lu(xi) = O(h2), i = 1, 2,., N–1 (10)
Итак, доказательство второго порядка аппроксимации сводится к проверке сводится
к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала
выполнение условий (8). Обозначая p(x) = k-1(x), получим
следовательно,
Аналогично
Отсюда получим
т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена
интегралов (6) значениями qi, fi соответствует
приближенному вычислению этих интегралов по формуле прямоугольников с узлом в
середине отрезка интегрирования.
2.2. Аппроксимация граничного условия. Исследуем погрешность
аппроксимации разностного граничного условия (4). Обозначим lh
u(0) = –a1ux, 0 + bu0. Если u(x) –
произвольная достаточно гладкая функция, то очевидно
lhu(0) = –k(0) u’(0) + bu(0) + O(h),
т.е. имеет место аппроксимация первого порядка по h. Однако если
u=u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет
второй порядок аппроксимации, т.е.
Докажем последнее утверждение. Используя разложение
ux, 0 = (u1 – u0)/h = u’(x1/2) + O(h2), x1/2 = 0,5h,
a1 = k1/2 + O(h2)
получим
Страницы: 1, 2, 3
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



