Курсовая: Сравнительный анализ алгоритмов построения выпуклой оболочки на плоскости

Сравнительный анализ алгоритмов построения выпуклой оболочки на плоскости

Аннотация

Тема данной курсовой работы – " Сравнительный анализ алгоритмов построения

выпуклой оболочки на плоскости". Для сравнения взяты четыре алгоритма: обход

методом Грэхема, быстрый метод, метод “разделяй и властвуй” и динамический

метод. Задача этой работы – раскрыть эти алгоритмы и провести исследования

эффективности их.

Программная часть для курсовой работы выполнена на Borland Delphi 4.

Оглавление

Аннотация 2

Введение 4

Предварительная разработка алгоритма построения выпуклой оболочки 7

Метод обхода Грэхема 9

Быстрые методы построения выпуклой оболочки. 11

Алгоритмы типа “разделяй и властвуй”. 12

Динамические алгоритмы построения выпуклой оболочки 14

Сравнительный анализ алгоритмов построения выпуклой оболочки 17

Выводы 20

Заключение 21

Приложение Unit1.pas 22

Литература 34

Введение

Множество различных задач вычислительной геометрии связано с построением

выпуклой оболочки. В настоящий момент эта задача хорошо исследована и имеет

широкое применение в распознавании образов[1]

, обработке изображений[2], а так же в

задачах в задаче раскроя и компоновки материала

[3].

Само понятие выпуклой оболочки является довольно простым и интуитивно понятным.

Если представить резиновый шнур, натянутый на множество точек, то это и будет

выпуклая оболочка для данного множества точек. Но, не смотря на свою простоту,

оно не конструктивно, поэтому далее будут рассмотрены способы построения

эффективных алгоритмов для построения выпуклой оболочки. Так как алгоритмы для

решения нашей задачи, как правило, являются подзадачами других, более сложных

задач, то интерес представляют только алгоритмы имеющие сложность O(

N log N).

Само понятие выпуклой оболочки является довольно простым и интуитивно понятным.

Если представить резиновый шнур, натянутый на множество точек, то это и будет

выпуклая оболочка для данного множества точек. Но, не смотря на свою простоту,

оно не конструктивно, поэтому далее будут рассмотрены способы построения

эффективных алгоритмов для построения выпуклой оболочки. Так как алгоритмы для

решения нашей задачи, как правило, являются подзадачами других, более сложных

задач, то интерес представляют только алгоритмы имеющие сложность O(

N log N).

Для начала, несколько определений:

Определение 1. Область D принадлежащая пространству E2

, будет называться выпуклой, если для любой пары точек q1

и q2 из D отрезок q1q2

целиком принадлежит D.

Определение 2. Выпуклой оболочкой множества точек S,

принадлежащих пространству E2, называется граница наименьшей

выпуклой области в E2, которая охватывает S.

Далее будем иметь дело только с множествами, состоящими из конечного числа

точек. Поэтому чтобы охарактеризовать структуру выпуклой оболочки нам нужно

обобщить понятия выпуклого многоугольника.

Определение 3. Полиэдральным множеством или политопом называется

пересечение конечного множества замкнутых полупространств.

Следующая теорема характеризует выпуклые оболочки в нужном нам плане.

Теорема 1[4]. Выпуклая

конечного множества точек.

Прежде чем переходить к описанию алгоритмов следует произвести постановку задач

и определить нижние оценки для решения их. Так как алгоритмы имеют дело с

границей выпуклой оболочки множества L conv(L), то введем для

нее обозначение CH(L) и будем ее также называть выпуклой оболочкой.

Сформулируем две основные задачи:

Задача ВО1. (Выпуклая оболочка). В E2 задано множество

S, содержащее N точек. Требуется построить их выпуклую оболочку

(т.е. полное описание границы CH(S)).

Задача ВО2. (Открытый алгоритм для выпуклой оболочки). На плоскости

задана последовательность из N точек p1, ., p

N. Требуется найти выпуклую оболочку таким образом, чтобы, после

обработки точки pi имелась CH({p1, .,

pi}).

Рассмотрим ВО1. То, что вершины многоугольника, являющегося выпуклой

оболочкой, следуют в определенном порядке, указывает на связь с задачей

сортировки. В самом деле, следующая теорема показывает то, что решение ВО1

должно быть в состоянии выполнить сортировку.

Теорема 2. Задача сортировки за линейное время сводится к задаче

выпуклой оболочки для N точек на плоскости требуется время W(N log

N).

Доказательство. Сведем задачу сортировки N положительных

действительных чисел x1,.., xN к задаче

ВО1. Поставим в соответствие числу xi точку (xi

, xi2) и присвоим ей номер i. Выпуклая

оболочка этого множества, представленная в стандартном виде будет представлять

собой упорядоченное относительно значения абсциссы множество всех точек из

исходного. Из него за линейное время можно получить отсортированный список.

Очевидно, что если мы можем решать ВО2, то мы можем решить и ВО1, по-этому

задача ВО1 может быть сведена к ВО2 за линейное время. Следовательно, нижняя

оценка для ВО2 не ниже W(N log N).

Предварительная разработка алгоритма построения выпуклой оболочки

Для начала рассмотрим несколько малопродуктивных алгоритмов построения

выпуклой оболочки.

Определение 3. Точка p выпуклого множества S называется

крайней, если не существует пары точек a, b Î S

таких, что p лежит на открытом отрезке ab.

Очевидно, что подмножество крайних точек E является наименьшим

подмножеством S, выпуклая оболочка которого, является выпуклой

оболочкой множества S, или conv(E)=conv(S). Поэтому нам

необходимо для нахождения выпуклой оболочки выполнить два шага:

Определить крайние точки.

Упорядочить эти точки так, чтобы они образовали выпуклый многоугольник.

Теорема 3. Точка p не является крайней точкой множества S только

S, но сама она не является вершиной этого треугольника.

Эта теорема дает возможность построить алгоритм проверки крайности точки. Если

мы имеем дело с множеством S мощности N, то можно построить

O(N3) треугольников. Проверка принадлежности точки

треугольнику выполняется за постоянное количество операций. Следовательно, за

время O(N3) можно определить, является ли точка

крайней, а за O(N4) и для всех точек.

Следующая теорема показывает, – в каком порядке должны быть точки в конечном

множестве.

Теорема 4. Последовательные вершины выпуклого многоугольника

внутренней точки.

Упорядочить крайние точки множества можно относительно их центроида. Центроид

множества для N точек вычисляется за время O(N)

арифметических операций. Грэхем предложил использовать для этого только три

любые неколлинеарные точки множества S. В худшем случае это требует

время O(N), но почти всегда это первые три точки.

Упорядочить их можно за время O(N log N). Таким образом,

мы решаем задачу ВО1 за время O(N4).

Метод обхода Грэхема

Приведенный выше алгоритм является неэффективным, поэтому необходим способ

более быстрого построения выпуклой оболочки. Для этого нам необходим другой

подход.

Грэхэм в одной из первых своих работ сумел показать, как можно, предварительно

отсортировав точки относительно полярного угла с центром в какой-нибудь

внутренней точке, можно найти крайние точки за линейное время

[5].

Пусть центр координат в какой-нибудь внутренней точке. Упорядочим точки

относительно полярного угла, а если таковые совпадают относительно расстояния

от центра координат. Так как обе точки лежат на одной прямой проходящей через

центр координат, то для сравнения нам нет необходимости вычислять расстояние,

а можно сравнивать сумму абсолютных значений координат.

Отсортированные точки следует поместить в двусвязный список. Так как внутренние

точки принадлежат некоторому треугольнику (Opq), где p и q

– соседние вершины точке выпуклой оболочки. Суть алгоритма в последовательном

просмотре отсортированного списка и удалении внутренних вершин. Оставшиеся

точки будут являться вершинами выпуклой оболочки.

Просмотр начнем с точки являющейся вершиной ВО. Для этого можно взять точку с

минимальной абсциссой, а если их несколько, то и минимальной ординатой и

пометить как начальную. После чего, обходим список, начиная с нее, против

часовой стрелки и проверяем внутренний угол для текущей точки. Если он больше

либо равен p, то удаляем вершину, а иначе переходим к следующей. Так как за

каждый просмотр мы или удаляем одну вершину, или переходим к следующей, а

просмотр заканчиваем при достижении вершины начало, которая не удалится, то мы

выполняем не более N шагов. Рассмотренный метод называют методом

обхода Грэхема.

Теорема 5. Выпуклая оболочка N точек на плоскости может быть найдена

за время O(N log N) при памяти O(N) с

Доказательство. Из предыдущего алгоритма видно, что в нем используются

только арифметические операции и сравнения. Для нахождения внутренней точки и

обхода требуется линейное время, а на сортировку уходит O(N log N). Для

представления списка нам достаточно O(N) памяти.

Так как выше было доказано, что нижняя оценка для алгоритма решающего эту задачу

равна O(N log N), то получаем, что обход Грэхема имеет

оптимальное время выполнения. Но он является оптимальным в худшем случае, а

поведение его в среднем мы не изучили. Этот алгоритм имеет несколько

недостатков.

В нем используются тригонометрические функции, а так как их вычисление связано с

большими затратами по времени, то желательно от них избавиться. Эндрю предложил

метод решения этой проблемы[6].

Если на плоскости заданы N точек, то существует самая левая и самая

правая точки, и они являются вершинами выпуклой оболочки. Прямая, проходящая

через эти точки делит множество на две части. Это точки, которые лежат выше и

точки, которые ниже прямой. Оба множества порождают соответствующие им части

выпуклой оболочки, причем они являются монотонными ломаными относительно оси

x. Поэтому, отдельно отсортировав эти множества по значению абсциссы,

производится обход Грэхема.

Недостатками алгоритма являются и то, что он не открытый, а так же не

допускает разбиение исходной задачи на подзадачи для параллельной обработки.

Быстрые методы построения выпуклой оболочки.

Для построения выпуклой оболочки можно создать алгоритмы построения выпуклой

оболочки, напоминающие быструю сортировку. Такие алгоритмы называются

быстрыми методами построения оболочки.

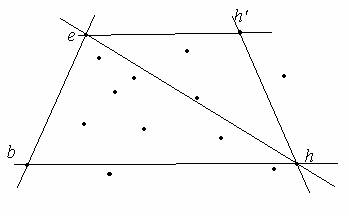
Рис. 1: h – самая удаленная от bl точка.

Суть алгоритма состоит в том, что исходное множество S из N

точек разбивается на два подмножества, каждое из которых будет содержать одну из

Страницы: 1, 2, 3, 4