Лекция: Лекции переходящие в шпоры Алгебра и геометрия

1. Матрицы. Терминология и обозначения.

Матрицей размера (mxn) называется набор m×n чисел – элементов м-цы Ai,j,

записанных в виде прямоугольной таблицы:

Набор аi1, ai2, ain – наз iтой строкой м-цы. Набор a1j, a2j, amj – jтым

столбцом.

М-ца размером 1хп – называется строкой, вектором; м-ца размером mx1 –

столбцом. Если размерность пхп – матрица называется квадратной. Набор

элементов а11, а22, апп образует главную диагональ м-цы. Набор а1п, а1,п-1,

ап1 – побочную диагональ. М-ца все эл-ты, которой = 0 наз. нулевой.

Квадратная м-ца, элементы главной диагонали которой равны 1, а все остальные

– 0, называется единичной, обозн.: Е

Матрицы: А(I,j) и B(I,J) называется равными, если равны их размеры и их

элеме6нты в одинаковых позициях совпадают.

2. Действия с матрицами

1) Сложение

Суммой м-ц А(I,j) и B(I,J) наз. м-ца С(I,J) элементы кот, выч по формуле:

Сij=Aij+Bij (I=1.m, j = 1.n)

C=A+B (размер всех м-ц: mxn)

2) умножение м-цы на число

Произведение м-цы А = (Aij) размера mxn на число С называется матрица:

B=(Bij) размера mxn, элементы кот, выч. по формуле:

Вij=С×Aij (I=1.m, j = 1.n)

В=С×А

вычитание:

С=А+(-)В = А-В

3) умножение м-ц

А=(Aik), B=(Bkj) – квадратные м-цы порядка n. Произведением А на В называют

м-цу С= (Сij) элементы, кот выч. по формуле:

Сij = Ai1×B1j+. Ain×BnJ

С=АВ. Можно записать так:

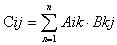
Порядок сомножителей в матрице существенен: АВ не равно ВА

Св-ва умножения м-цы:

(АВ)С=А(ВС)

А(В+С)=АВ+АВ, (А+В)С=АС+ВС

Произведение двух прямоугольных матриц существует, если их внутренние размеры

(число столбцов первой, и число строк второй) равны.

3. Порядки суммирования. Транспонирование м-цы

Сумму Н всех элементов квадратной м-цы А можно вычислить 2 мя способами:

1. Находя сумму элементов каждого столбца и складывая полученные суммы:

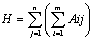
2. Находя сумму элементов каждой строки и складывая эти суммы:

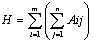
отсюда вытекает, что

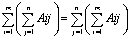
порядок суммирования в двойной сумме можно менять.

Матрица

называется транспонированной по отношению к м-це А=

Обозначается АТ. При транспонировании строки переходят в столбцы, а

столбцы в строки и если А размером mxn, то АТ будет размером nxm

Св-ва операции транспонирования.

1 (АТ)Т=А

2 (А+В)Т=АТ+ВТ

3 (СА)Т=САТ (С-число)

4 (АВ)Т=АТ×ВТ

4. Элементарные преобразования матрицы.

1 Переставление двух строк

2 Умножение строки на не равное 0 число В

3 Прибавление к строке матрицы другой ее строки, умноженной на число С.

Также производят элементарные преобразования столбцов.

5. Матрицы элементарных преобразований.

С элементарными преобразованиями тесно связаны квадратные матрицы

элементарных преобразований. Они бывают следующих типов:

1 м-цы получающиеся из единичных путем перестановки двух любых строк например

м-ца:

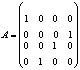получена перестановкой 2 и 4 строки

2 тип. м-цы получающиеся из единичной заменой диагонального элемента на

произвольное не нулевое число:

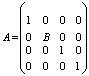
отличается от единичной элементом В во второй строке

3 тип отличающиеся лишь одним недиагональным не нулевым элементом: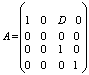

Основное св-во матриц элементарных преобразований Элементарное преобразование

произвольной матрицы равносильно умножению этой м-цы на матрицу элементарных

преобразований

Элементарные преобразования строк м-цы А

1 умножение м-цы А на м-цу 1 типа слева переставляет строки с номерами I,j

2 Умножение м-цы А на м-цу второго типа слева равносильно умножению j строки

м-цы А на число В

3 прибавление к jстороке м-цы А ее iтой строки, умноженной на число С

равносильно умножению м-цы А на м-цу 3 типа слева

Элементарные преобразования столбцов м-цы А

1 умножение м-цы А на м-цу 1 типа справа переставляет столбцы с номерами I,j

2 Умножение м-цы А на м-цу второго типа справа равносильно умножению j

столбца м-цы А на число В.

3 прибавление к j столбцу м-цы А ее I того столбца, умноженного на число С

равносильно умножению м-цы А на м-цу 3 типа справа.

6. Определители

С каждой квадратной матрицей связано некое число наз. определителем.

Определителем м-цы второго порядка:

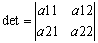
наз число: а11×а22-а12×а21

Определитель м-цы третьего порядка:

=

=

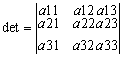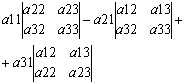
также можно восп правилами треугольника:

Предположив, что определитель м-цы порядка меньше n уже известен,

определитель м-цы порядка n будет равен:

D= a11×M11-a21×M21+.+(-1)n+1×an1×Mn1

где Мi1 – определитель м-цы порядка n-1, это число называется дополнительным

минором. Подобная м-ца получается из А путем вычеркивания 1 столбца и j

строки. Это называется разложением определителя по 1 ому столбцу.

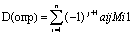
число: Аij=(-1)I+1×Mij называется алгебраическим

дополнением эл-та аij в определителе [А] с учетом алгебр. доп ф-лу нахождения

определителя можно записать так:

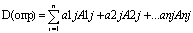
Определитель – сумма попарных произведений эл-тов произвольного столбца на их

алгебраический дополнитель.

1. Свойства определителя

1 При транспонировании матрицы определитель не изменяется: [AT]=[А]

отсюда вытекает, что строка и столбец равноправны с точки зрения свойств

определителя.

2 Линейность

Если в определителе D I является линейной комбинацией 2-х строк:

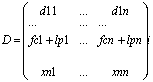
тогда D=fD’+lD’’

где: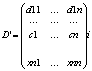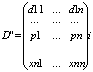

отличаются от D только I-тыми строками.

3 Антисимметричность если определитель В* получен из опр В перестановкой

строк, то В* = -В

4 Определитель матрицы с двумя одинаковыми строками равен 0

5 Умножение строки определителя на число равносильно умножению самого

определителя на это число

6 определитель с 0 строкой = 0

7 определитель, одна из строк которого = произв другой строки на число не

равное 0 = 0. (Число выносится за определитель далее по св-ву 4)

8 Если к строке определителя прибавить другую его строку, умноженную на какое

либо число, то полученный определитель будет равен исходному.

9 Сумма произведения эл-тов строки определителя на алгебр. дополнение

соответствующих элементов другой строки опр = 0

8. Обратная матрица

Квадратная матрица наз. невырожденной, если ее определитель не равен 0.

М-ца В, полученная из невырожд м-цы А по правилу:

В позицию ij м-цы В помещается число = алгебраическому дополнению м-цы Aji,

эл-та аji в м-це А.

М-ца В наз. союзной или присоединенной к м-це А и обладает следующими св-вами:

АВ=ВА=[А]I (I-единичная матрица)

Матрица А-1=1/[А]В называется обратной м-це А. Отсюда вытекает равенство:

АА-1=I, А-1А=I

М-цу А-1 можно рассматривать как решение 2х матричных уравнений АХ=I, ХА=I, где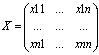

- неизвестная матрица.

Произвольную невырожденную м-цу элементарными преобразованиями строк можно

привести к единичной матрице

1 Привести к треугольному виду

2 Диагональ матрицы преобр 2 вида приводится к равенству единицам

3 Преобразованиями 3 го типа, прибавляя к п-1 строке последнюю умноженную на

–а1п, -а2п.-ап-1п, приводится к матрице у которой все эл-ты п-ного столбца,

кроме последнего равны 0 и т. д.

2 метод построения обратной м-цы путем составления расширенной матрицы (метод

Жордана)

1 составляется расширенная матрица, приписывая к матрице А единичную матрицу

I того же порядка т. е. получаем м-цу (А|I) элементарными преобр строк м-ца А

приводится к треугольному виду, а потом к единичному, полученаая на месте I

м-цы м-цы С – является обратной исходной матрице А

15. Понятия связанного и свободного векторов.

Рассмотрим т А и т. В, по соединяющему их отрезку можно перемещать в двух

направлениях: если считать А началом, а т. В – концем, то получим

направленный отрезок АВ, а если т. В- начало, а т. А – конец, то направленный

отрезок ВА. Направленный отрезок часто наз. связанными или закрепленными

векторами. В случае, когда начальная и конечная точка совпадают, т. е. А=В,

связанный вектор наз. нулевым..

Связанные векторы АВ и СД равны, если середины отрезков АД и ВС совпадают

обоз: АВ=СД, отметим, что в случае, когда т. А,В,С,Д не лежат на одной прямой

это равносильно тому, что четырехугольник АВСД – параллелограмм. Поэтому

равные связанные в-ры имеют равные длины.

Св-ва связанных в-ров:

1 Каждый связанный в-р равен самому себе АВ=АВ

2 Если АВ=СД, то и СД = АВ

3 Если АВ=СД и СД=EF, то AB=EF

От каждой точки можно отложить связанный в-р равный исходному.

Свободные в-ры – те, начальную точку которых можно выбирать произвольно. или,

что тоже самое, которые можно произвольно переносить параллельно самим себе.

Свободный в-р однозначно определяется заданием связанного в-ра АВ.

Обоз свободные в-ры малыми латинскими буквами и стрелкой сверху. Нуль-вектор

обоз 0 со стрелкой.

Если задан в-р а и т. А, сущ ровно 1 т. В, для которых АВ=а. Операция

построения связанного в-ра АВ, для которой выполнено это равенство называется

откладывание свободного в-ра а от т. А. Связанные в-ры, полученные в

результате операции откладывания равны между собой. И имеют одинаковую длину.

Длина свободного в-ра а обоз |f|, длина нуль-в-ра=0, Если а=в, то и длины их

равны., обратное неверно!!!.

16. Линейные операции над в-рами

Страницы: 1, 2, 3