Реферат: Граничные условия общего вида
План.
1. Сопряженный оператор.
2. Сопряженная однородная задача.
3. Условия разрешимости.
Сопряженный оператор.
Обозначим через 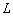 дифференциальный оператор второго порядка, т.е. дифференциальный оператор второго порядка, т.е.
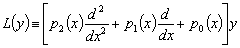 (1) (1)
где 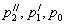 представляют представляют
собой непрерывные функции в промежутке 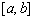
. Если 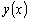 и и 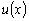
- дважды непрерывно дифференцируемые на 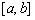
функции, то имеем:
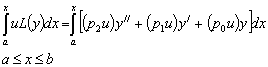 (2) (2)
Как и в предыдущем параграфе, интегрирование соотношения (2) по частям дает:
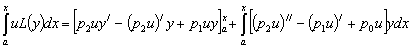
(3)
Обозначим дифференциальный оператор, входящий в подынтегральное выражение в
правой части (3) через 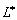
, т.е.
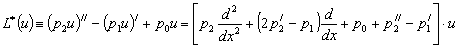
(4)
При этом соотношение (3) перепишется так:
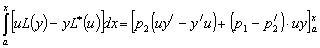 (5) (5)
Оператор 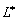 называется называется
сопряженным по отношению к оператору 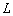
. Умножая соотношение (4) на 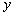
и интегрируя полученный результат по частям, по отношению к оператору 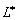
. Таким образом, операторы 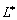
и 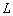 взаимно взаимно
сопряжены.
Как и в предыдущем параграфе, дифференциальное уравнение:
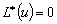 (6) (6)
будем называть сопряженным дифференциальному уравнению:
 (7) (7)
Если же 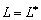 , то , то
оператор 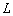 и и
дифференциальное уравнение 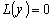
будем называть сопряженными. Сравнивая выражения (1) и (5), приходим к выводу,
что 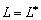 тогда и тогда и
только, когда:
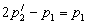
Таким образом, оператор 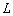 будем самосопряженным тогда и только тогда, когда будем самосопряженным тогда и только тогда, когда 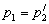 . .
При этом:
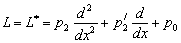
Так как любое дифференциальное уравнение вида (7) можно преобразовать в
самосопряженную форму, умножив на функцию 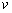
.
Дифференцируя соотношение (5) по 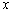 , получаем так называемую формулу Лагранжа: , получаем так называемую формулу Лагранжа:
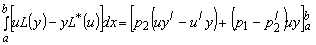 (8) (8)
Правая часть этой формулы может быть записана как:
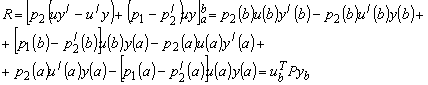
(9)
где
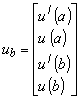 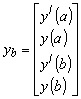 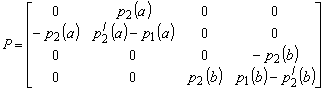 (10) (10)
Отметим, что:
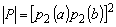 и следовательно, и следовательно,
матрица 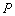
-невырожденная. Подстановка выражения (9) в соотношение (8) дает:
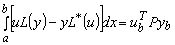 (11) (11)
Сопряженная однородная задача.
Введем следующее невырожденное линейное преобразование 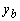 в вектор в вектор 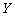 : :
 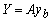 (12), (12),
где
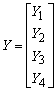 
Заметим, что указанное преобразование может быть выполнено бесчисленным
множеством способов, в зависимости от выбора матрицы А. При заданном ненулевом
векторе 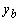 две две
последние строки матрицы А можно выбрать так, чтобы придать любые требуемые
значения компонентам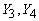
. Это замечание используется в дальнейшем при нахождении вида сопряженных
граничных условий. Поскольку 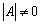
, мы можем обратить преобразование (12) и получить:
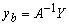 . .
При этом (11) можно переписать как:
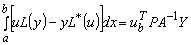
или
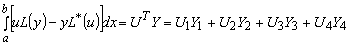 (13), (13),
где 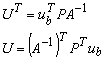 (14) (14)
Билинейная форма 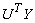 в в
соотношении (13) называется каноническим представлением билинейной формы в
правой части тождества (11).
Для того чтобы найти граничные условия сопряженной задачи, положим в
соотношении (13)
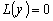 и и 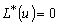 и получим: и получим:
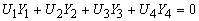 (15) (15)
Из формулы (21) следует, что однородные граничные условия, эквивалентны
равенствам:
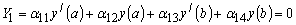 (16) (16)
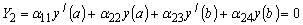 (17) (17)
С учетом равенств (16) и (17) соотношение (15) принимает вид:
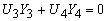 (18) (18)
При ненулевом векторе 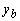
последние две строки матрицы А могут быть выбраны так, чтобы компоненты 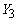
и 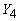 принимали любые принимали любые
требуемые значения, лишь бы 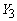
и 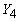 не обращались в не обращались в
нуль одновременно. В частности, нижние строки матрицы А можно выбрать из
условия 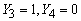 . При этом . При этом
из соотношения (11) следует, что 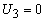
. Аналогичным образом, нижние строки матрицы А можно выбрать так, чтобы
выполнялись равенства 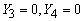
. При этом из соотношения (11) вытекает, что 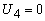
. Таким образом, задача, сопряженная задаче 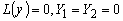
(19)
имеет вид:
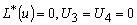 (20) (20)
где 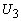 и и 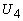
связаны с компонентами 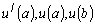
вектора 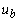
соотношением (14). Краевая задача (19) называется самосопряженной тогда и только
тогда, когда 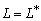 и и
каждая из двух компонент 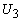
и 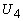 является линейной является линейной
комбинацией 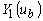 и и 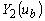
, т.е. 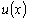
пропорциональна 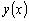 . .
Один из определителей:
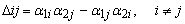
матриц-блоков
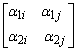
должен быть отличным от нуля. Чтобы иметь возможность сравнить эти результаты с
теми. которые были получены в предыдущем параграфе, предположим. что 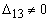
. Далее, выберем такие 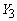
и 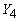 , чтобы строки , чтобы строки
матрицы А были линейно независимы.
Например, положим 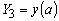 и и 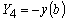 . .
При этом матрица А примет вид:
 (21). (21).
Из формулы (19) следует, что 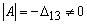 . .
Тогда
 (22) (22)
Подставляя матрицы (20) и (9) в соотношение (14) имеем (14а):
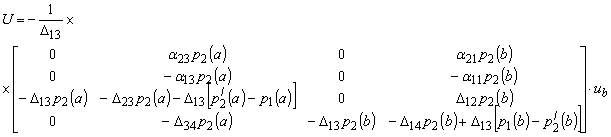
Следовательно, граничные условия сопряженной задачи имеют вид:
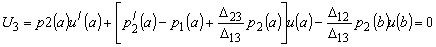
(22)
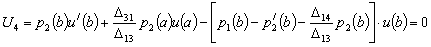
(23)
Для того, чтобы краевые задачи были самосопряженными необходимо, чтобы 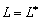
и чтобы каждая из компонент 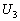
и 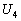 являлась линейной являлась линейной
комбинацией 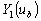 и и 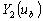
. Как указывалось выше, 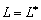
тогда и только тогда, когда 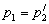
. При этом условия (21) и (20) принимают вид:
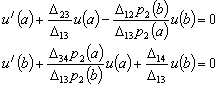 (24) (24)
Разрешая равенства относительно 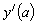 и и 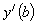 при при 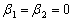 и заменяя и заменяя 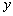 на на 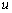 , получаем: , получаем:
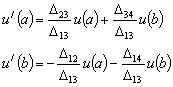 (25) (25)
Сравнивая граничные условия (24) и (25), заключаем, что они совпадают тогда и
только тогда, когда:
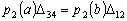 (26) (26)
Краевая задача при 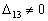
самосопряжена тогда и только тогда, когда выполнены соотношения (24) и равенство 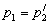
.
Условие разрешимости.
Определив сопряженную краевую задачу, вернемся к решению неоднородной задачи.
Используя определение (25), перепишем формулу Грина в виде:
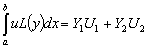 (27) (27)
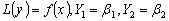 , ,
тогда из соотношения (27) вытекает, что условие разрешимости имеет вид:
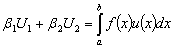 (27) (27)
Для того, чтобы сравнить условие (27) с условием разрешимости, используем связь 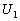
и 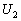 с вектором с вектором 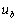
, описываемую формулой (14а) т.е.:
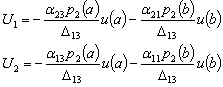 (28) (28)
При этом соотношение (27) принимает вид:
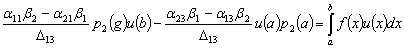
Если иметь дело с граничными условиями общего вида можно выразить какие-либо
два из граничных значений через два других.
| 


