|
|
| Реферат: Приближенное вычисление определенных интегралов |
Реферат: Приближенное вычисление определенных интегралов
Государственный Комитет по рыболовству Российской Федерации
Дальневосточный Государственный Технический
Рыбохозяйственный Университет
Реферат на тему:
«Приближенное вычисление
определенных интегралов.»
Выполнил:
Проверил:
Владивосток
2000
При решении физических и технических задач приходится находить определенные
интегралы от функций, первообразные которых не выражаются через элементарные
функции. Это привело к необходимости вывода приближенных формул вычисления
определенных интегралов. Познакомимся с двумя из них: формулой трапеций и
формулой парабол.
1. Формула трапеций. Пусть требуется вычислить интеграл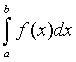 
, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем,
когда f(x)³0. Разобьем отрезок [a, b] на n отрезков точками a=x0
<x1<x2<...<xk-1<xk
<...<xn=b и с помощью прямых х=хk построим n
прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей
трапеций приближенно равна площади криволинейной трапеции, т.е.
Где f(xk-1) и f(xk) - соответственно основания трапеций;
xk - xk-1 = (b-a)/n - их высоты.
Таким образом, получена приближенная формула
которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.
Рассмотрим в качестве примера интеграл 
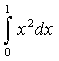. Точное значение этого интеграла находится просто:
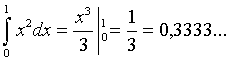Вычислим теперь по формуле трапеций его приближенное значение. Пусть n=5. Тогда
имеем: a=x0=0, x1=0,2, x2=0,4, x3
=0,6, x4=0,8, x5=1=b и соответственно f(x0)=0,
f(x1)=0,04, f(x2)=0,16, f(x3)=0,36, f(x4
)=0,64, f(x5)=1. Следовательно,
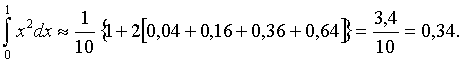Точное значение интеграла равно 0,3333...., поэтому абсолютная ошибка меньше
0,007. Во многих технических задач эта точность достаточна.
Если увеличить число n, то точность будет большей. Так, например, при n=10
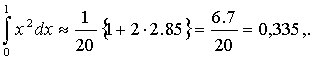т.е. абсолютная ошибка меньше 0,002.
В более полных курсах высшей математики доказывается, что если функция f(x)
имеет на [a, b] непрерывную вторую производную, то абсолютная величина
погрешности формулы трапеций не больше, чем
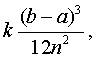где k -наибольшее значение  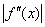на отрезке [a, b].
Следует отметить, что с увеличением n увеличивается не только точность
вычисления определенного интеграла, но и объем вычислительной работы. Однако
здесь на помощь приходят ЭВМ.
Вычислим по формуле трапеции интеграл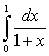 
при n=10. Разобьем отрезок [0, 1] на 10 равных частей точками х0=0, х
1=0,1, ..., х9=0,9, х10=1. Вычислим приближенно
значения функции f(x)=
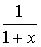в этих точках: f(0)=1,0000, f(0,1)=0.9091, f(0,2)=0,8333, f(0,3)=0.7692,
f(0,4)=0,7143, f(0,5)=0,6667, f(0,6)=0,6250, f(0,7)=0,5882, f(0,8)= 0,5556,
f(0,9)=0,5263, f(1)=0,5000.
По формуле трапеций получаем
Оценим погрешность полученного результата. Так как f(x)=1/(1+x), то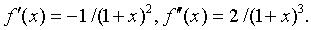 
На отрезке [0, 1] имеем 
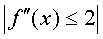. Поэтому погрешность полученного результата не превосходит величины
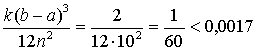Вычислим точное значение данного интеграла по формуле Ньютона-Лейбница:
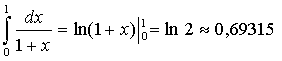Абсолютная ошибка результата, полученного по формуле трапеций, меньше 0,0007.
Это находится в соответствии с данной выше оценкой погрешности.
Идею, которая была использована при построении формулы трапеций, можно
использовать для получения более точных приближенных формул для вычисления
определенного интеграла.
2. Формула парабол. Докажем предварительно две леммы.
Лемма 1.1. Через любые три точки М1 (х1; у
1), М2 (х2; у2), М3 (х
3; у3) с различными абсциссами можно провести единственную
кривую вида
у=Ах2+Вх+С (1)
Доказательство. Подставляя в уравнение параболы (1) координаты точек
М1 , М2 , М3 , получаем систему трех
уравнений первой степени с тремя неизвестными А, В, С:
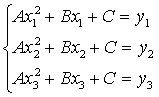Так как числа х1, х2, х3 различны, то определитель этой системы отличен от нуля:
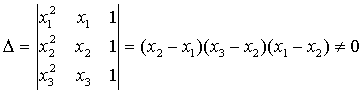Следовательно, данная система имеет единственное решение, т.е. коэффициенты
А, В, С определяются однозначно. g
Отметим, что если А¹0, то кривая (1) является параболой, если А=0, то
прямой.
Лемма 1.2. Площадь s криволинейной трапеции, ограниченной кривой у=Ах
2+Вх+С, проходящей через точки М1 (-h; y1), M2
(0, y2), M3 (h, y3) (рис. 2) выражается
формулой
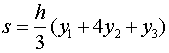 (2)
Доказательство. Подставляя в уравнение у=Ах2+Вх+С
координаты точек М1, М2, М3, получаем у
1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С,
откуда следует, что
2Аh2+2С=у1+у3; С=у2 (3)
Учитывая соотношение (3), имеем
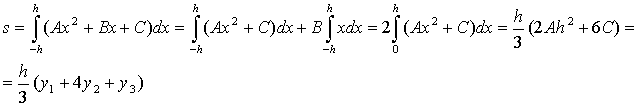Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой
y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0
<x1<x2<...<x2k<x2k+1
<x2k+2<...<x2n-1<x2n=b, а кривую
y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками
М0 , М1 , М2 , ..., М2k
, М2k+1 , М2k+2, ..., М2n-2 , М2n-1
, М2n (рис. 3).
Через каждую тройку точек
М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n
проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим
n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти
трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной
трапеции, соответствующей отрезку [x2k, x2k+2],
приближенно равна площади соответствующей «параболической» трапеции, то по
формуле (2) имеем [в данном случае h=(b-a)/(2n)]
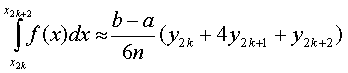где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти
приближенные равенства, получаем приближенную формулу
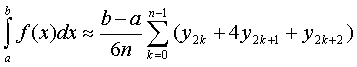или в развернутом виде
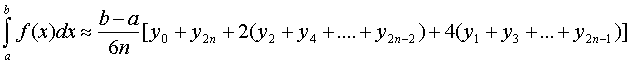Эта формула называется формулой парабол или формулой Симпсона.
В формуле параболы значение функции f(x) в нечетных точках разбиения х1
, х3, ..., х2n-1 имеет коэффициент
4, в четных точках х2, х4, ..., х2n
-2 - коэффициент 2 и в двух граничных точках х0=а, х1
, х2n =b - коэффициент 1.
Геометрический смысл формулы Симпсона очевиден: площадь криволинейной
трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется
суммой площадей фигур, лежащих под параболами (прямыми).
В полных курсах высшей математики доказывается, что если функция f(x) имеет
на [a, b] непрерывную производную четвертого порядка, то абсолютная величина
погрешности формулы Симпсона не больше чем
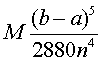где М - наибольшее значение 
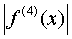на отрезке [a, b]. Выше отмечалось, что погрешность формулы трапеций оценивается
числом
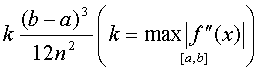Так как n4 растет быстрее, чем n2, то погрешность формулы
Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы
трапеций. Этим и объясняется, что формула Симпсона позволяет получить большую
точность, чем формула трапеций.
Для сравнения точности приближенных формул вычислим еще раз интеграл
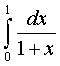 , но теперь по
формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части
точками х0=0, х1=1/4, х2=1/2, х3
=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в
этих точках у0=1,0000, у1=0,8000, у2=0,6667, у
3=0,5714, у4=0,5000.
По формуле Симпсона получаем
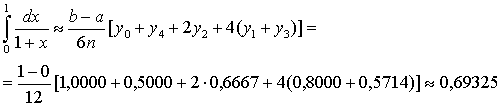Оценим погрешность полученного результата. Для подынтегральной функции
f(x)=1/(1+x) имеем: f(4)(x)=24/(1+x)5 , откуда следует,
что на отрезке [0, 1]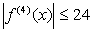 
. Следовательно, можно взять М=24, и погрешность результата не превосходит
величины 24/(2880× 44),0б0004. Сравнивая приближенное значение
с точным, заключаем, что абсолютная ошибка результата, полученного по формуле
Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой
погрешности и, кроме того, свидетельствует, что формула Симпсона значительно
точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления
определенных интегралов используют чаще, чем формулу трапеций.
Как отмечалось выше, приближенные формулы для вычисления определенного
интеграла применяют в тех случаях, когда первообразная подынтегральной
функции не выражается через элементарные функции.
Вычислим, например, интеграл 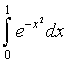 по формуле Симпсона с точностью до 0,001.
Чтобы выбрать необходимое для получения заданной точности число 2n, найдем f
(4)(x). Последовательно дифференцируя функцию f(x)=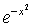
, получаем
f(4)(x)=4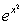 (4х4-12х2+3)
Так как на отрезке [0, 1]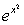 
£1, ½4х4-12х2+3½£5, то 
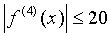. Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем
20/2880n4<1/1000, откуда n4 >1000/144. Для того
чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.
Разобьем теперь отрезок [0, 1] на четыре равные части точками х0=0, х
1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим
приближенно значения функции f(x)=
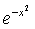в этих точках у0=1,0000, у1=0,9394, у2=0,7788,
у3=0,5698, у4=0,3679. Применяя формулу Симпсона,
получаем
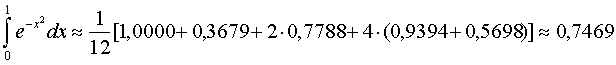Таким образом,  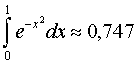с
точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и
заменив рассматриваемый интеграл суммой, стоящей в правой части формулы
Симпсона, мы вычислили данный интеграл с необходимой точностью.
В заключении отметим, что каждый из изложенных методов приближенного
вычисления интегралов содержит четкий алгоритм их нахождения, что позволяет
широко применять эти методы для вычислений на ЭВМ. Таким образом, указанные
методы - эффективное средство вычисления интегралов. Для интегралов, которые
нельзя выразить через элементарные функции, с помощью ЭВМ и простейших
приближенных методов можно составить таблицы их значений.
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|
