Шпора: Матанализ

1Натуральные числа – 1,2,3,4, .., счёт предметов, указание порядкового номера.

Натуральные числа также называют положительными целыми числами. Числа –1,-2,

-3, ., противоположные натуральным называются отрицательными целыми числами.

Число 0 тоже целое. Рациональные числа – целые и дроби (+,-) Вид М/N, где (N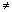

0) M и N- взаимно простые целые числа. Иррациональные - √2 все

вышепереч-е + бесконечные непериодич. дроби. Все эти числа – действительные.

Компл. число Z1=A1+iB1; i²=-1

2 Z1±Z2=(A1±A2)+i(B1±B2)

Z1*Z2=(A1+iB1)*(A2+iB2)

Z1/Z2=(a1+ib1)(a2-ib2)/(a2+ib2)(a2-ib2)=(a1a2+b1b2)+

i(b1a2-a1b2)\a2²+b2²=(a1a2+b1b2/a2²+b2²)+i* (b1a2-

a1b2/a2²+b2²)

3 Тигонометрическая форма комплексного числа

Z=a+ib=r*cosφ+i*r*sinφ=r*(cosφ+i*sinφ)

r – модуль; φ – аргумент. b – y; a – x.

4 Zª=rª(cos Aφ+i*sin Aφ)

5 ª√Z=ª√r(cos φ+2πk/а +i *sin φ+2πk/a)

k∈(1;2;3.a-1)

Все корни А-ой степени лежат на окружности r=| Z |¹\а и являются

вершинами правильного А-угольника, вписанного в эту окружность.

6 Переменная вел. Х, принимающая последовательно ( с возрастанием номера n )

значения х1,х2,х3..хN называется числовой последовательностью

1,1,1,1,1.1

1,1/2,1/3.1/N

1,-1,1,-1.(-1)ª

Xn,n∈N

Число А наз. пределом последовательности Хn если для любого сколь угодно малого

положит. числа E>0 найдётся такой номер N(E), что как только n>N(E) то

имеет место неравенство | Xn – A | < E

lim Xn = A

n→∞

Число А есть предел последовательности Xn если для любого ε > 0 найдётся

такой номер N, начиная с которого (при n>N) все члены последовательности

будут заключены в ε-окрестности какой бы она узкой ни была. Вне этой

окрестности может быть лишь конечное число членов этой последовательности.

7 Если последовательность Хn монотонна и ограничена, то она имеет предел

(сходится).

Cвойства пределов:

если Хn=С то lim Xn=C

n→∞

пусть lim Xn=A, a lim Yn=B тогда lim (Xn±Yn)=A±B

n→∞ n→∞ lim (Xn*Yn)=A*B

lim (Xn/Yn)=A/B ; B≠0

если Xn≤Yn для n∈N то lim Xn ≤ lim Yn

n→∞ n→∞

8 Eсли Хn сходится (имеет предел) то Хn ограничена

Последовательность Xn; n∈N наз. ограниченной если существует

положительное число М, что выполняется нер-во | Xn |≤M; n∈N

Если lim Xn=0, то Xn; n∈N наз. БМВ обознач (αn,βn,γn)

n→∞

Св-ва БМВ:

lim αn=0

n→∞

lim (αn±βn)=0

n→∞

lim (Xn*αn)=0; если Xn-ограничена

n→∞

В произведении БМВ можно заменять на эквивалентную БМ. В алгебраической сумме

замену можно производить в том случае если не происходит сокращения БМ одного

порядка с Х:

sin X ~ X eª-1 ~ a

tg X ~ X (1+x)ª ~ ax

1 – cos X ~ X²/2 arctg X ~ X

LOGe(1+X) ~ X xª-1 ~ aLNx

9 Сумма эл-тов числовой последовательности наз. числовым рядом.

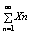
Сумма n членов ряда – n частичная сумма ряда

Если при n→∞ lim Sn=S, то ряд сходящийся, S сумма ряда .

Ряд наз. сходящимся если сущ. конечный предел последовательности его

частичных сумм.

Прим:

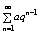при каких q сходится и расходится ?

сходится к сумме S=a/1-q при | q |<1 и расход-ся при | q |≥1

10 Признак сравнения двух знакоположит-х рядов.

есть 2 знакполож. ряда ∑Ak,∑Bk так что 0≤Ak≤Bk k∈N

тогда если ∑Bk⇒ то ∑Ak тоже ⇒ и наооборот если

меньший ряд не сходится то и больший тоже.

11 Признак Даламбера

∑Un c положительными членами сущ. lim Un+1/Un =l

n→∞

то ряд сходится если l<1 и расходится если l>1, если l=1 то вопрос о

сходимости нерешён.

Признак Коши

∑An – знакополож. ряд lim ª√An=q

n→∞

q<1 – сходится ; q>1 – расходится.

12 Знакопеременный ряд а1-а2+а3-а4.+ (-1)в степ.(n-1)*An

An>0

Признак Лейбница:

Если члены ряда (знакопер) убывают а1>a2>a3>.An и

предел Аn при n→∞ =0 то ряд сходится

пример 1-1/2+1/3-1/4.+(-1)(n-1)*1/n

13 Имеет место функциональная зависимость между двумя переменными величинами

х и у если задан закон y=f(x), согласно которому каждому х∈Х

соответствует значение y∈Y. х-аргумент

y=kx+b – линейная ф-ия

y=ax²+bx+c – квадратичная ф-ия

Обратная ф-ия – ф-ия x=φ(y) наз. обратной ф-ией к прямой ф-ии y=f(x)

если x=φ(f(x)) для всех х∈Х

Графики взаимно обратных ф-ий симметричны относительно прямой у=х.

y=Xª и y=LOGxA – примеры

14 Число B называется пределом ф-ии в f(x) при x, стремящемуся к x0 (или в точке

x0) если для любого, сколь угодно малого положительного числа ε>0,

найдётся такое положительное число δ(ε)>0 что для всех х не равных

х0 и удовлетворяющих условию | x-x0 |<δ выполняется нерав-во | f(x)-B

| < ε

lim f(x)=B

x→x0

Смысл состоит в том, что для всех значений х, достаточно близких к х0,

значения ф-ии f(x) как угодно мало отличаются от числа В (по модулю)

15 lim f(x)=B

x→x0

Если B=f(x0), то ф-ия f(x) – непрерывна в точке х0.

св-ва :

lim c=c

x→x0

если f(x)=b, φ(x)=c то lim (f(x)±φ(x))=b±c

x→x0

lim (f(x)*φ(x))=b*c

x→x0

lim (f(x)/φ(x))=b/c (c≠0)

x→x0

Если f(x)≤φ(x)≤g(x) и lim f(x)=lim g(x) =b то lim φ(x)=b

x→x0 x→x0 x→x0

если при этом b=f(x0); c=φ(x0) то св-во 2 можно записать:

(Если f(x) или φ(х) непрерывны в т. х0 то в т.х0

непрерывны сумма, разность, произведение и

частное(φ(х0))≠0 этих функций

Если ф-ия непрерывна в каждой точке отрезка, то она непрерывна на этом отрезке

16 Линейная ф-ия непрерывна в любой точке А∈(-∞;+∞)

y=kx+b=f(x)

f(A)=kA+b

k≠0 ⇒ | f(x)-f(a) |<ε | kx-b-ka+b | <ε

| k (x-f) | <ε

| k |*| x-a | <ε

| x-a | < ε/| k |=δ(ε)

y=ax²+bx+c (-∞;+∞)

17 y=Bª (B>0)

Докажем, что y=Bª непрерывна на (-∞;+∞)

lim Bª=1

a→0

| Bª-1 | <ε 1) B=1

2) B>1

-ε < Bª-1 < ε 1-ε < Bª < ε+1

LOGb(1-ε)<a<LOGb(1+ε)

min {-LOGa(1-ε); LOGa(1+ε)}= δε

| x | < δε

LOGaB

18 y=cos x (-∞; +∞)

| cos x – cos a | < ε

| 2 sin (x-a)/2 + sin (x+a)/2 | < ε

2 | sin (x-a)/2 | + | sin (x+a)/2 | < ε

2 | sin (x-a)/2 | < ε

| x-a | < ε =δ(ε)

y=sin x (-∞; +∞)

y=tg x=sin x/cos x кроме x=π/2+πk

y=ctg x=cos x/sin x кроме x=πk

19 Первым замечательным пределом называется

lim sin x/x=1

x→x0

20 Второй замечательный предел

lim(1+1/a)ª=e

a→∞

Число е (число Эйлера, неперово число) играет важную роль в матанализе.

lim (1+a)¹’ª=e

a→0

21 Пусть имеется ф-ия y=f(x), определённая на (а; в), говорят что ф-ия имеет

в т. х0∈(а; в) производную f ’(x0) если существует предел

lim (f(x)-f(x0))/(x-x0)

x→x0

Производной ф-ии y=f(x) в точке х0 называется предел отношения приращения ф-

ии к приращению аргумента, когда приращение аргумента стремится к нулю.

Ф-ия имеющая производную в каждой точке интервала называется дифференцируемой

на этом интервале.

Геометрический смысл производной: пр-ая f `(x0) есть угловой коэфф. (tg угла

наклона) касательной, проведённой к кривой y=f(x) в точке х0 , k=f ‘(x0)

у=f ‘(x0)(x - x0)

Механический смысл производной: пр-ая пути по времени s ‘(t0) есть

скорость точки в момент t0: V(t0)=s ‘(t0)

Определение для любой точки

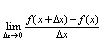
22 Производная алгебраической суммы конечного числа дифференцируемых ф-ий

равна такой же сумме производных этих ф-ий

(u±v)`=u`± v`

Производная произведения двух дифференцируемых ф-ий равна произведению пр-ой

первого сомножителя на второй плюс произведение первого сомножителя на про-ую

второго:

(uv)`=u`v + uv`

Постоянный множитель можно выносить за знак

производной

(cu)`=cu`

Производная произведения нескольких

дифференцируемых ф-ий равна сумме произведений

производной каждого из сомножителей на все остальные

(uvw)`=u`vw+uv`w+uvw`

23 Производная частного двух ф-ий u(x)/v(x), если v(x)≠0

равна дроби, числитель которой есть разность произведений знаменателя дроби

на производную числителя и числителя дроби на производную знаменателя есть

квадрат прежнего знаменателя: (u/v)`=(u`v-uv`)/v²; v≠0

(u/c)`=1/c*u`

(c/u)`=-cv`/v² c=const

24 (xª)`=axªˉ¹

25 (LNx)`=1/x

(eª)`=eª

Для дифференцируемой ф-ии с производной, не равной

0, производная обратной ф-ии равна обратной величине

производной данной ф-ии

X`y = 1/Y`x

26 (sin x)`=cos x

(cos x)`=-sin x

(tg x)`=1/cos²x

(ctg x)`=-1/sin²x

27 Если y=f(u) и u=φ(x) – дифференцируемые ф-ии от своих аргументов, то

производная сложной ф-ии существует и равна производной данной ф-ии по

промежуточному аргументу и умноженной на производную самого промежуточного

аргумента по незавмсимой переменной х

y`=f`(u)*u`

y=f(u(x)) Fx`=Fu`*Ux`

Пример:

y=(√x+5)³ y`=?

y=u³, где u=√x+5

по формуле :

y`=3u`*u`=3(√x+5)²(√x+5)`=3(√x+5)²/2√x

28 Дифференциалом ф-ии наз. линейная часть приращения ф-ии (относительно

Δх), равная произведению производной на приращение независимой

переменной.

dy=f`(x)Δx

Дифференциал независимой переменной равен приращению этой переменной.

Геометрический смысл: Дифференциал ф-ии есть приращение ординаты касательной,

проведённой к графику ф-ии y=f(x) в данной точке когда х получает приращение

Δх

29 При исследовании ф-ий используется следующий алгоритм:

1 ООФ, ОЗФ

2 Непрерывность ф-ии

3 Нахождение асимптот

4 Экстремумы и интервалы монотонности

5 Интервалы выпуклости и т. перегиба

6 Чётность нечётность, периодичность

7 Т. пересечения с Ох и Оу

(3)Если для некоторого х0 имеет место предел f(x)=∞ при

х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой

f(x)

Если предел f(x)=b при x→∞ то говорят, что у=b явл.

горизонтальной асимптотой f(x)

Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел

(f(x)-kx)=b, то y=kx+b является наклонной асимпт-й

(4)Если производная ф-ии положительна (отрицательна)

внутри некоторого промежутка Х то ф-ия возрастает

(убывает) на этом промежутке

Если при переходе через т. х0 производная

дифференцируемой ф-ии меняет свой знак и в т. х0

равна 0 то х0-точка экстремума (минимума или

максимума)

(5)Точкой перегиба непрерывной ф-ии (f``(x)=0) наз. т. в

разделяющая интервалы, в которых ф-ия выпукла вниз и

вверх.

Ф-ия y=f(x) называется выпуклой внизу на интервале

(a;b) если f``(x)>0 на (a;b); ф-ия называется выпуклой

вверх на (a;b) если f``(x)<0 на (a;b)

30 Асимптотой графика ф-ии y=f(x) называется прямая, обладающая тем

свойством, что расстояние от точки (х, f(x)) до этой прямой

стремится к 0 при неограниченном удалении точки графика от начала координат.

Если для некоторого х0 имеет место предел f(x)=∞ при

х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой

f(x). Вертикальные асимптоты следует искать в точках

разрыва ф-ии или на концах её ООФ (а; в) если аи в –

Страницы: 1, 2