Шпора: Шпора по матану
1.Мн-во операций над мн-вами
Мн-во – совокупность объектов, обладающих определенным св-вом.
Пересечением двух мн-в А и В н-ся мн-во С, состоящее из Эл-ов, принадлежащих
как мн-ву А, так и мн-ву В.(А={1,2,3}, B={2,5}, AΩB={2}) Объединением
двух мн-в А и В н-ся мн-во С, состоящее из Эл-ов, принадлежащих хотя бы
одному из мн-в А или В.(A={1,2,3}, B={2,5} AuB={1,2,3,5}Разностью С двух мн-в
А и В н-ся мн-во, состоящ. Из Эл-ов мн-ва А и не принадл. В(Разностью мн-ва
целых чисел и мн-ва четных чисел явл. Мн-во нечетных чисел) Если А подмн-во
В, то разность В\А н-ся дополнением А до В. Дополнением мн-ва А н-ся мн-во,
состоящ. Из Эл-ов универсального мн-ва не принадлежащих мн-ву А.
2.Мн-во вещ.чисел, основные св-ва точных граней
Наиболее употребительные числовые мн-ва: N-мн-во натуральных чисел Q-мн-во
рациональных чисел R-мн-во вещественных чисел C-мн-во комплексных чисел
(Cегмент: [a,b]=a<x≤b Полунтервал: (a,b]=x
[a,b)=x [a,+∞)=a≤x<∞
(-∞,a]=xИнтервал: (a,b)=a<x<b
(a,+∞)=a<x<+∞ (-∞,a)=x
R=x=(-∞,+∞) ). Все эти мн-ва н-ся
промежутками a,b –концами промежутков. [a,b],(a,b),[a,b),(a,b] – конечные
промежутки, остальные-бесконечные!
+можно взять из 3 вопроса
3.Грани числовых мн-в, св-во граней
Пусть Х – непустое мн-во веществ. чисел. Мн-во Х назся огран.
сверху(снизу), если сущ-ет число с такое, что для любого х Х вып-ся
неравенство с³х(х³с). Число с наз-ся верхн.(нижн.) гранью мн-ва Х.
Мн-во, огран. сверху и снизу наз-ся ограниченым Если мн-во имеет 1
верхнюю грань то она имеет их бесчисленное мн-во.
Пример X=R+ - ограничено снизу, но не сверху, значит не ограничено.
Точные грани числовых мн-в Пусть мн-во Х ограничено сверху, если
это мн-во содержит макс число, т.е. наименьшую из своих верхних граней, то это
число назся макс мн-ва Х и обозначается Х*=maxX. Если мн-во содержит мин число
Х* , то оно min мн-ва Х Пример Х=[0,1) то max[0,1) не $.
min [0,1)=0 Число Х* наз-ся точной верхн. гранью, мн-ва Х, если
во-первых оно явл. верхн. гранью этого мн-ва, а во-вторых при сколь угодном
уменьшении Х* получ. число перестает быть верх. гранью мн-ва. Верхн.
грань – supX=x*, а нижн. грань infX=x* Теорема. Любое
непустое ограниченное сверху (снизу) числ. мн-во имеет точную верх(ниж) грань.
Таким образом у огран. мн-ва обе грани $, док-во основано на непрерывности мн-ва
действит. Чисел.
4.Th о сущ. т.в.г. и т.н.г.
Теорема. Любое непустое ограниченное сверху (снизу) числ. мн-во имеет точную
верх(ниж) грань.
Док-во: Пусть Х непустное мн-во, ограниченное сверху. Тогда Y- мн-во чисел,
ограничивающих мн-во Х сверху, не пусто. Из определения верхней грани
следует, что для любого х€Х и y€Y любого выполняется нер-во х≤у. В силу
св-ва непрерывности вещ.чисел существует такое с, что для любых х и у
выполняется нер-во х≤с≤у. Из первого нер-ва следует, что число с
ограничивает мн-во Х сверху, т.е. является верхней гранью. Из второго нер-ва
следует, что число ч явл.наименьшим из таких чисел,т.е. явл точной
верхн.гранью. Теорема док-на. Аналогична теорема о т.н.г
5.Числовые последовательности, действия над ними
Если для каждого нат. числа n определено некоторое правило сопоставляющее ему
число xn, то мн-во чисел х1,х2, . ,хn, .(1,2,3,n –внизу) наз-ся числовой
последовательностью и обозначается {xn}, причем числа образующие данную посл-
ть наз-ся ее эл-ми, а эл-т хn общим эл-том посл-ти . Над числовыми
последовательностями можно выполнять след. Арифметические операции:
произведение, сумма, разность, произведением на число, частное.
6.Огранич и неогранич пос-ти
Посл-ть {xn} наз-ся огран. сверху(снизу), если найдется какое-нибудь число {xn}
M(m) xn£M "n (xn³m "n) посл-ть наз-ся огранич., если она огранич.
сверху и снизу.
Посл-ть {xn} наз-ся неогранич., если для любого полного числа А сущ-ет эл-т хn
этой посл-ти, удовлетворяющий неравенству ½xn½>А.
7. Б-м и б-б пос-ти: опр, осн. Св-ва, связь между ними
Пос-ть Xn н-ся б-б, если для любого положительного числа А существует номер N
такой, что при всех n>N выполняется нер-во |Xn|>A, т.е.
("A>0)($N=N(A))("n>N):|Xn|>A Любая б-б пос-ть явл. неограниченной.
Однако неограниченная пос-ть может и не быть б-б.
Пос-ть {An} н-ся б-м, если для любого положительного числа ε (сколь бы
малым мы его ни взяли) существует номер N=N(ε) такой, что при всех n>N
выполняется нер-во |An|< ε, т.е. ("ε>0)($N=N(ε))(
"n>N):|An|< ε
Св-ва: 1.Если {Xn} б-б пос-ть и все ее члены отличны от нуля, то по-сть
{1\Xn} б-м и обратно. 2.Сумма и разность двух б-м пос-тей есть б-м пос-ть.
(следствие: алгебраическая сумма любого конечного числа б-м постей есть б-м
пость.) 3.Произведение двух б-м постей есть б-м пость.4. Произведение
ограниченной пости на бесконечно малую пость есть пость б-м.
8.Понятие сходящихся постей, lim пости.
Опр Если для любого e >0 найдется такой номер N, для любого n
>N:½xn-a½< e
Все посл-ти имеющие предел наз-ся сходящимися, а не имеющее его наз-ся
расходящимися.
Опр Число а н-ся пределом пости Xn для любой точки окрестности а, сущ. N=N(e),
такой, что все Эл-ты Xn с номерами n>N находятся в этой e-окрестности.
9.Основные св-ва сход. Постей
Теорема «Об единственности пределов»
Если посл-ть xn сходится, то она имеет единственный предел. Док-во (от
противного)
{xn} имеет два разл. Предела a и b, а¹b. Тогда согласно определению
пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за
исключением конечного числа и аналогичным св-вом обладает любая окрестность в
точке b. Возьмем два радиуса e= (b-a)/2, т.к. эти окрестности не
пересекаются, то одновременно они не могут содержать все эл-ты начиная с
некоторого номера. Получим противоречие теор. док-на.
Теорема «Сходящаяся посл-ть ограничена»
Пусть посл-ть {xn}®а e >о N:"n>N½xn-a½<e эквивалентна
а-e<xn<a+e "n>N => что каждый из членов посл-ти удовлетворяет
неравенству½xn½£ c = max
{½a-e½,½a+e½,½xn½,.,½xn-1½}
Теорема «Об арифметических дейсьвиях»
Пусть посл-ть {xn}®a,{yn}®b тогда арифметические операции с этими посл-тями
приводят к посл-тям также имеющие пределы, причем:
а) предел lim(n®¥)(xn±yn)=a±b
б) предел lim(n®¥)(xn*yn)=a*b
в) предел lim(n®¥)(xn/yn)=a/b, b¹0
Док-во: а)xn±yn=(а+an)±(b+bn)=(a±b)+(an±bn) Правая часть полученная в
разности представляет сумму числа a+b б/м посл-тью, поэтому стоящая в левой
части xn+yn имеет предел равный a±b. Аналогично др. св-ва.
б) xn*yn=(а+an)*(b+bn)=ab+anb+abn+anbn
an*b – это произведение const на б/м
а*bn®0, anbn®0, как произведение б/м.
=> поэтому в правой части стоит сумма числа а*b+ б/м посл-ть. По т-ме О связи
сходящихся посл-тей в б/м посл-ти в правой части xn*yn сводится к a*b
10. Предельный переход в нер-вах.
11. Монотонные пос-ти
Посл-ть {xn} наз-ся возр., если x1<.<xn<xn+1<.;
неубывающей, если x1£x2£.£xn£xn+1£.; убывающей,
если x1>x2>.>xn>xn+1>.; невозр., если
x1³x2³.³xn³xn+1³.
Все такие посл-ти наз-ся монотонными. Возр. и убыв. наз-ся строго монотонными
Монотонные посл-ти ограничены с одной стороны, по крайней мере. Неубывающие
ограничены снизу, например 1 членом, а не возрастыющие ограничены сверху.
12. Число е
Рассмотрим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1) .
Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но
явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается
символом е»2,7128.
Док-ем формулу lim(n->∞)(1+1/n)^n(в степени n)=е
yN=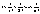 ; zN=yN + ; zN=yN +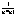
1) yN монотонно растет
2) yN<zN
3) zN-yN®0
4) zN монотонно убывает
Доказателство:
zN-zN+1 = yN +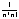 - yN+1 - - yN+1 -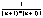 = = 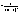 + +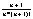 - -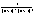 = =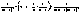
2=y1<yN<zN<z1=3
e = Lim yN = Lim zN - по лемме о вложенных
промежутках имеем: yN<e<zN = yN +
1/(n*n!)
Если через qN обозначить отношение разности e - yN
к числу 1/(n*n!), то можно записать e - yN = qN
/(n*n!), заменяя yN его развернутым выражением получаем e = y
N + qN/(n*n!), qÎ(0,1)
Число e иррационально:
Доказательство(от противного): Пусть e=m/n, mÎZ, nÎN
m/n = e = yN + qN/(n*n!)
m*(n-1)!= yN*n! + qN/n, где (m*(n-1)! & yN*n!)ÎZ, (qN/n)ÏZ => противоречие
13. Th о вложенных промежутках
Пусть на числовой прямой задана посл-ть отрезков [a1,b1],[a2,b2],.,[an,bn],.
Причем эти отрезки удовл-ют сл. усл.:
1) каждый посл-щий вложен в предыдущий, т.е. [an+1,bn+1]Ì[an,bn],
"n=1,2,.;
2) Длины отрезков ®0 с ростом n, т.е. lim(n®¥)(bn-an)=0. Посл-ть с
указанными св-вами наз-ют вложенными.
Теорема Любая посл-ть вложенных отрезков содержит единную т-ку с
принадлежащую всем отрезкам посл-ти одновременно, с общая точка всех отрезков
к которой они стягиваются.
14.Понятие ф-ии, способы задания, классификация
15.Предел ф-ии в точке(Гейне,Коши,правый,левый) Предел ф-ии на бесконечности
16. Th о пределе ф-ии
17. Первый замечательный предел
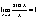
Доказательство: докажем для 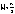 справедливость неравенства справедливость неравенства 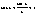
В силу четности входящих в неравенство ф-ий, докажем это неравенство на
промежутке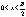
Из рисунка видно, что площадь кругового сектора
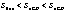
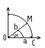 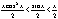 , так как х>0, то , так как х>0, то 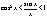 , ,
2. следовательно, что 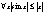
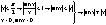
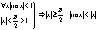
1. Покажем, что 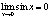
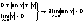
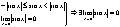
2. Докажем, что 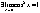
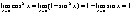
3. Последнее утверждение:
Страницы: 1, 2, 3
| 


