|
|
| Доклад: Основная Теорема Алгебры |
Доклад: Основная Теорема Алгебры
Основная теорема алгебры.
Всякий многочлен с любыми комплексными коэффициентами , степень которого не
меньше единицы имеет хотя бы один корень, в общем случае комплексный.
План доказательства.
Лемма №1. Многочлен f(x) является непрерывной функцией
комплексного переменного x.
Лемма №2. Если данн многочлен n-ой степени, n>0,
f(x)=a0xn+a1xn-1+.+an
с произвольными комплексными коэффициентами и если k- любое
положительное действительное число, то для достаточно больших по модулю
значений
|anxn|>k|axn-1+anxn-2+..+a0|
Лемма №3.
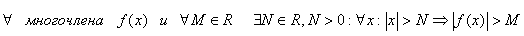 Лемма №4.(Лемма Даламбера).
Лемма №4.(Лемма Даламбера).
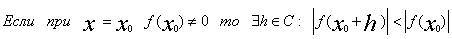 Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в
замкнутом круге Е, то она ограничена.
Лемма №6.
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в
замкнутом круге Е, то она ограничена.
Лемма №6.
Действительная функция комплексного переменного f(x) непрерывная в
замкнутом круге Е достигает своего минимума и максимума.
Доказательство основной теоремы.
Лемма №1.
Надо доказать, что 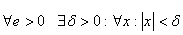 |f(x0+x)-f(x0)|<e.
Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0
Если A=max(|a0 |,|a1|,.,|a n-1|) и |f(x0+x)-f(x0)|<e.
Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0
Если A=max(|a0 |,|a1|,.,|a n-1|) и 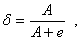 (1)
то |f(x)|=|a0xn+.+an-1x| (1)
то |f(x)|=|a0xn+.+an-1x| 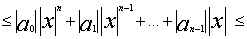
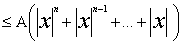 ,
т.к |x|<б ,и из (1) б<1, то
т.к. a0=0 то f(0)=0 ,
т.к |x|<б ,и из (1) б<1, то
т.к. a0=0 то f(0)=0 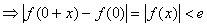 Что и требовалось доказать.
Теперь докажем непрерывность любого многочлена.
f(x0+x)=a0(x0+x)n+.+an
pаскрывая все скобки по формуле бинома и собирая вместе члены с
одинаковыми степенями x получим
Что и требовалось доказать.
Теперь докажем непрерывность любого многочлена.
f(x0+x)=a0(x0+x)n+.+an
pаскрывая все скобки по формуле бинома и собирая вместе члены с
одинаковыми степенями x получим
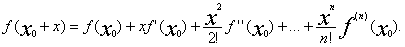
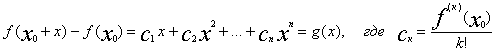 Многочлен g(x)-это многочлен от x при x0 =0 и а0=0
Многочлен g(x)-это многочлен от x при x0 =0 и а0=0 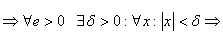 |f(x0+x)-f(x)|=|g(x)|<e
Лемма доказана.
Лемма №2
Если дан многочлен n-ой степени, n>0,
f(x)=a0xn+a1xn-1+.+an
с произвольными комплексными коэффициентами и если k- любое
положительное действительное число, то для достаточно больших по модулю
значений x верно неравенство:
|a0xn|>k|a1xn-1+a2xn-2+..+an| (2)
Доказательсво.
Пусть А=max( |f(x0+x)-f(x)|=|g(x)|<e
Лемма доказана.
Лемма №2
Если дан многочлен n-ой степени, n>0,
f(x)=a0xn+a1xn-1+.+an
с произвольными комплексными коэффициентами и если k- любое
положительное действительное число, то для достаточно больших по модулю
значений x верно неравенство:
|a0xn|>k|a1xn-1+a2xn-2+..+an| (2)
Доказательсво.
Пусть А=max(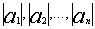 ), тогда ), тогда
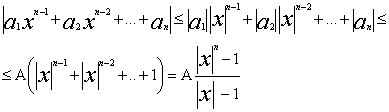 пологая |x|>1, получим
пологая |x|>1, получим
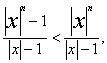 откуда
откуда
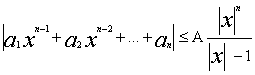 следовательно неравенство (2) будет выполняться если |x|>1 и
следовательно неравенство (2) будет выполняться если |x|>1 и
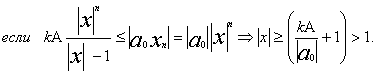 Лемма №2 доказана.
Лемма №3.
Лемма №2 доказана.
Лемма №3.
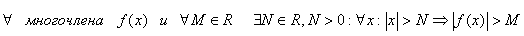 Доказательство.
Доказательство.
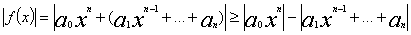 (3)
применим лемму 2: при k=2 существует такое N1 , что при |x|> N1
|a0xn|>2|a1xn-1+a2xn-2+..+an|
откуда
|a1xn-1+a2xn-2+..+an|<|a0xn|/2
тогда из (3)
(3)
применим лемму 2: при k=2 существует такое N1 , что при |x|> N1
|a0xn|>2|a1xn-1+a2xn-2+..+an|
откуда
|a1xn-1+a2xn-2+..+an|<|a0xn|/2
тогда из (3)
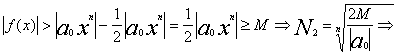 при |x|>N=max(N1 ,N2) |f(x)|>M что и тебовалось доказать.
Лемма №3(Лемма Даламбера).
Если при x=x0 многочлен f(x) степени n,
при |x|>N=max(N1 ,N2) |f(x)|>M что и тебовалось доказать.
Лемма №3(Лемма Даламбера).
Если при x=x0 многочлен f(x) степени n,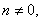 не обращаеться в нуль, то существует такое приращение h, в общем случае
комплексное, что
|f(x0+h)|<|f(x)|
Доказательство.
не обращаеться в нуль, то существует такое приращение h, в общем случае
комплексное, что
|f(x0+h)|<|f(x)|
Доказательство.
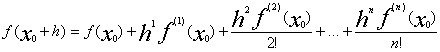 По условию f(x0) не равно нулю, случайно может быть так, что x0
является корнем f’(x),..,f(k-1) (x). Пусть k-я производная будет
первой, не имеющей x0 своим корнем. Такое k существует т.к.
f(n)( x0)=n!a0
Таким образом
Т.к f(x0) не равно нулю то поделим обе части уравнения на f(x0)
и обозначим
По условию f(x0) не равно нулю, случайно может быть так, что x0
является корнем f’(x),..,f(k-1) (x). Пусть k-я производная будет
первой, не имеющей x0 своим корнем. Такое k существует т.к.
f(n)( x0)=n!a0
Таким образом
Т.к f(x0) не равно нулю то поделим обе части уравнения на f(x0)
и обозначим 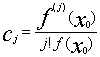
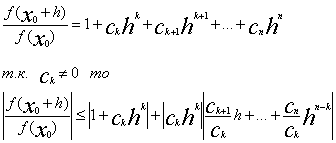 Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его
аргумент.
По лемме№1:
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его
аргумент.
По лемме№1: 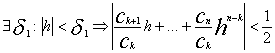 С другой стороны при
С другой стороны при
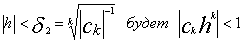 (4)
Пусть |h|<min(б1, б2), тогда (4)
Пусть |h|<min(б1, б2), тогда
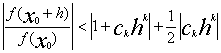 Теперь выберем аргумент h так, чтобы ckhk было
действительным отрицательным числом.
Теперь выберем аргумент h так, чтобы ckhk было
действительным отрицательным числом.
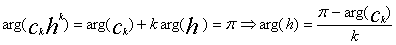 При таком выборе ckhk=-| ckhk| следовательно учитывая (4) получим
При таком выборе ckhk=-| ckhk| следовательно учитывая (4) получим

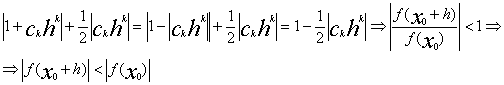 Что доказывает лемму Даламбера.
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в
замкнутом круге Е, то она ограничена.
Доказательство.
Что доказывает лемму Даламбера.
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в
замкнутом круге Е, то она ограничена.
Доказательство.
Предположим, что это не верно тогда
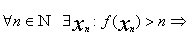 получена бесконечная ограниченная последовательность xn,
из нее можно выбрать сходящуюся подпоследовательность
получена бесконечная ограниченная последовательность xn,
из нее можно выбрать сходящуюся подпоследовательность 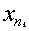 , пусть ее предел равен x0. Так как круг Е замкнут, то x
0 пренадлежит Е. Тогда так как f(x) непрерывна
, пусть ее предел равен x0. Так как круг Е замкнут, то x
0 пренадлежит Е. Тогда так как f(x) непрерывна
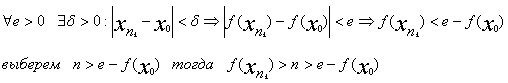 получено противоречие, следовательно неверно, предположение о неограничености
f(x).
Лемма №6.
Действительная функция комплексного переменного f(x) непрерывная в
замкнутом круге Е достигает своего минимума и
максимума.
Доказательство.
Докажем это утверждение для максимума.
Так как f(x) непрерывна в Е, то она ограничена и следовательно
существует M=sup{ f(x)}. Рассмотрим функцию
получено противоречие, следовательно неверно, предположение о неограничености
f(x).
Лемма №6.
Действительная функция комплексного переменного f(x) непрерывная в
замкнутом круге Е достигает своего минимума и
максимума.
Доказательство.
Докажем это утверждение для максимума.
Так как f(x) непрерывна в Е, то она ограничена и следовательно
существует M=sup{ f(x)}. Рассмотрим функцию 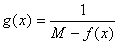 .
Если f(x) не достигает своего максимума, то M> f(x)
следовательно M-f(x)>0 , следовательно g(x) непрерывна в Е.
.
Если f(x) не достигает своего максимума, то M> f(x)
следовательно M-f(x)>0 , следовательно g(x) непрерывна в Е.
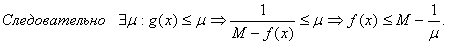 Полученое противоречит тому, что M=sup{ f(x)}. Следовательно
функция достигает свего максимума. Аналогично доказывается достижение минимума.
Доказательство основной теоремы.
Пусть дан многочлен f(x), очевидно что если an-свободный член, то
f(0)= an. Теперь применим лемму№3: возьмем М=|f(0)| =|an|
тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Е
ограниченный окружностью с центром в нуле и радиусом N, включая границы круга.
Так как (по лемме №1) многочлен f(x)-непрерывен, то и |f(x)|-непрерывен внутри
замкнутого круга Е, следовательно(по лемме №6), существует такая точка x0
, что для всех x из E выполняется неравенство |f(x)|>=|f(x0)|. x
0 является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N
|f(x)|>M>|f(0)|>|f(x0)| точка x0 является точкой
минимуа |f(x)| на всей комплексной плоскости.
|f(x0)|=0 т.к по лемме Даламбера если |f(x0)|¹0 то x
0 не точка минимума для |f(x)|Þ x0-корень многочлена
f(x).
Теорема доказана.
Полученое противоречит тому, что M=sup{ f(x)}. Следовательно
функция достигает свего максимума. Аналогично доказывается достижение минимума.
Доказательство основной теоремы.
Пусть дан многочлен f(x), очевидно что если an-свободный член, то
f(0)= an. Теперь применим лемму№3: возьмем М=|f(0)| =|an|
тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Е
ограниченный окружностью с центром в нуле и радиусом N, включая границы круга.
Так как (по лемме №1) многочлен f(x)-непрерывен, то и |f(x)|-непрерывен внутри
замкнутого круга Е, следовательно(по лемме №6), существует такая точка x0
, что для всех x из E выполняется неравенство |f(x)|>=|f(x0)|. x
0 является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N
|f(x)|>M>|f(0)|>|f(x0)| точка x0 является точкой
минимуа |f(x)| на всей комплексной плоскости.
|f(x0)|=0 т.к по лемме Даламбера если |f(x0)|¹0 то x
0 не точка минимума для |f(x)|Þ x0-корень многочлена
f(x).
Теорема доказана.
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



