|
|
| Курсовая: Целочисленное программирование |
Курсовая: Целочисленное программирование
Российский Государственный Торгово-Экономический Университет
Ивановский филиал
Курсовая работа
По теме: «Целочисленное программирование»
Выполнила: студентка 2 курса УФФ
Прозорова В.С.
Проверила: Малеж Л.Н.
Груздева Н.Н.
Иваново 2003г.
План:
Введение.
1.Целочисленное программирование. Общие понятия.
2.Метод Гомори.
3.Метод ветвей и границ.
4.Циклический алгоритм целочисленного программирования.
5.Полностью целочисленный алгоритм.
6.Задача о рюкзаке.
7.Задача о назначении.
8.Задача коммивояжера.
Заключение.
Список используемой литературы.
Ведение.
При рассмотрении целого ряда задач финансового менеджмента и бизнеса необходимо
учитывать требование целочисленности используемых переменных. Такие задачи
называются задачами целочисленного программирования.
Под задачей целочисленного программирования (ЦП) понимается задача, в которой
все или некоторые переменные должны принимать целые значения. В том случае,
когда ограничения и целевая функция задачи представляют собой линейные
зависимости, задачу называют целочисленной задачей линейного
программирования. В противном случае, когда хотя бы одна зависимость будет
нелинейной, это будет целочисленной задачей нелинейного программирования.
Особый интерес к задачам ЦП вызван тем, что во многих практических задачах
необходимо находить целочисленное решение ввиду дискретности ряда значений
искомых переменных.
Целочисленное программирование возникло в 50-60-е годы нашего века из нужд
практики - главным образом в работах американских математиков Дж.Данцига и
Р.Гомори. Первоначально целочисленное программирование развивалось независимо
от геометрии чисел на основе теории и методов математической оптимизации
,прежде всего линейного программирования. Однако, в последние время
исследования в этом направлении все чаще проводятся средствами математики
целых чисел.
Задачи такого типа весьма актуальны, так как к их решению сводится анализ
разнообразных ситуаций , возникающих в экономике, технике, военном деле и
других областях. С появлением ЭВМ, ростом их производительности повысился
интерес к задачам такого типа и к математике в целом.
Целочисленное программирование. Основные понятия.
При рассмотрении целого ряда задач финансового менеджмента и бизнеса необходимо
учитывать требование целочисленности используемых переменных. Такие задачи
называются задачами целочисленного программирования.
Целочисленным (иногда его называют также дискретным) программированием
называется раздел математического программирования, изучающий экстремальные
задачи, в которых на искомые переменные накладывается условие
целочисленности, а область допустимых решений конечна. Огромное количество
экономических задач носит дискретный, чаще всего целочисленный характер, что
связано, как правило с физической неделимостью многих элементов расчета:
например, нельзя построить два с половиной завода, купить полтора автомобиля
и т.д. В ряде случаев такие задачи решаются обычными методами, например,
симплексным методом, с последующим округлением до целых чисел. Однако такой
подход оправдан, когда отдельная единица составляет очень малую часть всего
объема (например, товарных запасов); в противном случае он может внести
значительные искажения в действительно оптимальное решение. Поэтому
разработаны специальные методы решения целочисленных задач.
Рекомендации по формулировке и решению ЦП
- Количество целочисленных переменных уменьшать насколько возможно.
Например, целочисленные переменные, значения которых должно быть не менее
20, можно рассматривать как непрерывные.
- В отличие от общих
задач ЛП, добавление новых ограничений особенно включающих целочисленные
переменные, обычно уменьшают время решения задач ЦП.
- Если нет
острой необходимости в нахождении точного оптимального целочисленного
решения, отличающегося от непрерывного решения, например, 3%. Тогда
реализацию метода ветвей и границ для задачи максимизации можно
заканчивать, если отношение разницы между верхней и нижней границ к
верхней границы меньше 0,03.
Метод ветвей и границ можно применять для решения задач нелинейного
программирования.
Метод Гомори
Задача целочисленного программирования может быть сформулирована следующим
образом: найти максимум или минимум функции
(7.1)
при условиях
(7.2)
Xj > 0, j = 1, 2, ..., n, а также при дополнительном условии
хj — целые числа.
В некоторых случаях условие (7.4) распространяется только на часть переменных,
такие задачи называются частично целочисленными.
Для решения задач целочисленного программирования разработаны специальные
методы. К ним относятся метод отсечений (метод Гомори) и метод ветвей и
границ.
В основе метода Гомори заложена идея, состоящая в том, что сначала решается
задача линейного программирования (7.1)—(7.3) без учета условий
целочисленности. Если полученное таким образом решение целочисленное, то оно
принимается за оптимальный план задачи (7.I)—(7.4). Если решение
нецелочисленное, то система ограничений дополняется условием, которое
отсекает от множества планов задачи нецелочисленный оптимальный план, но при
этом сохраняет целочисленные вершины множества планов. Затем решается задача
линейного программирования с дополнительным условием. Если полученное таким
образом решение целочисленное, то оно оптимально и для задачи (7.1)—(7.4).
Если же и после этого не для всех переменных выполняется условие
целочисленности, то вводится новое условие-отсечение. Условия-отсечения
выбираются таким образом, чтобы за конечное число шагов прийти к
целочисленному решению, если оно у данной задачи существует. Один из
алгоритмов построения таких условий-отсечений был предложен Гомори.
Рассмотрим указанный алгоритм. Пусть получено решение задачи (7.1)-(7.3) без
учета целочисленности и пусть в строке r симплексной таблицы с оптимальным
решением содержится нецелочисленная компонента опорного плана хr0.
В этом случае к условиям (7.1)—(7.3) добавляют условие, порожденное строкой г.
Для составления этого условия-отсечения используем г-е уравнение из последней
симплексной таблицы, содержащей оптимальное решение,
(7.5)
Далее введем понятие целой и дробной частей чисел аr0 и а
rj, для чего запишем эти числа в виде:
Здесь [аr0] и [arj] - целые части, a qt, qr] - дробные части чисел аrj и arj.
Например, 37/3 =12 +1/3, так как [37
/3] = 12, a -s/, = -3 + 1/3„ так как [-8/3] = -3.
Из уравнения (7.5) найдем хr
xr=аr0-
Теперь числа аю и аrj заменим суммами целых и дробных частей:
xr =
Предположим, что все xj - целые числа. Тогда разность
является целым числом.
Чтобы оказалось целым числом и хr, необходима целочисленность разности
Но О<qг<1, 0<grj<1, a
(7.6)
Если допустить, что разность (7.6) больше нуля, то
Однако в этом случае разность (7.6) не может быть целым числом.
Следовательно, условие целочисленности разности может быть обеспечено только
неравенством
(7.7)
Условие (7.7) и является добавочным ограничением в задаче линейного
программирования. Для использования его в симплексном методе требуется ввести
дополнительную переменную хп+≥0 , после чего неравенство
превращается в уравнение
Обычно это ограничение записывают в следующем виде:
(7.8)
Последовательно добавляя новые ограничения к решению очередных задач,
получаем целочисленные координаты оптимального плана задачи (7.1)—(7.4), если
только не выясняется в какой-либо момент, что текущая задача не имеет
решения. Это означало бы отсутствие целочисленного решения задачи
(7.1)—(7.4).
Пример 1. Найти оптимальный целочисленный план задачи Z(X) = х1 - Зх
2 + 5х3 + 2х4 -max
при условия
x1+x2+x3 =15
2x1+ 3x3+x4=8,
хj, > 0, хj — целые числа, j = 1, 2, 3, 4.
Решение. Пошаговое решение задачи приведено в табл. 7.1
Таблица 7.1
Оптимальный план задачи без условия целочисленности
X = (0, 37/3, 8/3, 0)- для дальнейшего решения задачи к таблице оптимального
плана добавлено условие
-2/3x1-1/3x4≤-2/3.
Номер индекса г выбран из условия большей дробной части компоненты аi0
. Имеем г = 2; j = 0: [8/3] = 2, 2 – 8/3 = -2/3; j=1:
[2/31 = О, О - 2/3 =
-2/3; j = 2: [0] = 0, 0 - 0 = 0; j = 3: [0]= 0,
0 - 0 = 0; j = 4: [1/3] = 0, 0 — 1/3 = -1/
3. Сделав один шаг (в общем случае для получения целочисленного решения
одной итерации, конечно, недостаточно) метода последовательного уточнения
оценок, получили оптимальный план целочисленной задачи Х*= (О, 13, 2, 2)
Трудоемкость решения целочисленной задачи обусловлена вводом новых добавочных
ограничений и новых переменных. В связи с этим необходимо придерживаться
следующего правила, позволяющего при определенных условиях сокращать текущие
таблицы. Дополнительная переменная хп+1 вводится в процессе решения
с добавочным ограничением как базисная переменная очередного псевдоплана и
сразу, на этой же итерации, переводится в число небазисных компонент. Если на
дальнейших итерациях, согласно правилу преобразования таблицы, переменная х
п+1 снова окажется базисной, ее значение станет несущественным для
основных переменных задачи, так что строка и столбец текущей таблицы,
отвечающие хп+] вычеркиваются. Правило сокращения таблиц
ограничивает их размеры: не более n строк и не более (2n -m) столбцов.
Рассматриваемый алгоритм целочисленного программирования сводится к методу
последовательного уточнения оценок с дополнительными правилами расширения и
сокращения текущей таблицы решения задачи.
Пример 2. Получить целочисленный оптимальный план задачи
Z(X) = x1— 4х2 — 2х3 + Зх4 —> max при условиях
3x1+x2+8x3+x4=35
x1 +x3+x4≤6
xj≥ 0, хj — целые числа, j = 1, 2, 3, 4.
Решение. Пошаговое решение задачи приведено в табл. 7.2.
Таблица 7.2
На шаге 2 решения задачи без ограничения целочисленности получаем
оптимальный нецелочисленный план
X = (0, 0, 29/7, 13/7).
Поскольку обе базисные координаты X нецелочисленны, выбираем любую — первую
или вторую — строку таблицы на шаге 2, а именно вторую, и строим добавочное
ограничение
-5/7x1-6/7x2-1/7x5+x6=-6/7.
Вводя ограничение добавочной строкой на шаге 2, находим направляющий элемент
в этой строке:
Осуществляя преобразование табл. 7.2 с направляющим элементом (-5/7),
получаем на шаге 3 оптимальный план новой задачи, снова нецелочисленный. На
шаге 3 добавляем очередное условие, получаем четыре строки ограничений.
Поскольку на шаге 3 достигается
в столбце А6, то х6 становится базисной переменной на шаге
4. В соответствии с правилом сокращения таблицы на шаге 4 вычеркиваем строку
и столбец, соответствующие х6, добавляем новую строку, а на шаге 5
получаем псевдоплан X = (4, 0, 3, -1). Методом последовательного уточнения
оценок на шаге 6 получаем план, но нецелочисленный. Оптимальный целочисленный
план получаем лишь на шаге 7: X* = (О, 1, 4, 2), max Z(X) = -6.
Метод ветвей и границ
Одним из широко распространенных методов решения целочисленных задач
является метод ветвей и границ, который может быть использован как для задач
линейного программирования, так и для задач, не сводимых к задачам линейного
программирования. Рассмотрим идею метода ветвей и границ на примере общей
задачи дискретного программирования
f(X) -> max,
(7.9)
Х€D
(7.10)
где D — конечное множество.
Сначала найдем оценку £(D) (границу) функции f(X), X е D: f(X) ≤
£(D) для V X е D. Если для некоторого плана Х° задачи (7.9)-(7.10)
справедливо равенствоf(X0) = £(D), то Х° = X*
является решением задачи. Если указанное условие не выполняется, то возможно
разбиение (ветвление) множества D на конечное число непересекающихся
подмножеств D1i: ỤD1i. = D,
∩D1i = Ө, и вычисление оценки £(D1
i) (границ), 1≤i≤m (рис 7.1)
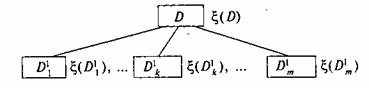Рис. 7.1
Если для некоторого плана X1i е Di1, 1
≤ / ≤ m выполняется условие f(Xkl)= £(D
1k)≥ £(D1i),
1≤i≤m то Xk1=X* является
оптимальным планом (решением) задачи (7.9)-(7.10).
Если такого плана нет, то выбирается подмножество Dkl с
наибольшей оценкой £(D1i):
и разбивается на конечное число непересекающихся подмножеств
D2kj: UD2kj=D1k,
∩D2kj=Ө. Для каждого подмножества находится
оценка £(D2kj), 1≤j≤n (рис 7.2)
(рис. 7.2).
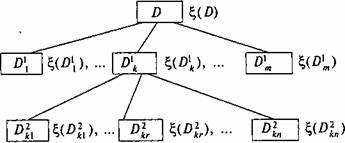Если при этом найдется план X2j е D2kJ
, 1 ≤j ≤n, такой, что f(X2r)= £(D2
kr)≥ £(D2kj), 1≤j≤n, то X
2r= X* является решением задачи (7.9)-(7.10). Если такого плана
нет, то процедуру ветвления осуществляют для множества D2kj
с наибольшей оценкой £(D2kj) , 1≤j≤n .
Способ ветвления определяется спецификой конкретной задачи.
Рассмотрим задачу, которую можно свести к задаче целочисленного линейного
программирования.
Пример.
Контейнер объемом 5 м3 помещен на контейнеровоз грузоподъемностью 12
т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза
mj (в тоннах), объем единицы груза Vj (в м3),
стоимости Cj (в условных денежных единицах) приведены в табл. 7.3.
Таблица 7.3
| Вид груза у | mj | V, | Сj | | 1 | 3 | 1 | 10 | | 2 | 1 | 2 | 12 |
Требуется загрузить контейнер таким образом, чтобы стоимость перевозимого
груза была максимальной.
Решение. Математическая модель задачи имеет вид
Z(X) = 10x1+12x2→max,
(7.11)
3x1+x2≤12,
x1+2x2≤5
x1≥0
(7.12)
x2≥0
x1, x2- целые числа (7.13)
где x1, x2 - число единиц соответственно первого и второго груза.
Множество планов этой задачи обозначим через D - это множество целых точек
многогранника ОАВС (рис. 7.3).
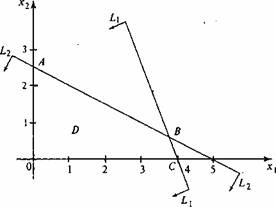Рис. 7.3
Сначала решаем задачу (7.11)—(7.13) без условия целочисленности, получим оценку
множества D - значение функции Z(X) на оптимальном плане Х° = (19/
5, 3/5):
ТочкаXнеявляется оптимальным планом задачи (7.1 1)— (7.13). Поэтому в
соответствии с методом ветвей и границ требуется разбить множество D на
непересекающиеся подмножества. Выберем первую нецелочисленную переменную x
1=19/5=34/5 и разобьем множество D на два непересекающихся подмножества D
11 и D22. Линии x1=3 (L3
) и x4= (L3) являются линиями разбиения.
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|
