[194]

[72,195]

[196]

[197]

[198]

[199]

[200]

Как мы заметили, есть такие числа, которые не являются суммой делителей ни

одного числа и так же есть такие числа, которые являются суммой делителей ни

одного, а нескольких чисел. Теперь посмотрим только те числа, которые

являются суммой делителей ни одного, а нескольких чисел:

[6,12], [11,12]

[10,18], [17,18]

[14,24], [15,24], [23,24]

[16,31]. [25,31]

[21,32], [31,32]

[20, 42], [26,42], [41,42]

[33,48], [35,48], [47,48]

[34,5 4], [53,54]

[28,56], [39,56]

[24,60], [38,60], [59, 60]

[30,72], [46,72], [51,72], [55,72], [71,72]

[57,80], [79,80]

[44,84], [65,84], [83,84]

[40,90], [58, 9 0], [89,90]

[42,96], [62,96], [69,96], [77,96]

[52,98], [97,98]

[54,120], [56, 120], [87,120], [95,120]

[48,124], [75,124]

[68,126], [82,126]

[66,144], [70, 144], [94,144]

[60,168], [78,168], [92,168]

Отсюда можно сделать вывод, что нахождение числа по его сумме делителей не

всегда возможно и не всегда однозначно.

Теперь построим график. По оси Х расположим числа, а по оси Y их сумму

делителей (числа от 1 до 1000):

Посмотрим, что же у нас получилось: на графике отчётливо просматриваются

несколько прямых линий, например, нижняя это – простые числа. Верхняя граница –

это наиболее сложные числа (имеющие наибольшее количество делителей) - это не

прямая, но и не парабола. Скорее всего, – это показательная функция (у = а

х).

В мемуарах Эйлера я нашел много интересных мне рассуждений(σ(n) – сумма

делителей числа n): Определив значение σ(n) мы ясно видим, что если p –

простое, то σ(p)= p + 1. σ(1)=1, а если число n – составное, то

σ(n)>1 + n.

Если a, b, c, d – различные простые числа, то мы видим:

σ(ab)=1+a+b+ab=(1+a)(1+b)= σ(a)σ(b)

σ(abcd)= σ(a)σ(b)σ(c)σ(d)

σ(a^2)=1+a+a2=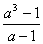

σ(a^3)=1+a+a2+a3=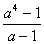

И вообще

σ(nn)=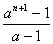

Пользуясь этим:

σ(aqbwcedr)= σ(aq)σ(bw)σ(ce)σ(dr)

Например σ(360), 360 = 23*32*5 => σ(23

) σ(32) σ(5)=15*13*6=1170.

Чтобы показать последовательность сумм делителей приведём таблицу:

n	0	1	2	3	4	5	6	7	8	9
0	-	1	3	4	7	6	12	8	15	13
10	18	12	28	14	24	24	31	18	39	20
20	42	32	36	24	60	31	42	40	56	30
30	72	32	63	48	54	48	91	38	60	56
40	90	42	96	44	84	78	72	48	124	57
50	93	72	98	54	120	72	120	80	90	60
60	168	62	96	104	127	84	144	68	126	96
70	144	72	195	74	114	424	140	96	168	80
80	186	121	126	84	224	108	132	120	180	90
90	234	112	168	128	144	120	252	98	171	156

Если σ(n) обозначает член любой этой последовательности, а σ(n -

1), σ(n - 2), σ(n - 3). предшествующие члены, то σ(n) всегда

можно получить по нескольким предыдущим членам:

σ(n) = σ(n - 1) + σ(n - 2) - σ(n - 5) - σ(n - 7) +

σ(n - 12) + σ(n - 15) - σ(n - 22) - σ(n – 26) + . (**)

Знаки «+» «-» в правой части формулы попарно чередуются. Закон чисел 1, 2, 5,

7, 12, 15.,которые мы должны вычитать из рассматриваемого числа n, станет

ясен если мы возьмем их разности:

Числа:1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100.

Разности: 1, 3, 2, 5, 3, 7, 4, 9, 5, 11, 6, 13, 7, 15, 8.

В самом деле, мы имеем здесь поочередно все целые числа 1, 2, 3, 4, 5, 6, 7.

и нечетные 3, 5, 7,9 11.

Хотя эта последовательность бесконечна, мы должны в каждом случае брать

только те члены, для которых числа стоящие под знаком σ, еще

положительны, и опускать σ для отрицательных чисел. Если в нашей формуле

встретиться σ(0), то, поскольку его значение само по себе является

неопределённым, мы должны подставить вместо σ(0) рассматриваемое число

n. Примеры:

σ(1) = σ(0) =1

= 1

σ(2) = σ(1) + σ(0) =

1 + 2 = 3

.

σ(20) = σ(19)+σ(18)-σ(15)-

σ(13)+9σ(8)+σ(5)=20+39-24-14+15+6= 42

Доказательство теоремы (**) я приводить не буду.

Вообще, найти сумму всех делителей числа можно с помощью канонического

разложения натурального числа (это уже было сказано выше). Сумму делителей

числа n обозначают σ(n). Легко найти σ(n) для небольших

натуральных чисел, например σ(12) = 1+2+3+4+6+12=28(это было приведено

выше). Но при достаточно больших числах отыскивание всех делителей, а тем

более их суммы становится затруднительным. Совсем другое дело, если уже

известно, что каноническое

разложение числа n таково:.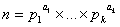

Его делителями являются все числа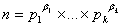

, для которых 0 ≤ βs ≤ αs, s = 1, .,

k. Ясно, что σ(n) представляет собой сумму всех таких чисел при различных

значениях показателей

β1, β2, . βk. Этот результат мы

получим раскрыв скобки в произведении

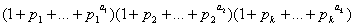
По формуле конечного числа членов геометрической прогрессии приходим к равенству

(*)

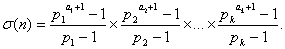По этой формуле σ(360) = .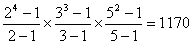

Формулу для вычисления значения функции σ(n) вывел замечательный

английский математик Джон Валлис(1616 - 1703) – один из основателей и первых

членов Лондонского Королевства общества (Академии наук). Он был первым из

английских математиков, начавших заниматься математическим анализом. Ему

принадлежат многие обозначения и термины, применяемые сейчас в математике, в

частности знак ∞ для обозначения бесконечности. Валлис вывел

удивительную формулу, представляющую число π в виде бесконечного

произведения:

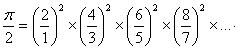
Д. Валлис много занимался комбинаторикой и её приложениями к теории шифров,

не без основания считая себя родоначальником новой науки – криптологии (от

греч. «криптос» - тайный, «логос» - наука, учение). Он был одним из лучших

шифровальщиков своего времени и по поручению министра полиции Терло занимался

в республиканском правительстве Кромвеля расшифровкой посланий монархических

заговорщиков.

С функцией σ(n) связан ряд любопытных задач. Например:

1.) Найти пару целых чисел, удовлетворяющих условию: σ(m1)=m

2, σ(m2)=m1.

Некоторые из них не удаётся решить даже с использованием формулы (*). Так,

например, не иначе как подбором можно найти числа, для которых σ(n) есть

квадрат некоторого натурального числа. Такими числами являются 22, 66, 70,

81, 343, 1501, 4479865. Вот ещё две задачи, приведённые в 1657 г. Пьером

Ферма:

1.) найти такое m, для которого σ(m3) – квадрат натурального

числа (Ферма нашёл не одно решение этой задачи);

2.) найти такое m, для которого σ(m2) – куб натурального числа.

Например, одним из решений первой задачи является m = 7, а для второй m = 43098.

С помощью программы Derive, я попробовал найти ещё решения и у меня этого не

получилось. (я рассматривал σ(m3) = n2, где m

принимает значения от 1 до 1000, а n от 1 до 5000 в 1.) и тоже самое в 2.) )

Формулы:

1. DELITELI(m) := SELECT(MOD(m, n) = 0, n, 1, m)

DIMENSION(DELITELI(m))

2. SUMMADELITELEY(m) := Σ

ELEMENT(DELITELI(m), i)

i=1

Страницы: 1, 2, 3, 4, 5, 6, 7