|
|
| Лекция: Конспект лекций по дискретной математике |
Для полностью определенной булевой функции количество меток в каждой строке
равно числу ноль - кубов покрываемых кубом данной строки .Для не полностью
определенной функции количество меток в строке зависит от количества
безразличных наборов покрываемых данным кубом .Для нахождения кубов
,принадлежащих ядру покрытия в таблице ищутся столбцы с единственной меткой
.Строка ,которой принадлежит эта метка определяет куб ядра .
Т(f)={1XX0}
3) Определение множества минимальных покрытий .
На этом этапе из множества максимальных кубов не принадлежащих ядру покрытия
,выделяются такие минимальные подмножества ,с помощью каждого из которых
покрываются оставшиеся вершины (не покрытые ядром) .
Реализацию этого этапа целесообразно производить с использованием упрощенной
таблицы.
В упрощенной таблице вычеркнуты все кубы принадлежащие ядру и вершины
покрываемые ядром.
Для решения задачи 3-го этапа можно использовать один из 3-х методов или их
комбинацию:
1) Метод простого перебора
2) Метод Петрика
3) Дальнейшее упрощение.
1)На данном этапе целесообразно ввести обозначение максимальных кубов и
существенных вершин.
Максимальные кубы обозначены в таблице А...F
1-ый метод целесообразно применять для упрощенной таблицы небольшого объема
.Этот метод не дает гарантии получения всех максимальных покрытий.
Для нашего примера все кубы входящие в упрощенную таблицу покрытий обладают
одной размерностью(то есть необходимо выбрать минимальное количество этих
кубов для покрытия всех оставшихся существенных вершин).
Из таблицы видно ,что минимальное число кубов равно трем.К возможным
вариантам покрытий относятся:
ì Tü ì Tü
C min1(f)= êAú C min 1(f)= êBú ,...
ïCú êCú
îE þ îE þ
2)Достоинство этого метода-получение всех минимальных покрытий.
Метод базируется на составлении логического выражения , представляющего собой
условие покрытия всех вершин из упрощенной таблицы покрытий и преобразования
этого выражения .
Y=(AvB)(AvC)(CvD)(DvE)(EvF)=(AvBC)(DvCE)(EvF)=
=(AvBC)(DEvCEvDFvCEF)=
=(ADEvACEvADFvBCDEvBCEvBCDF)
Каждый из пяти конъюнктивных термов соответствует покрытию булевой функции(с
учетом дополнения ядром),каждому из которых можно поставить в соответствие
тупиковую ДНФ.
Последний терм не соответствует минимальному покрытию ,то есть данная функция
имеет четыре минимальных покрытия.
3) Дальнейшее упрощение состоит в применение двух операций : а)Вычеркивание
лишних строк.
б)Вычеркивание лишних столбцов.
Если множество меток i-й строки является подмножеством меток j-й строки и куб
i имеет небольшую размерность, чем куб j, то из таблицы можно вычеркнуть i-ю
строку так как существенные вершины покрываемые i-м кубом будут с гарантией
покрыты j-м кубом.
В дальнейшем рекомендуется построить новую упрошенную таблицу.
В отношении новой таблицы можно использовать один из трех методов: 1)
Метод простого перебора.
2)Метод Петрика.
3)Дальнейшее упрощение.
Функциональная полнота системы булевых функций.
Система булевых функций S={y1,y2,...,ym
}называется функционально полной ,если с помощью функций этой системы можно
выразить любую сколь угодно сложную булеву функцию с использованием метода
суперпозиции, возможно многократно.
Под суперпозицией в отношении булевых функций понимается подстановка одних
функций в другие вместо их аргумента.
Примерами полных систем являются :
1)S1 ={ù,&,Ú}(булев базис)
Обоснованность утверждения о функциональной полноте этой системы базируется
на возможности представления любой булевой функции в нормальной форме
,которая является комбинацией операций отрицания ,конъюнкции и дизъюнкции,
применительно к аргументу этой функции.
Система S1 ={ù,&,Ú} является избыточной так как из
нее можно удалить одну из функций (& или Ú) без нарушения
функциональной полноты.
Получаемые при этом системы S2 ={ù,&} и S3
{ù,&,Ú}обычно называют сокращенным булевым базисом .
Недостающие операции( Ú в системе S2 и & в системе S3
) могут быть выражены с помощью следствий из законов
____
Де Моргана : x1V x2= 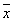 1 1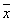 2
_____
x1 x2= 2
_____
x1 x2= 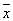 1 v 1 v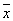 2
Функциональная полнота системы булевых функций называется минимальной ,если
удаление из нее какой-либо функции приводит к нарушению свойства
функциональной полноты.
Системы из одной функции S4=¯(стрелка Пирса)
S5=|(штрих Шеффера)
которые принято называть универсальным базисом.
2)Базис Жегалкина S6= {&, Å, 1}
Понятие функциональной полноты системы булевых функций связано с аналогичным
понятием для системы логических элементов.
Эта связь заключается в следующем :
Если каждой функции из некоторой функционально полной системы сопоставить
логический элемент, реализующий эту функцию ,то система логических элементов
соответствующая некоторой функционально полной системе булевых функций
естественным образом оказывается тоже функционально полной .
Задача синтеза комбинационных схем с использованием функционально полной
системы логических элементов можно построить комбинационную схему реализующую
любую наперед заданную ,сколь угодно сложную булеву функцию.
Доказательство функциональной полноты некоторой системы
булевых функций можно осуществлять одним из двух способов:
1) С использованием теоремы о функциональной полноте .
2) С использованием конструктивного подхода .
Теорема о функциональной полноте (Пост - Яблонского).
Для того, чтобы система булевых функций была функционально полной необходимо
и достаточно чтобы она содержала хотя бы одну функцию не:
1) cохраняющую константу ноль
2) cохраняющую константу единица
3) линейную функцию
4) монотонную функцию
5) самодвойственную функцию.
Замечательные классы булевых функций.
1. Булева функция называется сохраняющей константу ноль , если на нулевом
наборе аргументов она принимает значение равное нулю, то есть f(0,0,0,...,0)
= 0;
В противном случае функция относится к классу не cохраняющих константу ноль.
К функциям ,сохраняющим константу ноль относятся
f(x1,x2)= x1 v x2
f(x1,x2)= x1 * x2
К функциям не cохраняющим константу ноль относятся
f(x)= 2
Функциональная полнота системы булевых функций называется минимальной ,если
удаление из нее какой-либо функции приводит к нарушению свойства
функциональной полноты.
Системы из одной функции S4=¯(стрелка Пирса)
S5=|(штрих Шеффера)
которые принято называть универсальным базисом.
2)Базис Жегалкина S6= {&, Å, 1}
Понятие функциональной полноты системы булевых функций связано с аналогичным
понятием для системы логических элементов.
Эта связь заключается в следующем :
Если каждой функции из некоторой функционально полной системы сопоставить
логический элемент, реализующий эту функцию ,то система логических элементов
соответствующая некоторой функционально полной системе булевых функций
естественным образом оказывается тоже функционально полной .
Задача синтеза комбинационных схем с использованием функционально полной
системы логических элементов можно построить комбинационную схему реализующую
любую наперед заданную ,сколь угодно сложную булеву функцию.
Доказательство функциональной полноты некоторой системы
булевых функций можно осуществлять одним из двух способов:
1) С использованием теоремы о функциональной полноте .
2) С использованием конструктивного подхода .
Теорема о функциональной полноте (Пост - Яблонского).
Для того, чтобы система булевых функций была функционально полной необходимо
и достаточно чтобы она содержала хотя бы одну функцию не:
1) cохраняющую константу ноль
2) cохраняющую константу единица
3) линейную функцию
4) монотонную функцию
5) самодвойственную функцию.
Замечательные классы булевых функций.
1. Булева функция называется сохраняющей константу ноль , если на нулевом
наборе аргументов она принимает значение равное нулю, то есть f(0,0,0,...,0)
= 0;
В противном случае функция относится к классу не cохраняющих константу ноль.
К функциям ,сохраняющим константу ноль относятся
f(x1,x2)= x1 v x2
f(x1,x2)= x1 * x2
К функциям не cохраняющим константу ноль относятся
f(x)=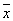 и f(x1,x2)=x1~x2
2.Булева функция называется сохраняющей константу единица , если на единичном
наборе аргументов она принимает значение равное единице, то есть
f(1,1,1,...,1)= 1;
В противном случае функция относится к классу не cохраняющих константу единица.
К функциям ,сохраняющим константу единица относятся
f(x1,x2)= x1 v x2
f(x1,x2)= x1 * x2
К функциям не cохраняющим константу единица относятся
f(x)= и f(x1,x2)=x1~x2
2.Булева функция называется сохраняющей константу единица , если на единичном
наборе аргументов она принимает значение равное единице, то есть
f(1,1,1,...,1)= 1;
В противном случае функция относится к классу не cохраняющих константу единица.
К функциям ,сохраняющим константу единица относятся
f(x1,x2)= x1 v x2
f(x1,x2)= x1 * x2
К функциям не cохраняющим константу единица относятся
f(x)=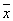 и f(x1,x2)=x1Åx2
3. Булева функция называется линейной если она представима полиномом
Жегалкина первой степени.
В булевой алгебре доказывается теорема о возможности представления любой
булевой функции от n переменных с помощью полинома Жегалкина n-ой степени.
В общем случае полином имеет вид :
fn (x) = K0 ÅK1x1 Å...ÅKn xn Å...
...ÅKn+1x1x2 ÅKn+2x1x3 Å...ÅKn+lxn-1xn Å...
...
...ÅKn+mx1x2...xn
K0 ,K1 ,Kn+m -являются коэффициентами и
представляют собой логические константы нуля или единицы.
В алгебре Жегалкина одноименной полином можно считать канонической нормальной
формой для булевой алгебры.
Полином Жегалкина является линейным (1-ой степени) если все коэффициенты общего
полинома ,начиная с Kn+1=Kn+2 =...=Kn+m =0
В отношении функции от 2-х переменных полином Жегалкина имеет вид (линейный): f
2(x)=K0ÅK1x1ÅK2x
2
Примерами линейных функций являются:
y= x1Åx2 (K0=0,K1=K2=1)
_____
y= x1~x2=x1Åx2=1Åx1Åx2 (K0=K1=K2)
y= и f(x1,x2)=x1Åx2
3. Булева функция называется линейной если она представима полиномом
Жегалкина первой степени.
В булевой алгебре доказывается теорема о возможности представления любой
булевой функции от n переменных с помощью полинома Жегалкина n-ой степени.
В общем случае полином имеет вид :
fn (x) = K0 ÅK1x1 Å...ÅKn xn Å...
...ÅKn+1x1x2 ÅKn+2x1x3 Å...ÅKn+lxn-1xn Å...
...
...ÅKn+mx1x2...xn
K0 ,K1 ,Kn+m -являются коэффициентами и
представляют собой логические константы нуля или единицы.
В алгебре Жегалкина одноименной полином можно считать канонической нормальной
формой для булевой алгебры.
Полином Жегалкина является линейным (1-ой степени) если все коэффициенты общего
полинома ,начиная с Kn+1=Kn+2 =...=Kn+m =0
В отношении функции от 2-х переменных полином Жегалкина имеет вид (линейный): f
2(x)=K0ÅK1x1ÅK2x
2
Примерами линейных функций являются:
y= x1Åx2 (K0=0,K1=K2=1)
_____
y= x1~x2=x1Åx2=1Åx1Åx2 (K0=K1=K2)
y= 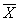 =1Åx1 (K0=K1=1 ,K2=0)
Примеры нелинейных функций:
y= x1*x2
____
y= x1lx2 =x1*x2=1Åx1*x2
4.Булева функция называется монотонной если при возрастании наборов
аргументов она принимает неубывающие значения.
A=(a1,a2,...,an)>B=(b1,b2,...,bn)
f(A)³f(B)
Между наборами аргументов А и В имеет место отношение возрастания в том и
только том случае , если имеет место отношение не убывания для всех компонент
этого набора:
___
ai³bi (i=1, n )
и по крайней мере для одной компоненты имеет место отношение возрастания.
Примеры наборов ,для которых имеет место отношение возрастания: (1011)>(0011)
(1011)>(0001)
(0001)>(0000)
Пример несопоставимых наборов (1011) и (0111)
В отношении функции от 2-х переменных несопоставимыми являются наборы (01) и
(10)
Пример немонотонных функций: y= =1Åx1 (K0=K1=1 ,K2=0)
Примеры нелинейных функций:
y= x1*x2
____
y= x1lx2 =x1*x2=1Åx1*x2
4.Булева функция называется монотонной если при возрастании наборов
аргументов она принимает неубывающие значения.
A=(a1,a2,...,an)>B=(b1,b2,...,bn)
f(A)³f(B)
Между наборами аргументов А и В имеет место отношение возрастания в том и
только том случае , если имеет место отношение не убывания для всех компонент
этого набора:
___
ai³bi (i=1, n )
и по крайней мере для одной компоненты имеет место отношение возрастания.
Примеры наборов ,для которых имеет место отношение возрастания: (1011)>(0011)
(1011)>(0001)
(0001)>(0000)
Пример несопоставимых наборов (1011) и (0111)
В отношении функции от 2-х переменных несопоставимыми являются наборы (01) и
(10)
Пример немонотонных функций: y=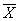 y= x1Åx2
5.Две булевы функции fn(x) и gn(x) называются
двойственными если для любых наборов аргументов выполняется равенство
____
fn(x) =gn(x) то есть функции f и g на противоположных
наборах аргументов х и
y= x1Åx2
5.Две булевы функции fn(x) и gn(x) называются
двойственными если для любых наборов аргументов выполняется равенство
____
fn(x) =gn(x) то есть функции f и g на противоположных
наборах аргументов х и 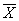 принимает противоположные значения .
Два набора аргументов называются противоположными если любая из их компонент
принимает противоположные значения.
x=(0101)
принимает противоположные значения .
Два набора аргументов называются противоположными если любая из их компонент
принимает противоположные значения.
x=(0101) 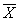 =(1010)
Булева функция называется самодвойственной если она является двойственной по
отношению к самой себе то есть принимает противоположные значения на
противоположных наборах аргументов.
Примером самодвойственной функции является : у= =(1010)
Булева функция называется самодвойственной если она является двойственной по
отношению к самой себе то есть принимает противоположные значения на
противоположных наборах аргументов.
Примером самодвойственной функции является : у= 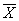 Примеры не самодвойственных функций: у=х1*х2
у=х1vх2
у=х1Åх2
Принадлежность базовых булевых функций и логических констант к замечательным
классам представлена таблицей.
К0 + сохраняет константу ноль ,- не сохраняет константу ноль
К1 + сохраняет константу единица ,- не сохраняет константу
Кл + линейная ,- нелинейная
Км + монотонная , - не монотонная
Кс + самодвойственная ,- не самодвойственная
Примеры не самодвойственных функций: у=х1*х2
у=х1vх2
у=х1Åх2
Принадлежность базовых булевых функций и логических констант к замечательным
классам представлена таблицей.
К0 + сохраняет константу ноль ,- не сохраняет константу ноль
К1 + сохраняет константу единица ,- не сохраняет константу
Кл + линейная ,- нелинейная
Км + монотонная , - не монотонная
Кс + самодвойственная ,- не самодвойственная
| Функция | К0 | К1 | Кл | Км | Кс | | 0 | + | - | + | + | - | | 1 | - | + | + | + | - | 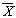
| - | | | | | х1*х2 | + | + | - | + | - | х1vх2 | + | + | | + | - | х1Åх2 | + | - | + | - | - | х1~х2 | - | | + | | - | х1Dх2 | + | | | - | | х1®х2 | - | | | | | х1|х2 | - | | - | | | х1¯х2 | - | | | | |
Страницы: 1, 2, 3, 4
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



