|
|
| Лекция: Конспект по дискретной математики |
Лекция: Конспект по дискретной математики
Дискретная математика
Введение
Общество 21в. – общество информационное. Центр тяжести в решении задач
переместился от задач вычислительной математики к задачам на дискретных
структурах. Математика нужна не как метод расчета, а как метод мышлению
средство формирования и организации.
Такое владение математикой богатой культуры, понимание важности точных
формулировок.
В дисциплине мало методов, но много определений и терминов. В основе
дискретной математике 4 раздела:
1. Язык дискретной математики;
2. Логические функции и автоматы;
3. Теория алгоритмов;
4. Графы и дискретные экстремальные задачи.
Теория алгоритмов и формальных систем является центральной в дисциплине. В
настоящие время от нее возникли ответвления, например, разработка
алгоритмических языков программирования.
Одной из важнейших проблем в дискретной математики является проблема
сложности вычислений.
Теория сложности вычислений помогает оценить расход времени и памяти при
решении задач на ЭВМ. Теория сложности позволяет выделить объективно сложные
задачи (задачи перебора) и неразрешимые задачи.
Мы будем заниматься решением задач реальной размерности с учетом
ограниченности временных и емкостных ресурсов ЭВМ.
Множества и операции над ними
Одно из основных понятий математики – множество.
Определение:
Множеством называется совокупность, набор предметов, объектов или элементов.
Множество обозначают: M,N ...
m1, m2, mn – элементы множества.
Символика
A Î M – принадлежность элемента к множеству;
А Ï М – непринадлежность элемента к множеству.
Примеры числовых множеств:
1,2,3,. множество натуральных чисел N;
.,-2,-1,0,1,2,. - множество целых чисел Z.
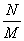 множество рациональных чисел а.
I – множество иррациональных чисел.
R – множество действительных чисел.
K – множество комплексных чисел.
Множество А называется подмножеством В, если всякий элемент А является
элементом В.
А Í В – А подмножество В (нестрогое включение)
Множества А и В равны, если их элементы совпадают.
A = B
Если А Í В и А ¹ В то А Ì В (строгое включение).
Множества бывают конечные и бесконечные.
|М| - мощность множества (число его элементов).
Конечное множество имеет конечное количество элементов.
Пустое множество не содержит элементов: M = Æ.
Пример: пустое множество:
1) множество действительных корней уравнения x2+1=0 пустое: M = Æ.
2) множество D, сумма углов которого ¹ 1800 пустое: M = Æ.
Если дано множество Е и множество и мы рассматриваем все его подмножества, то
множество Е называется униварсельным.
Пример: Если за Е взять множество книг то его подмножества:
художественные книги, книги по математике, физики, физики .
Если универсальное множество состоит из n элементов, то число подмножеств = 2n.
Если множество рациональных чисел а.
I – множество иррациональных чисел.
R – множество действительных чисел.
K – множество комплексных чисел.
Множество А называется подмножеством В, если всякий элемент А является
элементом В.
А Í В – А подмножество В (нестрогое включение)
Множества А и В равны, если их элементы совпадают.
A = B
Если А Í В и А ¹ В то А Ì В (строгое включение).
Множества бывают конечные и бесконечные.
|М| - мощность множества (число его элементов).
Конечное множество имеет конечное количество элементов.
Пустое множество не содержит элементов: M = Æ.
Пример: пустое множество:
1) множество действительных корней уравнения x2+1=0 пустое: M = Æ.
2) множество D, сумма углов которого ¹ 1800 пустое: M = Æ.
Если дано множество Е и множество и мы рассматриваем все его подмножества, то
множество Е называется униварсельным.
Пример: Если за Е взять множество книг то его подмножества:
художественные книги, книги по математике, физики, физики .
Если универсальное множество состоит из n элементов, то число подмножеств = 2n.
Если 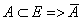 , состоящее из элементов E, не принадлежащих А, называется дополненным.
Множество можно задать:
1) Списком элементов {a,b,c,d,e};
2) Интервалом 1<x<5;
3) Порождающей процедурой: xk=pk sinx=0; , состоящее из элементов E, не принадлежащих А, называется дополненным.
Множество можно задать:
1) Списком элементов {a,b,c,d,e};
2) Интервалом 1<x<5;
3) Порождающей процедурой: xk=pk sinx=0;
Операции над множествами
1) Объединение множеств А и В (союз или). Множество, состоящие из
элементов, которые принадлежат хотя бы одному из множеств А или В называется
объединенным.
А È В
Отношение множеств наглядно иллюстрируется с помощью диаграмм Венна.
Диаграмма Венна – это замкнутая линия, внутри которой расположены
элементы множества.
Объединение двух множеств 
 Объединение системы множеств можно записать
Объединение системы множеств можно записать
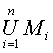 - объединение системы n множеств.
Пример: объединение множеств, когда они
заданы списком.
A = {a,b,d} B = {b,d,e,h} AUB = {a,b,c,d,e,h} - объединение системы n множеств.
Пример: объединение множеств, когда они
заданы списком.
A = {a,b,d} B = {b,d,e,h} AUB = {a,b,c,d,e,h}
| Объединение трех множеств: |
|
2) Пересечением множеств А и В называется множество, состоящие из элементов
принадлежащих одновременно множествам А и В.
 A ÇB
A ÇB
Пересечение прямой и плоскости
1) 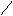 если прямые || пл., то множество пересечений – единственная точка;
2) если прямые II пл., то M ¹Æ;
3) если прямые совпадают, то множество пересечений = множество прямой.
Пересечение системы множеств: если прямые || пл., то множество пересечений – единственная точка;
2) если прямые II пл., то M ¹Æ;
3) если прямые совпадают, то множество пересечений = множество прямой.
Пересечение системы множеств:  4) Разностью 2-х множеств А и В называется множество, состоящее из всех
элементов А, не входящих в В.
С = А \ В
4) Разностью 2-х множеств А и В называется множество, состоящее из всех
элементов А, не входящих в В.
С = А \ В
  A \ B A \ B
 А \ В А \ В
  
 A = {a,b,d}; B = {b,c,d,h} C = A \ B={a}.
В отличии от предыдущих операций разность: 1) строго двухместна;
2) не коммутативна, т.е. A\B ¹ B\A.
4) дополнение
A = {a,b,d}; B = {b,c,d,h} C = A \ B={a}.
В отличии от предыдущих операций разность: 1) строго двухместна;
2) не коммутативна, т.е. A\B ¹ B\A.
4) дополнение  E – универсальное множество.
E – универсальное множество.
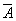 -- дополнение
Операции объединения, пересечения и дополнения называются Булевыми.
Основные законы операций над множествами.
Некоторые свойства È, Ç похожи на алгебраические операции,
однако многие свойства операций над множествами все же отличаются. -- дополнение
Операции объединения, пересечения и дополнения называются Булевыми.
Основные законы операций над множествами.
Некоторые свойства È, Ç похожи на алгебраические операции,
однако многие свойства операций над множествами все же отличаются.
Основные свойства
1) AUB=BUA; AÇB=BÇA – переместительный закон объединения и пересечения.
2) (АUB)UC = AU(BUC); (AÇB)ÇC=AÇ(BÇC) – сочетательный закон.
3) АUÆ=A, AÇÆ=Æ, A \ Æ=A, A \ A=Æ
1,2,3 – есть аналог в алгебре.
3.а) Æ \ A = Æ - нет аналога.
4) 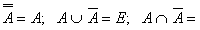 Æ; E \ A = Æ; E \ A =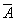 ; A \ E=Æ; AUA=A; AÇA=A; AUE=E; AÇE=A;
5.а) свойства 1-4 очевидны и не нуждаются в доказательствах.
5) AÇ(BUC)=(AÇB)(AÇC) – есть аналогичный
распределительный закон Ç относительно U. ; A \ E=Æ; AUA=A; AÇA=A; AUE=E; AÇE=A;
5.а) свойства 1-4 очевидны и не нуждаются в доказательствах.
5) AÇ(BUC)=(AÇB)(AÇC) – есть аналогичный
распределительный закон Ç относительно U.
Прямые произведения и функции
Прямым декартовым “х” множеством А и В называется множество всех пар (a;b),
таких, что аÎА, bÎB.
С=AхВ, если А=В то С=А2.
Прямыми «х» n множеств A1x,.,xAn называется множество
векторов (a1,.an) таких, что a1ÎA1
,., AnÎAn.
Через теорию множеств введем понятие функции.
Подмножество FÎMx x My называется функцией, если для
каждого элемента хÎMx найдется yÎМу не более
одного.
(x;y)ÎF, y=F(x).
Соответствие между аргументом и функцией можно изобразить с помощью диаграммы
Венна:
Определение: Между множествами MX и MY установлено
взаимноодназночное соответствие, если каждому хÎMX
соответствует 1 элемент yÎMY и обратное справедливо.
Пример: 1) (х,у) в круге
2) x = sinx
Rà R  Пусть даны две функции f: AàB и g: BàC, то функция y:AàC
называется композицией функций f и g.
Y=f o g o – композиция.
Способы задания функций:
1) таблицы, определены для конечных множеств;
2) формула;
3) графики;
Способы 1-3 частные случаи выч. процедуры.
Пример процедуры, не относящейся к 3 способам задания функций n!
Взаимнооднозначное соответствие и мощности множеств.
Определение: Множества равномощны |A|=|B| если между ними
взаимнооднозначное соответствие.
Теорема: Если для конечного множества А мощность равна |A| то количество
всех подмножеств 2|A|=2n.
Множества равномощные N называются счетными, т.е. в них можно выполнить
нумерацию элементов. N – множество натуральных чисел.
Множество N2 – счетно.
Пусть даны две функции f: AàB и g: BàC, то функция y:AàC
называется композицией функций f и g.
Y=f o g o – композиция.
Способы задания функций:
1) таблицы, определены для конечных множеств;
2) формула;
3) графики;
Способы 1-3 частные случаи выч. процедуры.
Пример процедуры, не относящейся к 3 способам задания функций n!
Взаимнооднозначное соответствие и мощности множеств.
Определение: Множества равномощны |A|=|B| если между ними
взаимнооднозначное соответствие.
Теорема: Если для конечного множества А мощность равна |A| то количество
всех подмножеств 2|A|=2n.
Множества равномощные N называются счетными, т.е. в них можно выполнить
нумерацию элементов. N – множество натуральных чисел.
Множество N2 – счетно.
Доказательство
Разобьем N2 на классы
  К 1-ому классу отнесем N1 (1; 1) К 1-ому классу отнесем N1 (1; 1)
| | | | | | 1-ый элемент 1-го множества |
| | 1-ый элемент 2-го множества |
|
Ко 2-му классу N2 {(1;2), (2;1)}
К i-му классу Ni (a+b=i+1
Каждый класс будет содержать i пар.
Упорядоченный классы по возрастанию индекса i, а пары внутри класса
упорядоченные по направлению первого элемента а.
Занумеруем последовательность классов, что и доказывает счетность множества N2.
Аналогично доказывается счетность множеств N3,.,Nk.
Теорема Кантора:
Множество всех действительных чисел на отрезке [0;1] не является счетным.
Доказательство
Допустим это множество счетно изобразим его числа десятичными дробями.
 1-я 0, a11, a12 ..
2-я 0, а21, a22 ..
........
Возьмем произвольное число 0,b1,b2,b3 1-я 0, a11, a12 ..
2-я 0, а21, a22 ..
........
Возьмем произвольное число 0,b1,b2,b3
 b1 ¹ a11, b2 ¹ a22, .
Эта дробь не может выйти в последовательность т.к. отличается от всех
чисел, значит нельзя пронумеровать числа на отрезке [0;1].
Множество нечетно и называется континуальным, а его мощность континуум.
Метод, используемый при доказательстве, называется диагональным методом Кантора. b1 ¹ a11, b2 ¹ a22, .
Эта дробь не может выйти в последовательность т.к. отличается от всех
чисел, значит нельзя пронумеровать числа на отрезке [0;1].
Множество нечетно и называется континуальным, а его мощность континуум.
Метод, используемый при доказательстве, называется диагональным методом Кантора.
Отношение
Пусть дано RÍMn – n местное отношение на множество М.
Будем изучать двухместные или бинарные отношения. Если а и b находятся в
отношении R, то записывается а R b.
Проведем отношение на множество N:
А) отношение £ выполняется для пар (7,9) (7,7_
Б) (9,7) не выполняется.
Пример отношения на множество R
А) отношение находится на одинаковом расстоянии от начала координат
выполняется для пар (3; 4) и (2; Ö21)
Б) (3; 4) и (1; 6) не выполняется.
Для задания бинарных отношений можно использовать любые способы задания
множеств.
Для конечных множеств используют матричный способ задания множеств.
Матрица бинарного отношения на множество M={1;2;3;4}, тогда матрица отношения
С равна
| С= | | 1 | 2 | 3 | 4 | | 1 | 1 | 1 | 1 | 1 | | 2 | 0 | 1 | 1 | 1 | | 3 | 0 | 0 | 1 | 1 | | 4 | 0 | 0 | 0 | 1 |
Отношение Е заданные единичной матрицей
называется отношением равенства.
Отношением назовется обратным к отношением R, если ajRai
тогда и только тогда, когда ajRai обозначают R-1
.
Свойства отношений - Если aRa ==> очн. рефлексивное и
матрица содержит на главной диагонали единицу
если ни для какого а не . ==> отношение антирефлексивное
главная диагональ содержит нули
Пр. отношнний
£ рефлексивное
< антирефлексивное
2. Если из aRb следует bRa, ==> отношение R симметричное. В матрице
отношения элементы
сумм Cij=Cji. Если из aRb и bRa следует a=b ==> отношение R – антисимметричное.
Пр. Если а £ b и b £ a ==> a=b
- Если дано " a,b,c из aRb и aRc следует aRC ==> отношение
называемое транзитивным.
- Отношение называется отношением
эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Пр. отношение равенства E
5. Отношение называется отношением нестрогого порядка, если оно рефлексивно,
антисимметрично и транзитивно. Отношение называется отношением строгого
порядка,
если оно антирефлексивно, антисимметрично и транзитивно.
Пр. а) отношение £ u ³ для чисел отношение нестрогого
б) отношение < u > для чисел отношение строгого
Лекция: Элементы общей алгебры
Р. Операции на множествах
Множество М вместе с заданной на нем совокупностью операций W = {j1
,., jm}, т.е. система А = {М1;j1,., jm
} называется алгеброй. W - сигнатура.
Если M1ÌM и если значения j( M1), т.е. замкнуто ==> A1={М1;j1,., jm} подалгебра A.
Пр. 1. Алгебра (R;+;*) – называется полем действительных чисел обе операции
бинарные и
поэтому тип этой алгебры (2;2)
- B=(Б;È;Ç) – булева алгебра. тип операций (2;2;1)
Р. Свойства бинарных алгебраических операций
запись ajb.
1. (ajb)jc=aj(bjc) – ассоциативная операция
Пр. +,x – сложение и умножения чисел ассоциативно
2. ajb = bja – коммутативная операция
Пр. +,x – коммутат.
–; : – некоммут.
умножение мат A×B ¹ B×A – некоммутативно.
3. aj(bjc) = (ajb) j(ajc) –дистрибутивность слева
(ajb)jc) = (ajс) j(bjc) –дистрибутивность справа.
Пр. (ab)e=aebe – возведение в степень
дистрибутивного отношения произведения справа
но не abc ¹ abac
Р. Гомоморфизм и изоморфизм
Алгебры с разными членами имеют различные строения. Алгебры с одинаковыми
членами имеют сходство. Пусть даны две алгебры A=(K; jI) и B=(M; j
I) – одинакового типа.
Пусть отображение Г:KàM при условии Г(jI)= jI
(Г), (1) т.е. результат не зависит от последовательности возможных операций: Или
сначала вып. операции jI b А и затем отображении Г, или сначала
отображение Г, или сначала отображение Г и затем отображение jI в В.
Тогда условие (1) называется Гомоморфизмом алгебры А в алгебру В.
Когда существует взаимооднозначный гомоморфизм его называют изоморфизмом. В
этом случае существует обратное отображение Г-1.
Мощности изоморфных алгебр равны.
Пр. Алгебры (QN; +) и (Q2; +) – отображение
типа и условие (1) запишется как 2(а+b)=2а+2b.
Отношение изоморфизма является отношением эквивалентности на множестве алгебр,
т.е вычисление рефлексивное, симметричности и транзитивности. Изоморфизм
важнейшее понятие в математике. Полученные соотношения в алгебре А
автоматически .. на изоморфные алгебры.
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



