|
|
| Лекция: Курс лекций по теории вероятностей |
Во втором случае пусть k0 = [np + p] (целая часть
числа np + p, то есть наибольшее целое число, не превосходящее np +
p). Из неравенств (a), (b) следует, что
Действительно, неравенство Р(vn = k0) > Р(vn
= k0+1), например, следует из (b), примененного для
k = k0+1 > np + p.
Видим, что в зависимости от того, является число 1 > np + p целым или
нет, имеется либо два равновероятных «наиболее вероятных» числа успехов k
0 = np + p и k0 –1 > np + p - 1,либо одно
«наиболее вероятное» число успехов k0 = [np + p].
Сформулируем уже доказанное утверждение в виде теоремы.
Теорема 12. В n испытаниях схемы Бернулли с вероятностью успеха
p наиболее вероятным числом успехов является
a) единственное число k0 = [np + p], если число np + p не целое;
б) два числа k0 = np + p и k0 -1= np + p -1, если число np + p целое.
Пример 19. Если p = q = 1/2, то при четном числе испытаний n
число np + p = n/2 + 1 /2— не целое, так что наиболее вероятным является
единственное число успехов [n/2 + 1 /2] = n/2. Что совершенно
понятно, так как есть нечетное число возможностей — получить 0, 1, .n
успехов, причем вероятности получить k и n-k успехов одинаковы.
При нечетном же числе испытаний n число np + p = n/2 + 1 /2 —
целое, так что наиболее вероятными (и одинаково вероятными) являются два числа
успехов n/2 + 1 /2 и n/2 - 1 /2.
5.3 Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха p в одном испытании.
Испытания проводятся до появления первого успеха. Введем величину τ
, равную номеру первого успешного испытания.
Теорема 13. Вероятность того, что первый успех произойдет в испытании с
номером k, равна
P(τ = k) = p qk-1.
Доказательство. Действительно,
Определение 21. Набор чисел {p qk-1 }
называется геометрическим распределением вероятностей и обозначается G
p или G(p).
Геометрическое распределение вероятностей обладает интересным свойством, которое
можно назвать свойством «нестарения». Пусть величина τ обозначает, скажем,
время безотказной работы (измеряемое целым числом часов) некоторого устройства.
Предположим, что для величины τ вероятность принять любое свое значение k
в точности равна pqk-1. Справедливо следующее
утверждение.
Теорема 14. Пусть P(τ = k) = p qk-1. Тогда для произвольных n, k ³ 0
P(τ > n+k\ τ > n) = P(τ > k)
Данному равенству можно придать следующее звучание: если известно, что
устройство проработало без отказов n часов, то вероятность ему работать еще не
менее k часов точно такая же, как вероятность проработать не менее k часов для
нового устройства.
Можно прочесть эту формулу и так: вероятность работающему устройству
проработать еще сколько-то часов не зависит от того момента, когда мы начали
отсчет времени, или от того, сколько уже работает устройство.
Доказательство. По определению условной вероятности,
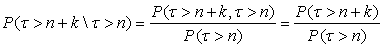 (4)
Последнее равенство следует из того, что событие {τ > n+k}
влечет событие {τ > n}, так что пересечение этих событий есть
{τ > n+k}. Найдем для произвольного m ³ 0 вероятность
P(τ > m).
Можно также заметить, что событие {τ > m} означает, что в схеме
Бернулли первые m испытаний завершились «неудачами», а это событие имеет
вероятность как раз qm.
Возвращаясь к (4), получим
5.4 Приближение гипергеометрического распределения биномиальным
Рассмотрим урну, содержащую N шаров, из которых K шаров — белые,
а оставшиеся N-K шаров — черные. Из урны наудачу (без возвращения)
выбираются n шаров. Вероятность PN,K
(n, k) того, что будет выбрано ровно k белых и n-k черных
шаров, находится по формуле (см. определение 8 гипергеометрического
распределения вероятностей):
Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров
почти не меняет пропорцию белых и черных шаров в урне, так что вероятности P
N,K(n, k) не очень отличаются от вероятностей в
процедуре выбора с возвращением
P(получить ровно k белых шаров при выборе n шаров с возвращением) =
Сформулируем нашу первую предельную теорему.
Теорема 15. Если N → ∞ и K → ∞
так, что K/N → p Î (0, 1) то для любых фиксированных n,
0<=k<=n (4)
Последнее равенство следует из того, что событие {τ > n+k}
влечет событие {τ > n}, так что пересечение этих событий есть
{τ > n+k}. Найдем для произвольного m ³ 0 вероятность
P(τ > m).
Можно также заметить, что событие {τ > m} означает, что в схеме
Бернулли первые m испытаний завершились «неудачами», а это событие имеет
вероятность как раз qm.
Возвращаясь к (4), получим
5.4 Приближение гипергеометрического распределения биномиальным
Рассмотрим урну, содержащую N шаров, из которых K шаров — белые,
а оставшиеся N-K шаров — черные. Из урны наудачу (без возвращения)
выбираются n шаров. Вероятность PN,K
(n, k) того, что будет выбрано ровно k белых и n-k черных
шаров, находится по формуле (см. определение 8 гипергеометрического
распределения вероятностей):
Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров
почти не меняет пропорцию белых и черных шаров в урне, так что вероятности P
N,K(n, k) не очень отличаются от вероятностей в
процедуре выбора с возвращением
P(получить ровно k белых шаров при выборе n шаров с возвращением) =
Сформулируем нашу первую предельную теорему.
Теорема 15. Если N → ∞ и K → ∞
так, что K/N → p Î (0, 1) то для любых фиксированных n,
0<=k<=n
5.5 Независимые испытания с несколькими исходами
Рассмотрим следующий пример, когда из двух очень похожих вопросов на один
можно ответить, пользуясь формулой Бернулли, а для другого этой формулы
оказывается недостаточно:
Пример 20. Игральная кость подбрасывается 15 раз. Найти вероятности
следующих событий:
а) выпадет ровно 10 шестерок; б) выпадет ровно 10 шестерок и три единицы.
а) есть 15 испытаний схемы Бернулли с вероятностью успеха 1/6 (выпадение
шестерки). Вероятность десяти успехов в 15 испытаниях равна
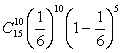 б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки,
выпадение единицы, выпадение остальных граней. Воспользоваться формулой для
числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.
Осталось изобрести формулу для подсчета вероятности каждому исходу в
нескольких независимых испытаниях выпасть нужное число раз, если в одном
испытании возможно не два, а более исходов.
Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, .m.
Пусть исход i в одном испытании случается с вероятностью рi, 1
≤ i ≤ m и
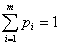 Обозначим через Р(n1,n2,.,nm) вероятность
того, что в n = n1+ n2+ .+nm независимых
испытаний исход 1 появился n1, раз, исход 2 – n2 раз,.
Теорема 16. Для любого n и любых целых n1
≥ 0. nm ≥ 0 таких, что n
1+ n2+ .+nm = n, верна формула:
Обозначим через Р(n1,n2,.,nm) вероятность
того, что в n = n1+ n2+ .+nm независимых
испытаний исход 1 появился n1, раз, исход 2 – n2 раз,.
Теорема 16. Для любого n и любых целых n1
≥ 0. nm ≥ 0 таких, что n
1+ n2+ .+nm = n, верна формула:
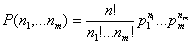 Доказательство. Рассмотрим один элементарный исход, благоприятствующий
выпадению n1 единиц, n2 двоек, . , n
m раз m-ок:
Доказательство. Рассмотрим один элементарный исход, благоприятствующий
выпадению n1 единиц, n2 двоек, . , n
m раз m-ок:
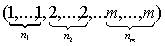 Это результат n экспериментов, когда все нужные исходы появились в
некотором заранее заданном порядке. Вероятность такого результата n
независимых испытаний равна
Это результат n экспериментов, когда все нужные исходы появились в
некотором заранее заданном порядке. Вероятность такого результата n
независимых испытаний равна
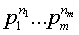 Все остальные благоприятные исходы отличаются лишь расположением чисел 1, 2,
.m на n местах. Число таких исходов равно числу способов расставить
на n местах n1 единиц, n2 двоек,
, . , nm раз чисел m, то есть
Все остальные благоприятные исходы отличаются лишь расположением чисел 1, 2,
.m на n местах. Число таких исходов равно числу способов расставить
на n местах n1 единиц, n2 двоек,
, . , nm раз чисел m, то есть
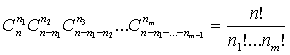 Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как
вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего
исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10
шестерок, 3 единицы и еще 2 других очка равна
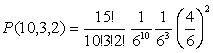
5.6 Теорема Пуассона для схемы Бернулли
Предположим, нам нужна вероятность получить не менее десяти успехов в 1000
испытаний схемы Бернулли с вероятностью успеха 0.003. Вероятность этого
события равна любому из следующих выражений:
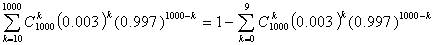 и вычисление даже одного слагаемого в каждом из этих выражений весьма
проблематично.
Сформулируем теорему о приближенном вычислении вероятности какого-либо числа
успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью
успеха. Термин «большое число» должен означать n → ∞. Если
при этом p = pn→ 0,то, очевидно, вероятность получить
любое конечное число успехов при растущем числе испытаний стремится к нулю.
Необходимо чтобы вероятность успеха p = pn→ 0
одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность
успеха меняться не может (см. определение схемы Бернулли).
Поэтому рассмотрим «схему серий»: есть
одно испытание ○ с вероятностью успеха p1
два испытания ○ , ○ с вероятностью успеха p2
.
n испытаний ○ , . , ○ с вероятностью успеха pn
.
Вероятность успеха меняется не внутри одной серии испытаний, а от серии к
серии, когда меняется общее число испытаний. Обозначим через vn
число успехов в n-той серии испытаний.
Теорема 17 (Теорема Пуассона).
Пусть n → ∞ , pn→ 0 так, что n
pn→ λ > 0. Тогда для любого k ≥
0 вероятность получить k успехов в n испытаниях схемы Бернулли с
вероятностью успеха pn стремится к величине
и вычисление даже одного слагаемого в каждом из этих выражений весьма
проблематично.
Сформулируем теорему о приближенном вычислении вероятности какого-либо числа
успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью
успеха. Термин «большое число» должен означать n → ∞. Если
при этом p = pn→ 0,то, очевидно, вероятность получить
любое конечное число успехов при растущем числе испытаний стремится к нулю.
Необходимо чтобы вероятность успеха p = pn→ 0
одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность
успеха меняться не может (см. определение схемы Бернулли).
Поэтому рассмотрим «схему серий»: есть
одно испытание ○ с вероятностью успеха p1
два испытания ○ , ○ с вероятностью успеха p2
.
n испытаний ○ , . , ○ с вероятностью успеха pn
.
Вероятность успеха меняется не внутри одной серии испытаний, а от серии к
серии, когда меняется общее число испытаний. Обозначим через vn
число успехов в n-той серии испытаний.
Теорема 17 (Теорема Пуассона).
Пусть n → ∞ , pn→ 0 так, что n
pn→ λ > 0. Тогда для любого k ≥
0 вероятность получить k успехов в n испытаниях схемы Бернулли с
вероятностью успеха pn стремится к величине
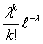 (5)
(5)
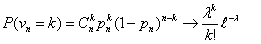 для n → ∞ , pn→ 0 так, что n pn→ λ
Определение 22. Пусть λ > 0— некоторая постоянная. Набор
чисел для n → ∞ , pn→ 0 так, что n pn→ λ
Определение 22. Пусть λ > 0— некоторая постоянная. Набор
чисел 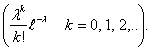 называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство называется
распределением Пуассона с параметром λ.
Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее
десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с
вычисления которой мы начали. Поскольку n = 1000 «велико», а p
n = 0.003 «мало», то, взяв λ = n pn = 3 ,
можно написать приближенное равенство
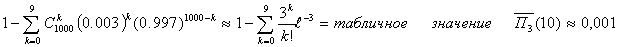 (6)
Осталось решить, а достаточно ли n=103 «велико», а p
n = 0.003 «мало», чтобы заменить точную вероятность P(vn
= k) на приближенное значение
(6)
Осталось решить, а достаточно ли n=103 «велико», а p
n = 0.003 «мало», чтобы заменить точную вероятность P(vn
= k) на приближенное значение
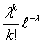 Для этого нужно уметь оценивать разницу между этими двумя вероятностями.
Теорема 18 (Теорема Пуассона с оценкой погрешности).
Пусть A Í {0, 1, ., n} — произвольное множество целых
неотрицательных чисел, vn — число успехов в n
испытаниях схемы Бернулли с вероятностью успеха p, λ = n p.
Тогда
Для этого нужно уметь оценивать разницу между этими двумя вероятностями.
Теорема 18 (Теорема Пуассона с оценкой погрешности).
Пусть A Í {0, 1, ., n} — произвольное множество целых
неотрицательных чисел, vn — число успехов в n
испытаниях схемы Бернулли с вероятностью успеха p, λ = n p.
Тогда
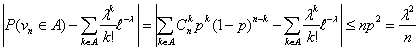 Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно
ли n «велико», а p «мало», руководствуясь полученной величиной
погрешности.
Какова же погрешность в формуле (6)?
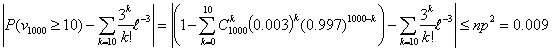 Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть
Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае,
можно утверждать, что искомая вероятность никак не больше, чем
0,01=0,001+0,009.
Рассмотрим еще одну формулу приближенного вычисления pn (m)
когда n велико. В отличии от предыдущего результата число успехов m в
этом случае тоже растет с ростом n, а вероятность успеха постоянна.
Локальная теорема Муавра – Лапласа
Пусть 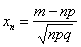 .Предположим, что .Предположим, что 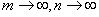 и величины и величины 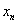 являются ограниченными. Тогда являются ограниченными. Тогда
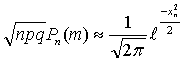 В частности, если
В частности, если 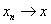 , то , то
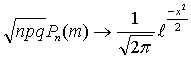 Доказательство:
В силу ограниченности величин
Доказательство:
В силу ограниченности величин 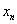 разность
разность 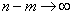 вместе с
n и m Воспользуемся формулой Стирлинга вместе с
n и m Воспользуемся формулой Стирлинга
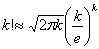
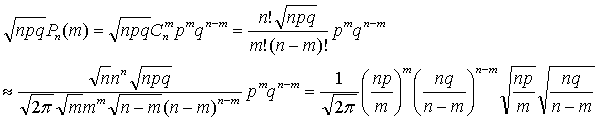 В силу определения
В силу определения 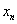
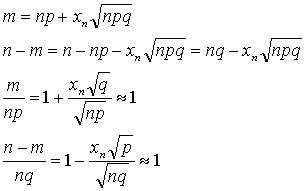
Раздел 6. Случайные величины и их распределения 6.1 Случайные величины
Мы уже видели, что для очень многих экспериментов нет никаких различий в
подсчете вероятностей событий, тогда как элементарные исходы в этих
экспериментах очень различаются. Но нас и должны интересовать именно
вероятности событий, а не структура пространства элементарных исходов. Поэтому
пора во всех таких «похожих» экспериментах вместо самых разных элементарных
исходов использовать, например, числа. То есть ввести соответствие (иначе
говоря, отображение) между элементарными исходами и вещественными числами (с
ними удобно работать).
Пусть имеется случайный эксперимент и задано вероятностное пространство
(Ω, Ψ,Р).
Определение 23. Функция ξ: Ω →R называется
случайной величиной, если для любого х Î R множество
{ ξ < x} = {ω: ξ(ω) < x} является событием, то
есть принадлежит σ-алгебре событий Ψ.
Замечание 10. Можно смело считать, что любое множество элементарных
исходов есть событие, и, следовательно, случайная величина есть
произвольная функция из Ω в R. Никаких неприятностей на
практике это обычно не влечет.
Определение 24. Будем говорить, что функция ξ: Ω →R
является Ψ -измеримой, если {ω: ξ(ω) < x}
принадлежит Ψ для любого х Î R.
Итак, случайная величина есть Ψ - измеримая функция, ставящая в
соответствие каждому элементарному исходу ω Î Ω число
ξ(ω) Î R.
Пример 21. Подбрасываем 1 раз кубик. Пусть Ω = {1, 2, 3, 4, 5,
6} , и две функции из Ω в заданы так: ξ(ω)=
ω , η(ω)= ω2.
Если Ψ есть множество всех подмножеств Ω, то
ξ и η являются случайными величинами, поскольку любое
множество элементарных исходов принадлежит Ψ, в том числе и {ω:
ξ(ω) < x} или {ω: η (ω) < x} .
Можно записать соответствие между значениями случайных величин ξ и
η вероятностями принимать эти значения в виде «таблицы распределения
вероятностей» или, коротко, «таблицы распределения»:
ξ | 1 | 2 | 3 | 4 | 5 | 6 | Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Страницы: 1, 2, 3
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



