|
|
| Лекция: Лекции по математической статистике |
Эти четыре момента составляют набор особенностей распределения при анализе
данных.
Нормальное распределение
Нормальное распределение лучше всего описывается кривой созданной ДеМуавром
по следующей формуле:
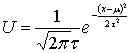 где U – высота кривой над осью x, t и μ – числа,
которые определяют положение кривой относительно числовой оси и регулируют ее
размах. Для μ=0, t=1 график принимает вид:
где U – высота кривой над осью x, t и μ – числа,
которые определяют положение кривой относительно числовой оси и регулируют ее
размах. Для μ=0, t=1 график принимает вид:
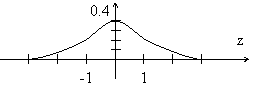 Эта кривая при
μ=0, t=1 получила статус стандарта, ее называют единичной
нормальной кривой, то есть любые собранные данные стремятся преобразовать
так, чтобы кривая их распределения была максимально близка к этой стандартной
кривой. Созданы статистические таблицы со значениями площади под единичной
нормальной кривой влево от любой точки на оси z в (-3; 3). Общая
площадь под кривой равна 1. И все остальные площади рассматривают как процент
от целого.
Свойства нормальных кривых:
Семейство нормальных кривых включают в себе все кривые, которые можно получить
по данной формуле, отличающиеся друг от друга только парой значений t и
μ .
1. 68% площади лежит в интервале Эта кривая при
μ=0, t=1 получила статус стандарта, ее называют единичной
нормальной кривой, то есть любые собранные данные стремятся преобразовать
так, чтобы кривая их распределения была максимально близка к этой стандартной
кривой. Созданы статистические таблицы со значениями площади под единичной
нормальной кривой влево от любой точки на оси z в (-3; 3). Общая
площадь под кривой равна 1. И все остальные площади рассматривают как процент
от целого.
Свойства нормальных кривых:
Семейство нормальных кривых включают в себе все кривые, которые можно получить
по данной формуле, отличающиеся друг от друга только парой значений t и
μ .
1. 68% площади лежит в интервале 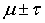 2. 95% площади лежит в интервале
2. 95% площади лежит в интервале 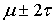 3. 99,7% площади лежит в интервале
3. 99,7% площади лежит в интервале 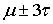 Если x имеет нормальное распределение со средним μ и
стандартным отклонение t, то z равное
Если x имеет нормальное распределение со средним μ и
стандартным отклонение t, то z равное 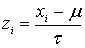 характеризуется распределением со средним равным нулю и стандартным отклонением
равным 1. Площадь между двумя значениями x в нормальном распределении
равна площади между ux стандартизованными величинами в единичном
нормальном распределении. Нормализованную кривую изобрели для решения задач
теории вероятности, но оказалось на практике, что она отлично аппроксимирует
распределение черт при большом числе наблюдений для множества переменных. Можно
предположить, сто не имея материальных ограничений на количество объектов и
время проведения эксперимента, статистическое исследование приводило к
нормально кривой.
Двумерное нормальное распределение
Если при исследовании появляется вопрос о связи между двумя переменными для
одного и того же объекта (например, рост и интеллект) мы говорим о двумерных
связях и результаты эксперимента находят свое отражение в двумерном
распределении частот.
Уравнение поверхности называется двумерным нормальным распределением (гладкая
непрерывная колоколообразная поверхность)
Характеристики нормального распределения
· Распределение значений x без учета значений y есть
нормальное распределение;
· Распределение значений y без учета значений x, тоже
нормальное распределение;
· Для каждого фиксированного значения x значение y дают
нормальное распределение с дисперсией
характеризуется распределением со средним равным нулю и стандартным отклонением
равным 1. Площадь между двумя значениями x в нормальном распределении
равна площади между ux стандартизованными величинами в единичном
нормальном распределении. Нормализованную кривую изобрели для решения задач
теории вероятности, но оказалось на практике, что она отлично аппроксимирует
распределение черт при большом числе наблюдений для множества переменных. Можно
предположить, сто не имея материальных ограничений на количество объектов и
время проведения эксперимента, статистическое исследование приводило к
нормально кривой.
Двумерное нормальное распределение
Если при исследовании появляется вопрос о связи между двумя переменными для
одного и того же объекта (например, рост и интеллект) мы говорим о двумерных
связях и результаты эксперимента находят свое отражение в двумерном
распределении частот.
Уравнение поверхности называется двумерным нормальным распределением (гладкая
непрерывная колоколообразная поверхность)
Характеристики нормального распределения
· Распределение значений x без учета значений y есть
нормальное распределение;
· Распределение значений y без учета значений x, тоже
нормальное распределение;
· Для каждого фиксированного значения x значение y дают
нормальное распределение с дисперсией 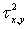 ;
· Для каждого фиксированного значения y значение x
распределяется нормально с дисперсией
;
· Для каждого фиксированного значения y значение x
распределяется нормально с дисперсией 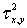 ;
· Среднее значения y для каждого отдельного значения x
ложатся на переменную.
Меры изменчивости
При решении вопроса о наличии взаимосвязи (корреляции) между двумя переменными,
руководствуются несколькими коэффициентами. Связь, выраженная графически,
называется диаграммной рассеивания, где x – оценка IQ, y
– оценка теста по математике.
Положение каждого объекта на диаграмме распределения определяется парой значений
xi, yi и выражаются по отношению к мере центральной
тенденции величинами
;
· Среднее значения y для каждого отдельного значения x
ложатся на переменную.
Меры изменчивости
При решении вопроса о наличии взаимосвязи (корреляции) между двумя переменными,
руководствуются несколькими коэффициентами. Связь, выраженная графически,
называется диаграммной рассеивания, где x – оценка IQ, y
– оценка теста по математике.
Положение каждого объекта на диаграмме распределения определяется парой значений
xi, yi и выражаются по отношению к мере центральной
тенденции величинами 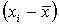 ,
, 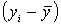 . Если объект
имеет высокие показатели по обеим переменным, то эти величины получаются
большими и положительными, в противном случае, если xi, yi
малы, то разность большой и отрицательной.
В дальнейшем будем говорить о произведении этих разностей и в том случае когда
наблюдается прямая связь между этими переменными, произведение будет большим и
положительным, следовательно такой же будет и сумма этих произведений . Если объект
имеет высокие показатели по обеим переменным, то эти величины получаются
большими и положительными, в противном случае, если xi, yi
малы, то разность большой и отрицательной.
В дальнейшем будем говорить о произведении этих разностей и в том случае когда
наблюдается прямая связь между этими переменными, произведение будет большим и
положительным, следовательно такой же будет и сумма этих произведений 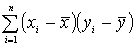 .
В случае обратной связи, когда большим значениям yi
соответствуют малые значения xi и наоборот, в этом случае
произведение разностей будет большим и отрицательным и сумма разностей также
будет большой и отрицательной.
Если между переменными не наблюдается какой-либо связи , количество
положительных и отрицательных произведений примерно рано и сумма их близка к
нулю. Таким образом большая положительная сумма – жесткая прямая зависимость;
большая отрицательная сумма – сильная обратная зависимость; близость к нулю –
отсутствие зависимости.
Недостатком этой меры является то, что ее величина зависит от числа пар
переменных x участвующих в расчетах.
Чтобы избежать связь независимого состояния V групп, мы усредняем эти значения:
.
В случае обратной связи, когда большим значениям yi
соответствуют малые значения xi и наоборот, в этом случае
произведение разностей будет большим и отрицательным и сумма разностей также
будет большой и отрицательной.
Если между переменными не наблюдается какой-либо связи , количество
положительных и отрицательных произведений примерно рано и сумма их близка к
нулю. Таким образом большая положительная сумма – жесткая прямая зависимость;
большая отрицательная сумма – сильная обратная зависимость; близость к нулю –
отсутствие зависимости.
Недостатком этой меры является то, что ее величина зависит от числа пар
переменных x участвующих в расчетах.
Чтобы избежать связь независимого состояния V групп, мы усредняем эти значения:
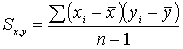 - ковариация
Частный случай, ковариация переменной с самой сабой – дисперсия
Чтобы избавить меру связи от отклонений двух групп значений: - ковариация
Частный случай, ковариация переменной с самой сабой – дисперсия
Чтобы избавить меру связи от отклонений двух групп значений:
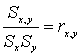 - коэффициент кореляции Пирсона или произведение моментов. - коэффициент кореляции Пирсона или произведение моментов.
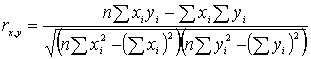 Значение коэффициента Пирсона не может выйти за границы интервала (-1; 1).
Влияние линейного преобразования переменных на коэффициент кореляции
Вместо xi вводим в формулу bx+ a, где a,
b – коэффициенты, для yi вводим в формулу dy+ c,
где c, d – коэффициенты.
Значение коэффициента Пирсона не может выйти за границы интервала (-1; 1).
Влияние линейного преобразования переменных на коэффициент кореляции
Вместо xi вводим в формулу bx+ a, где a,
b – коэффициенты, для yi вводим в формулу dy+ c,
где c, d – коэффициенты.
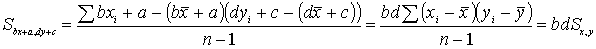
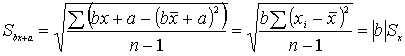
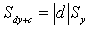
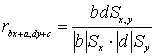 Вопрос о кореляции между переменными будучи решен положительно не означает
наличия более общего вида связи (заработная плата учителям и количество
поступивших в ВУЗы после окончания школы). Если мы проводим идентификацию
групп с различным средним, наличие кореляции не исключено, но возможно другое
объяснение взаимосвязи, чем вытекающее их эксперимента. Отсутствие связи при
нулевом коэффициента Пирсона означает всего лишь отсутствие линейной связи.
Дисперсия суммы и разности переменных
Вопрос о кореляции между переменными будучи решен положительно не означает
наличия более общего вида связи (заработная плата учителям и количество
поступивших в ВУЗы после окончания школы). Если мы проводим идентификацию
групп с различным средним, наличие кореляции не исключено, но возможно другое
объяснение взаимосвязи, чем вытекающее их эксперимента. Отсутствие связи при
нулевом коэффициента Пирсона означает всего лишь отсутствие линейной связи.
Дисперсия суммы и разности переменных
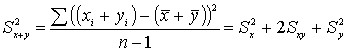
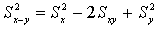
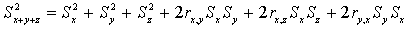 Предсказание и оценивание
Переменная, которую мы хотим оценить называется зависимой переменной или
откликом , обозначим ее через y.
Переменная которую мы используем для оценки называется независимой
переменной или фактором, ее обозначим через x.
Конкретная характеристика (переменная x) имеющаяся в нашем распоряжении,
позволяет получить до проведения эксперимента значение y, зависимой
переменной. Мы получаем
Предсказание и оценивание
Переменная, которую мы хотим оценить называется зависимой переменной или
откликом , обозначим ее через y.
Переменная которую мы используем для оценки называется независимой
переменной или фактором, ее обозначим через x.
Конкретная характеристика (переменная x) имеющаяся в нашем распоряжении,
позволяет получить до проведения эксперимента значение y, зависимой
переменной. Мы получаем 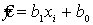 используя xi и коэффициенты b1 и b
0.
Даже при наилучшем линейном предсказании, предсказание
используя xi и коэффициенты b1 и b
0.
Даже при наилучшем линейном предсказании, предсказание 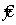 будет отличаться от реального yi на какую-то величину,
которую мы назовем ошибкой оценки и обозначим ei:
будет отличаться от реального yi на какую-то величину,
которую мы назовем ошибкой оценки и обозначим ei:
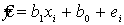 Точность предсказания зависит от того, насколько удачно подобраны коэффициента
b1 и b0. Критерием успешности подбора
коэффициентов является минимальная величина суммы квадратов всех ошибок оценки
Точность предсказания зависит от того, насколько удачно подобраны коэффициента
b1 и b0. Критерием успешности подбора
коэффициентов является минимальная величина суммы квадратов всех ошибок оценки 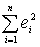 – критерий наименьших квадратов
Другой критерий:
– критерий наименьших квадратов
Другой критерий: 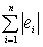 .
Этот критерий приводит к медианой линии регрессии. Из уравнения .
Этот критерий приводит к медианой линии регрессии. Из уравнения 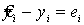 следует
следует 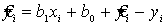 Исходя из минимизации формулы наименьших квадратов найдем формулы:
Исходя из минимизации формулы наименьших квадратов найдем формулы:
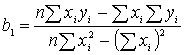 ; ; 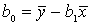 Наше исследование получается наиболее результативным, если мы предполагаем,
что фактор и отклик имеют двумерные нормальные распределения.
Свойства двумерного нормального распределения
1. Выборочные средние отклика (y) для каждого значения x лежат на прямой;
2. Для любого значения x, соответствующие значения y нормально распределены;
3. Для любого значения x, y – имеют одинаковую дисперсию
Наше исследование получается наиболее результативным, если мы предполагаем,
что фактор и отклик имеют двумерные нормальные распределения.
Свойства двумерного нормального распределения
1. Выборочные средние отклика (y) для каждого значения x лежат на прямой;
2. Для любого значения x, соответствующие значения y нормально распределены;
3. Для любого значения x, y – имеют одинаковую дисперсию 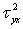 .
При прогнозировании является ли среднее ошибок оценки подходящей мерой для
прогнозирования. .
При прогнозировании является ли среднее ошибок оценки подходящей мерой для
прогнозирования.
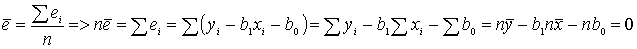 Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт,
это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.
Стандартная ошибка оценки
Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт,
это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.
Стандартная ошибка оценки 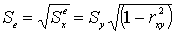 Стандартную ошибку оценки применяют для определения пределов, в окрестности
предсказанного
Стандартную ошибку оценки применяют для определения пределов, в окрестности
предсказанного  попадает фактическое значение yi.
В приделах Se – расположено 69% фактических значений объекта,
в приделах 2Se – 95%, в приделах 3Se –
97,5%.
Связь b1 и b0 с другими описательными статистиками
попадает фактическое значение yi.
В приделах Se – расположено 69% фактических значений объекта,
в приделах 2Se – 95%, в приделах 3Se –
97,5%.
Связь b1 и b0 с другими описательными статистиками
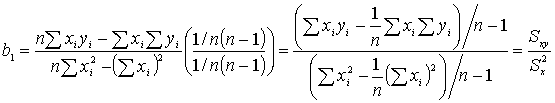
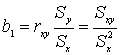 Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то
Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то 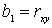 .
Поскольку rxy не зависит от Sx и S
y, b1 - принимает максимальное значение при r
xy =1 и минимальное значение при rxy = -1,
следовательно b1 никогда не может быть больше .
Поскольку rxy не зависит от Sx и S
y, b1 - принимает максимальное значение при r
xy =1 и минимальное значение при rxy = -1,
следовательно b1 никогда не может быть больше 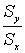 , при rxy =1 и не может быть меньше
, при rxy =1 и не может быть меньше 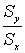 при rxy = -1.
Если между переменными отсутствует линейная связь, b1=0
уравнение регрессии сводится к прямой без наклона, то есть
при rxy = -1.
Если между переменными отсутствует линейная связь, b1=0
уравнение регрессии сводится к прямой без наклона, то есть 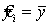 .
Измерение нелинейной связи между переменными
Для определения меры нелинейной связи между переменными используется коэффициент
.
Измерение нелинейной связи между переменными
Для определения меры нелинейной связи между переменными используется коэффициент 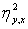
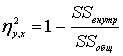 Эта мера может быть использована и для оценки линейной связи.
Пример вычисления:
Эта мера может быть использована и для оценки линейной связи.
Пример вычисления:
| x/возраст | 10 | 14 | 18 | 22 | 26 | 30 | 34 | 38 | | 7 | 8 | 9 | 11 | 9 | 8 | 7 | 8 | | 8 | 9 | 10 | 11 | 10 | 9 | 9 | | | 9 | 10 | 11 | 12 | 11 | 9 | 10 | | | 9 | 11 | 12 | 12 | | 10 | | | | 10 | | | | | | | |
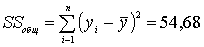 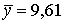 Находим среднее для каждого возраста и суммируем отношения каждого yi
от среднего соответствующего группы.
Для 10 -
Находим среднее для каждого возраста и суммируем отношения каждого yi
от среднего соответствующего группы.
Для 10 - 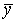 =8,6; 18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8. =8,6; 18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.
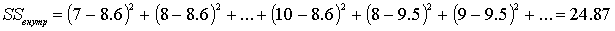
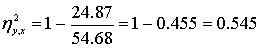
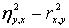 - является мерой нелинейности связи и - является мерой нелинейности связи и 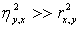 Другие меры связи
1. Измерения в дихотомической шкале (например, женат – не женат, мужчина
– женщина)
2. Измерение в дихотомической шкале наименований в предположении
нормального распределения. Предполагается, что при более полных, более
совершенных измерениях данные распределятся по нормальному закону.
3. Шкала порядка
4. Измерение в шкале интервалов или отношений.
Другие меры связи
1. Измерения в дихотомической шкале (например, женат – не женат, мужчина
– женщина)
2. Измерение в дихотомической шкале наименований в предположении
нормального распределения. Предполагается, что при более полных, более
совершенных измерениях данные распределятся по нормальному закону.
3. Шкала порядка
4. Измерение в шкале интервалов или отношений.
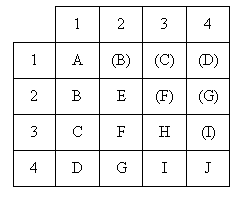 Рассмотренный ранее коэффициент кореляции Пирсона соответствует сочетанию J при
измерении исходных данных. Для описания степени кореляции при других
комбинациях шкал измерений исходных данных используются следующие меры.
Случай A.
Рассмотренный ранее коэффициент кореляции Пирсона соответствует сочетанию J при
измерении исходных данных. Для описания степени кореляции при других
комбинациях шкал измерений исходных данных используются следующие меры.
Случай A.
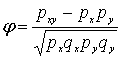 px – доля людей имеющих 1 по x, py – доля людей имеющих 1 по y
qx – доля людей имеющих 0 по x, qy – доля людей имеющих 0 по y
pxy - доля людей имеющих 1 по x и y
px – доля людей имеющих 1 по x, py – доля людей имеющих 1 по y
qx – доля людей имеющих 0 по x, qy – доля людей имеющих 0 по y
pxy - доля людей имеющих 1 по x и y
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | | x | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | | y | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
x – женат / холост
y – исключенные из учебного заведения / оставшиеся
px =0,4167 ; py = 0,5 ; qx =0,5833 ; qy = 0,5 ; pxy =0,333; φ=0,507
Если нет особого интереса к доле px и py, дихатомические
данные располагают в таблице сопряженности признаков. Пример таблицы
сопряженности по приведенным данным
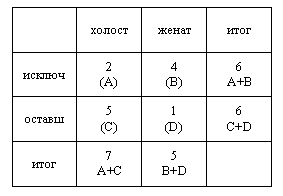 φ – определяется по формуле: φ – определяется по формуле:
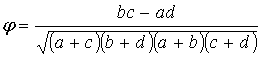 Коэффициент φ, это тот же коэффициент кореляции Пирсона, но эти данные
не похожи на двумерное нормальное распределение, которое мы представляли при
вычислении коэффициента Пирсона. Это рассматривается как большое неудобство
статистиками.
Случай B.
Удовлетворительного коэффициента для этого случая не существует,
рекомендуется исходить из предположения о нормальном распределении данных и
вычислять φ в качестве меры связи для этого случая.
Случай C.
Для этого случая подходят коэффициенты, о котором мы расскажем в случае I.
Случай D.
Используется биссериальный коэффициент кореляции:
Коэффициент φ, это тот же коэффициент кореляции Пирсона, но эти данные
не похожи на двумерное нормальное распределение, которое мы представляли при
вычислении коэффициента Пирсона. Это рассматривается как большое неудобство
статистиками.
Случай B.
Удовлетворительного коэффициента для этого случая не существует,
рекомендуется исходить из предположения о нормальном распределении данных и
вычислять φ в качестве меры связи для этого случая.
Случай C.
Для этого случая подходят коэффициенты, о котором мы расскажем в случае I.
Случай D.
Используется биссериальный коэффициент кореляции: 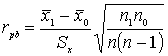
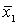 - среднее по x объектов имеющих 1 по y. - среднее по x объектов имеющих 1 по y.
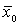 - среднее по x объектов имеющих 0 по y.
Sx – стандартное отклонение
Случай E.
Тетрахорический коэффициент кореляции: - среднее по x объектов имеющих 0 по y.
Sx – стандартное отклонение
Случай E.
Тетрахорический коэффициент кореляции: 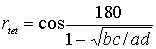 Более удобно при расчете обращаться к статическим таблицам, содержащим
вычисления из этого уравнения. Они составлены при условии, что bc/ad>1
. В противном случае таблица содержит ad/bc и величина тетрахорического
коэффициента будет отрицательной.
Случай F.
Удовлетворительного коэффициента не разработано, рекомендуется продположить
нормальное распределение для x и использовать биссериальный ранговый
коэффициент (см. случай G).
Случай G.
Биссериальный коэффициент:
Более удобно при расчете обращаться к статическим таблицам, содержащим
вычисления из этого уравнения. Они составлены при условии, что bc/ad>1
. В противном случае таблица содержит ad/bc и величина тетрахорического
коэффициента будет отрицательной.
Случай F.
Удовлетворительного коэффициента не разработано, рекомендуется продположить
нормальное распределение для x и использовать биссериальный ранговый
коэффициент (см. случай G).
Случай G.
Биссериальный коэффициент: 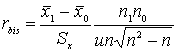 u – ордината нормального распределения.
Случай H.
Используется коэффициент ранговой кореляции Спирмана:
u – ордината нормального распределения.
Случай H.
Используется коэффициент ранговой кореляции Спирмана: 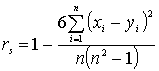 В том случае, если при измерении встречается связанные ранги, это уравнение
не подходит в качестве меры кореляции.
Связанный ранг возникает в том случае, если у некоторых объектов получено
одинаковое значение переменной. В этом случае ранги, которые должны были бы
получить эти объекты суммируются и делятся на количество объектов и каждый
получает, пролученный при вычислении ранг.
До сих пор коэффициенты кореляции представляли из себя или могли быть
объяснены в терминах произведения моментов. Коэффициент кореляции, не
связвнный с моментами построен Кендаллом и называется τ – Кендалла
В том случае, если при измерении встречается связанные ранги, это уравнение
не подходит в качестве меры кореляции.
Связанный ранг возникает в том случае, если у некоторых объектов получено
одинаковое значение переменной. В этом случае ранги, которые должны были бы
получить эти объекты суммируются и делятся на количество объектов и каждый
получает, пролученный при вычислении ранг.
До сих пор коэффициенты кореляции представляли из себя или могли быть
объяснены в терминах произведения моментов. Коэффициент кореляции, не
связвнный с моментами построен Кендаллом и называется τ – Кендалла
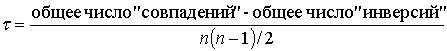 Случай I.
Для этого случая коэффициенты не разработаны, рекомендуется преобразовать оценки
по y в ранги и найти или коэффициент Спирмана или Кендалла
Бисериальная ранговая кореляция:
Случай I.
Для этого случая коэффициенты не разработаны, рекомендуется преобразовать оценки
по y в ранги и найти или коэффициент Спирмана или Кендалла
Бисериальная ранговая кореляция: 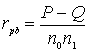 P – сумма всех совпадений; Q – сумма всех инверсий;
n0 – число объектов при нулевой дихотомии; n1
– число объектов при единичной дихотомии.
P – сумма всех совпадений; Q – сумма всех инверсий;
n0 – число объектов при нулевой дихотомии; n1
– число объектов при единичной дихотомии.
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



