|
|
| Лекция: Математическая Логика |
Правило одновременной подстановки.
Замечание: Если формула 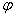 выводима, то выводима и выводима, то выводима и 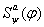 Возьмем формативную последовательность вывода
Возьмем формативную последовательность вывода  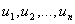 и добавим в неё
и добавим в неё 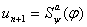 ,
получившаяся последовательность является формальным выводом.
(Если выводима ,
получившаяся последовательность является формальным выводом.
(Если выводима 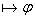 то если то если 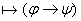 , то выводима , то выводима 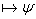 )
Теор: Если выводимая формула )
Теор: Если выводимая формула 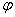 , то , то 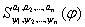 ( (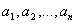 - различные символы переменных) выводима
Выберем - различные символы переменных) выводима
Выберем 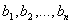 - символы
переменных которые различны между собой и не входят не в одну из формул - символы
переменных которые различны между собой и не входят не в одну из формул 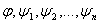 , сделаем подстановку
, сделаем подстановку 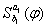 и последовательно применим
и последовательно применим 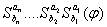 и в новом слове делаем последовательную подстановку:
и в новом слове делаем последовательную подстановку: 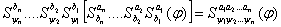 , где
, где 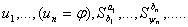 - является
формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез - является
формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез 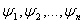 (формулы), называется такая последовательность слов
(формулы), называется такая последовательность слов 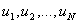 , каждая из которых удовлетворяет условию:
, каждая из которых удовлетворяет условию:
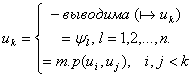
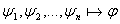 если формулу если формулу 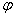 можно включить в некоторый формальный вывод из гипотез можно включить в некоторый формальный вывод из гипотез 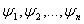 .
Лемма: .
Лемма: 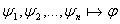 ; ; 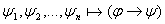 : то тогда : то тогда 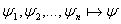 Напишем список:
Напишем список:
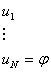 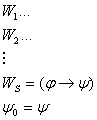 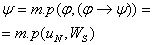 Лемма:
Лемма:
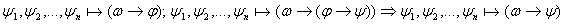 Док:
Док: 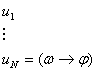 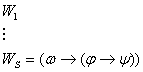 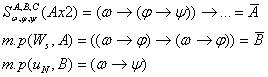 3.1.4 Теорема Дедукции.
Если из
3.1.4 Теорема Дедукции.
Если из
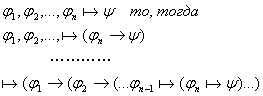 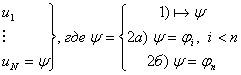 1) и 2а)
1) и 2а) 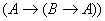 , где , где 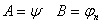 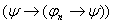 по правилу m.p. по правилу m.p. 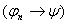 , ч.т.д.
2б) , ч.т.д.
2б) 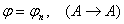 - уже выводили - уже выводили 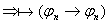 , ч.т.д.
Базис индукции: N=1 , ч.т.д.
Базис индукции: N=1 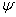 - формальный вывод из длинного списка - формальный вывод из длинного списка 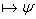
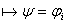 (только что доказано), осуществим переход по индукции: (только что доказано), осуществим переход по индукции:
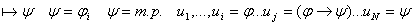
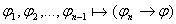 по индукции по индукции
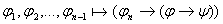 и по лемме 2 и по лемме 2
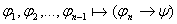 Пример:
Пример: 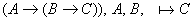
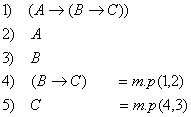 по теореме дедукции по теореме дедукции 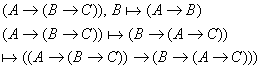 3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
3.2 Критерий выводимости в ИВ.
3.2.1 Формулировка теоремы.
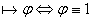 - тавтология
при любой интерпретации алфавита (символов переменных) - тавтология
при любой интерпретации алфавита (символов переменных)
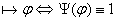 3.2.2 Понятие интерпретации.
3.2.2 Понятие интерпретации.
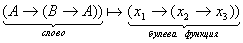 символ переменной
символ переменной 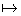 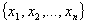 переменную поставим в соответствие. переменную поставим в соответствие.
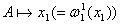 , где , где 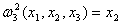 - проекция на - проекция на 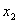 . .
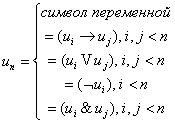 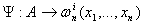
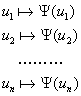 ; ; 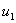 - только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где: - только символ
переменных, т.к.
это заглавное слово
формативной последо-
вательности вида:
Где:
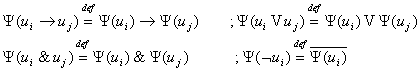 3.2.3 Доказательство теоремы.
3.2.3 Доказательство теоремы.
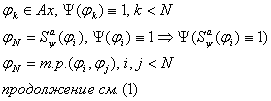 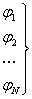
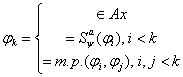 формальный
вывод формальный
вывод 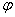
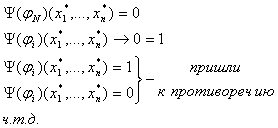 (1)
(1) 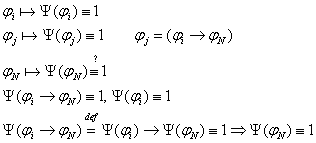 3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем.
3.3 Непротиворечивость ИВ.
3.3.1 Определение.
1) ИВ противоречиво, если формула А выводима в нем. 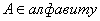 .
2) .
2) 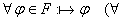 формула выводима в ИВ) формула выводима в ИВ)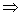 ИВ противоречиво.
3) ИВ противоречиво.
3) 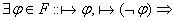 ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к
любому из трех определений.
Док-во: (1) Если ИВ противоречиво.
ИВ непротиворечиво, если оно не является противоречивым.
Теорема: ИВ является непротиворечивым исчислением по отношению к
любому из трех определений.
Док-во: (1) Если 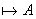 , то соответствующая ей булева функция будет тождественно равна 1.
, то соответствующая ей булева функция будет тождественно равна 1.
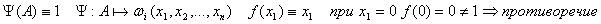 (2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3) Пусть
(2) Если любая формула выводима, то выводима и А, что соответствует пункту 1.
(3) Пусть 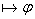 и и 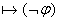 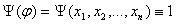 - булева функция - булева функция
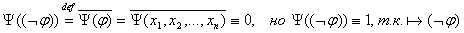 - противоречие.
3.4 Формальные исчисления.
Алфавит – конечное или счетное множество символов, возможно,
разбитых на группы. Алфавит должен быть упорядоченным множеством.
Слово – конечная упорядоченная последовательность символов
алфавита, в т.ч. пустое слово.
V – множество всех слов.
Вычислимая функция от нескольких натуральных переменных
- противоречие.
3.4 Формальные исчисления.
Алфавит – конечное или счетное множество символов, возможно,
разбитых на группы. Алфавит должен быть упорядоченным множеством.
Слово – конечная упорядоченная последовательность символов
алфавита, в т.ч. пустое слово.
V – множество всех слов.
Вычислимая функция от нескольких натуральных переменных 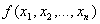 ( f – может быть не всюду определенной )
f – называется вычислимой, если
( f – может быть не всюду определенной )
f – называется вычислимой, если 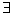 такая машина Тьюринга, которая её вычисляет. такая машина Тьюринга, которая её вычисляет.
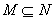 - разрешимое множество, если характеристическая функция - разрешимое множество, если характеристическая функция
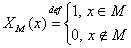 - является вычислимой.
Множество - является вычислимой.
Множество 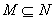 называется перечислимым, если называется перечислимым, если 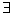 такая вычислимая функция такая вычислимая функция
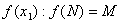 М - разрешимо
М - разрешимо 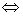 М и N \M перечислимы.
М – перечислимо М и N \M перечислимы.
М – перечислимо 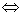 М – область определения некоторой вычислимой функции.
Множество всех формул F – некоторое разрешимое подмножество V.
Т – счетное множество, если М – область определения некоторой вычислимой функции.
Множество всех формул F – некоторое разрешимое подмножество V.
Т – счетное множество, если 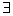 его биективное отображение на V. его биективное отображение на V.
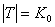 - обозначение счетного множества. ( - обозначение счетного множества. (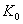 - алеф-нуль)
Если - алеф-нуль)
Если 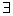 и зафиксировано биективное и вычислимое отображение и зафиксировано биективное и вычислимое отображение 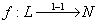 (вычис.),
то L – ансамбль.
V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение: В произвольном формальном исчислении: (вычис.),
то L – ансамбль.
V – ансамбль (слова лексикографически упорядочены и занумерованы)
Определение: В произвольном формальном исчислении: 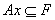 - множество всех аксиом – разрешимое подмножество множества всех формул.
- множество всех аксиом – разрешимое подмножество множества всех формул.
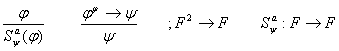 Правило вывода:
Правило вывода:
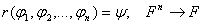 ,при ,при 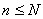 разрешимо. Для ИВ N=2.
Пример: разрешимо. Для ИВ N=2.
Пример:
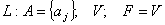 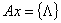 (пустое слово) , (пустое слово) , 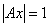
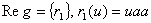
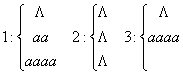 1 и 2 – формальные выводы.
3 – не является формальным выводом. 1 и 2 – формальные выводы.
3 – не является формальным выводом.
4 Предикаты и кванторы.
4.1 Определение предиката.
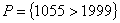
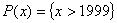 - высказывание, содержащее переменную. - высказывание, содержащее переменную.
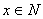 - предметная область предиката. - предметная область предиката.
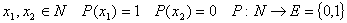 Пусть А – множество объектов произвольной природы (предметная область
предиката).
Пусть А – множество объектов произвольной природы (предметная область
предиката).
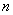 -местный предикат – произвольное отображение -местный предикат – произвольное отображение 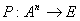 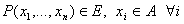
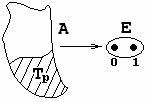 Множество истинности данного предиката Множество истинности данного предиката 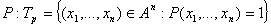
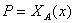 -
- характеристическая
функция от x на множестве
А - совпадает
с предикатами -
- характеристическая
функция от x на множестве
А - совпадает
с предикатами
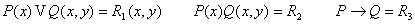

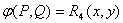 4.2 Понятие квантора.
4.2 Понятие квантора.
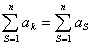 k – связанная переменная
n – свободная переменная k – связанная переменная
n – свободная переменная
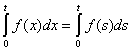 t – свободная, x – связанная. t – свободная, x – связанная.
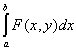 , a,b,y – свободные переменные, x – связанная. , a,b,y – свободные переменные, x – связанная.
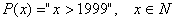
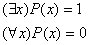
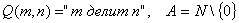
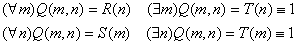 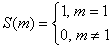
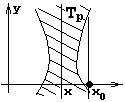
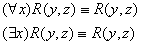 4.3 Геометрическая интерпретация навешивания кванторов.
4.3 Геометрическая интерпретация навешивания кванторов.
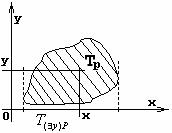
| 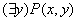
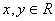
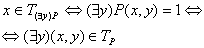 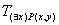 - ортогональная проекция на ось x - ортогональная проекция на ось x
| 
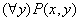
|
Пронесение отрицания через кванторы
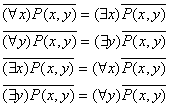 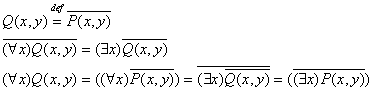 Геометрическое 'доказательство':
Геометрическое 'доказательство':
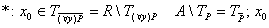 не обладает свойством, что прямая не обладает свойством, что прямая 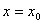 целиком лежит в целиком лежит в 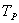
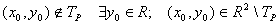
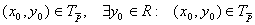
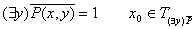 ч.т.д. ч.т.д.
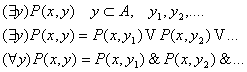
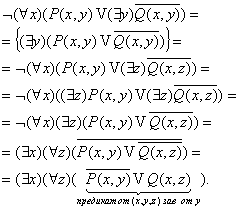
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



