Каталог Рефератов - Реферат: Алгебраическая проблема собственных значений

	Информационно-образоательный портал
	Рефераты, курсовые, дипломы, научные работы,



МЕНЮ\|

поиск

Реферат: Алгебраическая проблема собственных значений

	*	*	0	0	0
	*	*	*	*	*
A1=	0	*	*	*	*	после первого основного шага,
	0	*	*	*	*	состоящего из трех преобразований,
	0	*	*	*	*

	*	*	0	0	0
	*	*	*	0	0
A2=	0	*	*	*	*	после второго основного шага,
	0	0	*	*	*	состоящего из двух преобразований,
	0	0	*	*	*

	*	*	0	0	0
	*	*	*	0	0	после третьего основного шага,
A3=	0	*	*	*	0	состоящего из одного преобразования.
	0	0	*	*	*	Теперь матрица имеет трехдиагональный вид.
	0	0	0	*	*

На каждом основном шаге изменяются лишь те элементы матрицы аij, которые расположены в ее правой нижней (заштрихованной) части. Таким образом на k-м шаге преобразуется только матрица порядка (п — k + 1), занимающая правый нижний угол исходной матрицы. Ясно, что на каждой следующей стадии выполняется меньшее число преобразований, чем на предыдущей. Всего для приведения матрицы к трехдиагональному виду требуется выполнить (n 2 — Зп + 2)/2 преобразований. Наш опыт применения метода Гивенса показывает, что можно при выполнении одного шага преобразований обратить в нуль сразу все элементы целой строки и столбца, стоящие вне трех диагоналей матрицы. Метод, позволяющий выполнить такое преобразование, предложил Хаусхолдер . Метод Хаусхолдера для симметричных матриц Метод Хаусхолдера позволяет привести матрицу к трехдиагональному виду, выполнив почти вдвое меньше вычислений по сравнению с другими методами. Это обусловлено тем, что при его применении становятся нулевыми сразу все элементы строк и столбцов, стоящие вне трех диагоналей матрицы. Метод Хаусхолдера позволяет получить требуемый результат быстрее, чем метод Гивенса, так как связан с выполнением меньшего числа, хотя и более сложных преобразований. Это его свойство особенно ярко проявляется применительно к большим матрицам. Хотя в методе Хаусхолдера вместо плоских вращении используются эрмитовы ортогональные преобразования матриц, трехдиагональная форма матрицы, которую получают этим методом, имеет те же собственные значения, что и трехдиагональная матрица, получаемая методом Гивенса. При использовании метода Хаусхолдера на п — 2 основных шагах выполняются следующие преобразования: Аk = РkAk-1Рk, k=1, 2, ..., п-2, где Aо == А. Каждая преобразующая матрица имеет вид uk ukT Pk = E - -------------- , 2Kk2 где ui,k = 0 при i = 1, 2, ., k, ui,k = ak,i при i = k+2, ., n, uk+1,k = ak,k+1 ± Sk. Здесь n 1/2 Sk = S a2k,i i=k+1 2K2k = S2k ± ak, k+1 Sk. В этих уравнениях берется знак, соответствующий элементу ak, k+1. Это позволяет сделать значение иk+1,k максимальным. Отметим, что методами Гивенса и Хаусхолдера можно пользоваться и в случае несимметричных матриц, приводя их, правда, не к трехдиагональному, а другому частному виду треугольной матрицы известной как матрица Гессенберга:

*	*	0	0	0	0
*	*	*	0	0	0
*	*	*	*	0	0
*	*	*	*	*	0
*	*	*	*	*	*
*	*	*	*	*	*

5. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ СИММЕТРИЧНОЙ ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЫ Приведя симметричную матрицу к трехдиагональному виду методом Гивенса или Хаусхолдера, необходимо найти ее собственные значения. Чтобы ясней были достоинства трехдиагональной формы, сформулируем задачу о собственных значениях в виде dеt(А—lE) = 0, где А — симметричная трехдиагональная матрица. Раcкрыв выражение в скобках, получим

a1 - l	b2		0
b1	a2 - l			= 0
			bn	= 0
0		bn	an - l

Произвольный определитель порядка п можно выразить через п миноров порядка п — 1, каждый из которых в свою очередь выражается через п — 1 миноров порядка п — 2. Удобство трехдиагональной формы в том, что на каждом шаге все миноры, кроме двух, оказываются равными нулю. В результате исходный определитель представляется последовательностью полиномов fm(l) = (am - l) fm-1 (l) – b2 m fm-2(l). Приняв f0 (l) = 1 и f1 (l) = a1 - l при r = 2, .... п, получим совокупность полиномов, известную как последовательность Штурма и обладающую тем свойством, что корни полинома fj (l) располагаются между корнями полинома fj+1 (l). Поэтому для f 1 (l) = a1— l можно утверждать, что значение lК = а 1 заключено между корнями полинома f2 (l) == (a2 — l) (a1 — l) —b22. Это облегчает итерационное определение корней полинома, так как если известны границы интервалов, в которых лежат значения корней полинома, то их можно найти методом половинного деления. Так последовательно находят корни всех полиномов, и последний из них fn (l) дает все искомые п собственные значения. Эту процедуру можно проиллюстрировать графически (см. рис. 3). Последовательность Штурма обладает еще и таким свойством: для любого значения b, при котором fn (b) <> 0, число собственных значений матрицы A, больших b, равно числу изменений знака последовательности 1, f1 (b), f2 (b), . , (1)n fn (b). Если целое число, равное числу изменений знака, обозначить через V(b), то число собственных значений в интервале действительных чисел [b, с] будет равно V(b)—V(c).

Корень многочлена

f1 (l)

f1 (b)

Реферат: Алгебраическая проблема собственных значений

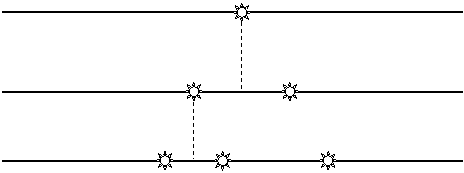
Корни многочлена

f2 (l)

f1 (b)

Корни многочлена

f3 (l)

f1 (b)

.........................................

Корни многочлена

fn-1 (l)

f1 (b)

Реферат: Алгебраическая проблема собственных значений

Корни многочлена

fn (l)

f1 (b)

Рис. 3. Итерационное определение корней полинома 6. ДРУГИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ В этом разделе мы рассмотрим два метода определения собственных значений, имеющие большое практическое значение. Оба разработаны в последние 20 лет и наиболее эффективны в тех случаях, когда требуется найти все собственные значения произвольной матрицы действительных или комплексных чисел. В обоих используются преобразования, позволяющие получить последовательность подобных матриц, сходящуюся к матрице блочной треугольной формы:

X1	*		.	.	*	*	*
	x2	*	.	.	*	*	*
		x3	.	.	*	*	*
			.	.	*	*	*
				.	*	*	*
					.	*	*
	0					.	*
							*

где блоки Хm, представляют собой матрицы размерности 2 х 2, расположенные на главной диагонали. Собственные значения блоков Хm , являются в то же время собственными значениями исходной матрицы размерности п x п. Такая форма удобна, так как детерминант второго порядка блоков Х m позволяет определять комплексные собственные значения, не вводя комплексных элементов в окончательную матрицу. Если все собственные значения исходной матрицы действительные, то в окончательном виде она будет треугольной, причем собственные значения будут расположены на диагонали. Метод LR Этот метод первоначально был разработан Рутисхаузером в 1958 г. Метод основан на представлении матрицы A в виде произведения А = LR, где L — левая треугольная матрица с единичными диагональными элементами, а R — правая треугольная. Применяя преобразование подобия L-1 A R, видим, что, A2 = L-1 A R = L-1 (RL)L = R L. Следовательно, Am-1 = L m-1 Rm-1, Am = R m-1 Lm-1. Этот процесс повторяется до тех пор, пока Ls не превратится в единичную матрицу Е, а Rs не приобретет квазидиагональную форму. Хотя этот метод очень удобен, он не всегда устойчив. Поэтому предпочтение часто отдают другому методу. Метод QR Метод QR. предложен Фрэнсисом в 1961 г. Соответствующий ему алгоритм определяется соотношением Am = Q m Rm. где Q m — ортогональная матрица, а Rm — верхняя треугольная матрица. При использовании метода последовательно получаем Am+1 = Q mT Am Q m = Q mT Q m Rm Q m = Rm Q m. В пределе последовательность матриц А стремится к квазидиагональной форме. Этот метод сложнее предыдущего и требует больших затрат машинного времени. Однако его устойчивость,обусловленная использованием ортогональных преобразующих матриц, обеспечила ему прочную репутацию лучшего метода решения задач самой общей формы. Пример 3 Пусть требуется найти все собственные значения произвольной матрицы размерности 6 x 6

2,3	4,3	5,6	3,2	1,4	2,2
1,4	2,4	5,7	8,4	3,4	5,2
2,5	6,5	4,2	7,1	4,7	9,3
3,8	5,7	2,9	1,6	2,5	7,9
2,4	5,4	3,7	6,2	3,9	1,8
1,8	1,7	3,9	4,6	5,7	5,9

Сделаем это в два приема, приведя сначала матрицу с помощью преобразования подобия к виду Гсссенберга, затем с помощью разновидности метода QR найдем собственные значения. В приведенной ниже программе использованы две подпрограммы из пакета программ для научных исследований фирмы IВМ. Подпрограмма НSВС преобразует матрицу размерности 6 x 6 к форме Гессенберга, а подпрограмма АТЕIG позволяет найти собственные значения. {**********************************************************************} Программа определение всех собственных значений произвольной матрицы размерности 6х5. Используются подпрограммы НSВС и АТЕIG из пакета программ для научных исследований фирмы IBM {**********************************************************************} DIMENSION A(6,6),RR(6),RI(6),IANA(6) READ(5,100)((A(I,J),J=1,6),I=1,6) WRITE(6,104) 104 FORMAT(///lX,’THE ORIGINAL MATRIX IS AS FOLLOWS’) WRITE(6,103) 103 FORMAT(1X,65(-'--')) WRITE(6,101)((A(I,J),J=1,6),I=1,6) WRITE(6,103) 101FORMAT(6(1X,F10.5)) 100 FORMAT(6F10.5) CALL HSBG(6,A,6) WRITE(6,105) 105 FORMAT(///1X,'THE MATRIX W HESSENBUR5 FORM IS') WRITE(6,103) WRITE(6,101)((A(I,J),J=1,6),I=1,6) WRITE(6,103) CALL ATEIG(6,A,RR,RI,IANA,6) WRITE(6,106) 106FORHAT(///1X,'THE EIGENVALUES ARE AS FOLLOUS') WRITE(6,107) 107 FORMAT (1X, 23(‘-‘),/,4X,’REAL',12X,’IMAG’,/,23(‘-‘)) WRITE(6,102)(RR(I),PKI),I=1,6) WRITE(6,108) 108 FORMAT(1X,23(‘-‘)) FORMAT<2(2X,F10.5)» STOP END

Результат получаем в виде

Исходная матрица имеет вид

2.30000	4.30000	5.60000	3.20000	1,40000	2.20000
1.40000	2.40000	5.70000	8.40000	3.40000	5.20000
2.50000	6.50000	4.20000	7.10000	4.70000	9.30000
3.80000	5.70000	2.90000	1.60000	2.50000	7.90000
2.40000	5.40000	3.70000	6.20000	3.90000	1.80000
1.80000	1.70000	3.90000	4.60000	5.70000	5.90000

Матрица в форме Гессенберга.

-1.13162	3.20402 -0,	-0.05631	3.88246	1.40000	2.20000
-0.75823	0.07468 0,	0.48742	6.97388	5.37А35	10.36283
0.	1.13783 -2,	-2.63803	10.18618	7.15297	17.06242
0.	0.	3.35891	7. 50550	7.09754	13.92154
0.	0.	0.	13.36279	10.58947	16.78421
0.	0.	0.	0.	5.70000	5.90000

Собственные значения ----------------------------------- Действит. Миним. -----------------------------------

25.52757	0.
-5.63130	0.
0.88433	3.44455
0.88433	-3.44455
-0.68247	1.56596
-0.68247	-1.56596

7. ВЫБОР АЛГОРИТМА РЕШЕНИЯ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ Выбор подходящего алгоритма для решения той или иной задачи на собственные значения определяется типом собственных значений, типом матрицы и числом искомых собственных значений. Чем сложнее задача, тем меньше число алгоритмов, из которых можно выбирать. Таблица 1 позволяет облегчить этот выбор. Обычно пакеты математического обеспечения ЭВМ содержат подпрограммы, в которых используются все эти алгоритмы или некоторые из них. Одним из эффективных способов использования имеющегося математического обеспечения является одновременное применение двух подпрограмм, позволяющее совместить их лучшие качества. Например, имея матрицу общего вида, можно методом Хаусхолдера свести ее к виду Гессенберга, а затем с помощью алгоритма QR найти собственные значения. При этом будут использованы как быстрота, обеспечиваемая методом Хаусхолдера, так и универсальность алгоритма QR. Таблица 1 Выбор алгоритма решения задачи на собственные значения

Название алгоритма	Применяется для	Результат	Рекомендуется для отыскания собственных значений			Примечание


			Наибольшего или наименьшего	Всех <=6	Всех >=6
Определитель (итерация)	Матриц общего вида	Собственные значения		*		Требует нахождения корней полинома общего вида
Итерация (итерация)	То же	Собственные значения и собственные векторы	*	*	*	Обеспечивает наилучшую точность для наибольшего и наименьшего собственных значений
Метод Якоби (преобразование)	Симметричных матриц	Диагональная форма матрицы		*	*	Теоретически требует бесконечного числа шагов
Метод Гивенса (преобразование)	То же	Трехдииональльная форма матрицы		*	*	Требует знания корней простого полинома
Метод Гивенса (преобразование)	Несимметричных матриц	Форма Гессенберга		*	*	Требует применения дополнительного метода
Метод Хаусхолдера (преобразование)	Симметричных матриц	Трехдиагональная форма матрицы		*	*	Требует знания корней простого полинома
Метод Хаусхолдера (преобразование)	Несимметричных матриц	Форма Гессенберга		*	*	Требует применения дополнительного метода
Метод LR (преобразование)	Матриц общего вида	Квазидиагональная форма матрицы		*	*	Бывает неустойчив
Метод QR (преобразование)	То же	То же		*	*	Лучший метод, обладающий наибольшей общностью

Страницы: 1, 2, 3

© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент.

Корень многочлена

Корни многочлена

Корни многочлена

Корни многочлена

Корни многочлена

Результат получаем в виде

Рекомендуется для

Примечание