|
|
| Реферат: Оптимальные решения |
В ячейках E11:H11 суммируем количество досок и деталей.
Вводим формулы:
G11 - ABS(2*F11-G11)
G12 - ABS(G11-2*H11)
G13 - ABS(F11-H11)
Входим во встроенную функцию EXCEL Поиск Решения
Устанавливаем Целевую ячейку E11
Ставим ограничения:
E3:E10=>0
E3:E10= ЦЕЛЫЕ
G12<=1
G13<=1
G14<=1
Даем команду Выполнить
Машина выдает разультаты
| Способы | 3м | 2м | 1,5м | Количество | 3м | 2м | 1,5м | 1 | 2 | 0 | 1 | 34 | 68 | 0 | 34 | 2 | 0 | 3 | 1 | 33 | 0 | 99 | 33 | 3 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 4 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 5 | 1 | 2 | 0 | 47 | 47 | 94 | 0 | 6 | 0 | 2 | 2 | 24 | 0 | 48 | 48 | 7 | 1 | 1 | 1 | 12 | 12 | 12 | 12 | 8 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | | | | | 150 | 127 | 253 | 127 | | | | | | | 1 | | | | | | | | 1 | | | | | | | | | |
Видно, что для полных 127 комплектов не хватает одной двухметровой детали.
То есть максимальное число комплектов – 126. Остаток – по одной детали всех
типов.
Ответ: максимальное число комплектов – 126
3. Использование свойств квадратичной функции при решении экстремальных задач
Задача 5.
Окно имеет форму прямоугольника ,завершенного полукругом. Периметр фигуры
равен 6м .Каковы должны быть размеры окна,чтобы окно пропускало наибольшее
количество света?
Решение.
Окно будет обладать наибольшей пропускной способностью,если при заданном
периметре будет иметь максимальную площадь.
Пусть AB=x, AD=y,тогда
P=AB+BC+AD+ DMC
P=x+2y+0,5 p x (1)
S=AB*BC+p x /8
S=xy+ x p/8 (2)
Из (1),(2) следует, что
S(x)=-(p/8 +1/2)x +3x
Известно,что квадратный трехчлен принимает наибольшее значение при
x =-b/2a,т.е. x =12/(p +4), y= 6/ (p +4).
Ответ.Размеры окна 6/(p +4),12/(p +4).
Задача 6.
На учебном полигоне произведен выстрел из зенитного орудия в вертикальном
направлении не разрывающимся снарядом. Требуется определить наибольшую высоту
подъема снаряда, если начальная скорость снаряда ν0 = 300 м/с.
Сопротивлением воздуха
пренебречь.
Решение.
Из курса физики известно, что путь s, пройденный телом при равноускоренном
движении, изменяется в зависимости от времени по закону s = s0 +
ν0 t + at2/ 2, где s0 – начальный путь,
ν0 – начальная скорость, a – ускорение, t – время.
В рассматриваемом случае s =0,v =300 м/с, а=-5 м/с ,значит,S(t) = 300t –
5t2 .
Функция S(t) принимает наибольшее значение при
S(30)= 300*30-5*302 =4500(м)
Наибольшая высота подъема снаряда равна 4500 м.
Как видно из примеров, решение экстремальных задач дает возможность установить
более тесную межпредметную связь алгебры, геометрии и физики. При их решении
можно приобрести не только математическую информацию, но и знания из курса
физики.
Решение физических задач поучительно с точки зрения математики, так как можно
Показать тонкости тех или иных математических приемов в действии, в их
практическом
приложении.
В частности, эти задачи помогают осознать, что функция, заданная аналитической
формулой, может выражать зависимости между реальными величинами в самых
различных явлениях и процессах
Задача 7.
Арка моста имеет форму параболы (высота 4 м, наибольшая ширина 20 м).
Составьте уравнение этой параболы.
Решение.
Уравнение параболы в данном случае имеет вид y = ax2 + c. Для определения a и c
подставим в этом уравнение координаты точек B и C (рис. 1), т.е.
4 = c c = 4
c = 4,
Þ Þ
0 = 100a + c 100a = -4
a = - 0,04
Парабола имеет вид: y = - 0,04x2 + 4.
 у
у
 х
4.Применение методов дифференциального исчисления при решении прикладных задач.
х
4.Применение методов дифференциального исчисления при решении прикладных задач.
Задача 8.
Проектируется канал оросительной системы с прямоугольным сечением в 4,5 м2
. Каковы должны быть размеры сечения, чтобы для облицовки стенок и дна пошло
наименьшее количество материала?
Решение.
Пусть стенки канала имеют длину x м., а дно канала – y м.
Тогда:
 x*y=4,5 y=4,5/x
S= L*(2x+y) S=L*(2x+4,5/x)
Найдем производную. x*y=4,5 y=4,5/x
S= L*(2x+y) S=L*(2x+4,5/x)
Найдем производную.
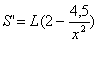 Так как S’=0, и L(длина канала)-положительное число,то Так как S’=0, и L(длина канала)-положительное число,то
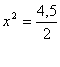 x=1,5
Легко убедиться, что при данном x значение S минимально
Ответ: x=1,5 м. y=3 м.
Задача 9.
.
Какова должна быть скорость парохода,чтобы общая сумма расходов на один км.
пути была наименьшей, если расходы на топливо за один час пропорциональна
квадрату скорости.
Решение.
Расходы на 1км пути на эксплуатацию парохода состоят из расходов на топливо и
других расходов (содержание команды, амортизация). Ясно, что чем быстрее
движется пароход, тем больше расход топлива. Остальные расходы от скорости
движения не зависят.
Обозначим через S-сумму расходов в час
V- скорость судна
Расходы на 1км выразится формулой S/V
По условию имеем S=KV2+b, где
K- коэффициент пропорциональности,
b- расходы, кроме расходов на топливо.
Y=S/V Y=(KV2+b)/V=KV+b/V
Надо найти значение V, при котором функция Y=KV+b/V имеет наименьшее значение.
Y¢=K=b/V2 Y¢=0
V=Öb/V
Таким образом общая сумма расходов на 1 км. пути будет наименьшей при
V=Öb/V.
Значение коэффициентов b и K определяются из опыта эксплуатации парохода.
Задача 10.
Над центром круглого стола радиусом r висит лампа. На какой высоте h следует
повесить эту лампу, чтобы на краях стола получить наибольшую освещенность?
Из физики известна формула E=k*sinj/(h2+r2)
sinj=h/Ö(h2+r2)
Для упрощения решения задачи вместо функции
E=k*sinj/(h2+r2)=k*h/(h2+r2)3/2 возьмем функцию
T=1/k2*E2=h2/(h2+r2), для упрощения формулы заменим
h2=z
тогда:
T=z/(z+r2)3 T¢= ((z+r2)3-z*3*(z+r2)2)/ (z+r2)6=
=(z+r2-3*r)/ ((z+r2)4
T¢=0® r2-2*r=0® z=r2/2 h=r/Ö2
Ответ. Освещенность максимальная, если h=r/Ö2
Задача 11.
Нахождение гидравлически наиболее выгодного трапециидального сечения русла.
Из всех сечений русла, представляющих собою равнобедренную трапецию, имеющих
одинаковую площадь w и уклон i, найти то, которое будет пропускать
наибольший расход Q.
Пояснение:
1. Расход Q –это количество воды, проходящее через поперечное сечение русла в
единицу времени
2. Расход Q определяется по формуле: Q=w*cÖr*j
w-площадьсечения
c-коэффициент
r-гидравлический радиус
i-уклон дна русла
3. Гидравлический радиус есть отношение площади сечения к смоченному
периметру c: r=w/c
4. Смоченный периметр есть линия соприкосновения жидкости с поверхностью канала.
5. Крутизна 1/m откоса есть отношение высоты откоса к заложению (АО).
Решение. Расход Q зависит от r, и он будет наибольшим при rmax , что
будет тогда, когдаcmin
Крутизна откоса 1/m =h/АО, то АО=h*m
Тогда w=1/2*(b+2*m*h+b)h=(b+m*h)*h
c=b+2*hÖ1+m2т.е.
c=(w/h-m*h)+2*hÖ1+m2
c(h)=(- w/h2-m)+2Ö1+m2
c(h)=-(b+m*h)/h-m+2Ö1+m2
c(h)=-b/h+2(Ö(1+m2)-m) c(h)=0 при b/h=2(Ö(1+m2)-m)
c(h)¢¢>0 при h=b/2(Ö(1+m2)-m)
Ответ.c имеет наименьшее значение при условии h=b/2(Ö(1+m2)-m)
Задача 12.
Рама из швеллера размера а * в перекрыта рифленой сталью, в которой вырезан круг
диаметром d с центром пересечения диагоналей прямоугольника. Для усиления
жесткости перекрытия решено окантовать круг уголками, устанавливаемыми под
Ð 45° к сторонам рамы и являющимися касательными к кругу.
Найти длину касательных.
Введем систему координат как
показано на рисунке.
D2D1 – касательная
Напишем уравнение касательной.
Для чего, зная ее угол наклона 45°
найдем точки касания.
Для этого продифференцируем
уравнение окружности
х2 + у2 = r2
х + у * у = 0
т.к. у¢ = 1 (у = tg 45°=1), то
у = -х.
r Ö 2 r Ö 2
Т.е. т. Е имеет координаты Е (- ¾¾ ; ¾¾ )
2 2
Cоставим уравнение D2D1: т.к. D2D1 ║ прямой у = х, то она имеет вид
rÖ 2
у = х +2 * ¾¾ => у = х + rÖ 2
2
Напишем уравнения АВ и ВС
А
АВ: х = - ¾
2
в
ВС: у = ¾
2
Найдем координаты т. Р2 решая систему
а а
y = х + r Ö 2 х = - ¾, у = - ¾ + r Ö 2
í а => 2 2
х = - ¾ a а
2 D2 ( - ¾; -
¾ + r Ö 2)
2 2
Найдем координаты т. D1
b b
y = х + r Ö 2 x = ¾ - r Ö 2,
у = ¾
í b 2 2
y = ¾ b b
2 D1 (
¾ - r Ö 2; ¾ )
2 2
Найдем D1D2
B a b a b a
D2D1 = Ö (¾ - r Ö 2 + ¾)2
+ (¾ + ¾ - r Ö 2)2 = Ö 2 * (¾ +
¾ - r Ö 2)
2 2 2 2 2 2
Ответ.Длина касательных
(a +b) Ö 2
D2D1 = ¾¾¾¾ - d .
2
Задача 13.
Найти наименьшую длину стрелы крана,
необходимую для монтажа плит перекры –
тия здания высотою Н, шириною а, при
условии, что кран может двигаться вдоль
фасада здания, параллельно ему.
Высота основания стрелы крана над землей
h1.
Зазор между стеной здания и стрелой крана должен быть всегда не менее m
Пояснение
1. На чертеже указан боковой фасад здания.
2. Кран должен подавать так, чтобы крюк его приходился точно над
серединой здания.
3. Длина стрелы крана, начало которой есть точка А1, а проекция
конца (крюка) точка М, меняется с изменением угла α.
Решение.
h2
1. Из ∆ АВD АВ= ¾¾
sin a
а
¾
2. Из ∆ ВСМ ВС = 2
¾¾
cos α
h2 а
3. т.е. Ð=АС=АВ+ВС , то l = ¾¾¾ +
¾¾¾ (3)
sin a 2cos a
т.к. величины h2 и a - постоянные, изучим функцию
a и l - переменные
h2 * cos a a * sin a
f¢'(a) = - ¾¾¾¾¾
+ ¾¾¾¾
sin2 a 2 cos2 a
l' (a) = 0
h2 cos a a * sin a
¾¾¾¾ = ¾¾¾¾
sin2 a 2 cos2 a
2 h2 2 h2
tg3 a = ¾¾ tg a = 3Ö ¾¾
a a
2. Найдем вторую производную
h2 (1+ cos2 a) a (1+ sin2 a)
l" (a) = ¾¾¾¾¾¾ +
¾¾¾¾¾
sin3 a 2 * cos3 a
т.к. a - острый, то
l" (a) > 0, значит при a из равенства
2h2 l'' (a) > 0, т.е. при этом значении a функция имеет минимум
tg a = 3Ö ¾¾ h2 = H + m – h1
a
2 (H + m – h1)
tg a = 3Ö ¾¾¾¾¾¾
a[11]
Ответ. при угле a , таком, что
2 (H + m – h1)
tg a = 3Ö ¾¾¾¾¾¾
a[12]
длина стрелы крана минимальна.
Таким образом, для решения задач оптимизации нужно выполнить следующие действия:
1) Выразить оптимизируемую величину как функцию некоторой переменной и
найти область определения этой функции.
2) Найти точки экстремума этой функции.
3) Вычислить значения функции в экстремальных точках и на концах
промежутка, где определяется функция
4) Выбрать из этих значений оптимальное.
Заключение.
В настоящее время получило всеобщее признание то, что успех развития многих
областей науки и техники существенно зависит от развития многих направлений
математики. Математика становится средством решения проблем организации
производства, поисков оптимальных решений и, в конечном счете, содействует
повышению производительности труда и устойчивому поступательному развитию
народного хозяйства.
Использование экстремальных задач при изучении математики оправдано тем,
что они с достаточной полнотой закладывают понимание того, как человек ищет,
постоянно добивается решения жизненных задач, чтобы получающиеся
результаты его деятельности были как можно лучше. Решая задачи указанного
типа, наблюдаем, с одной стороны, абстрактный характер математических
понятий, а с другой – большую эффективную их применимость к решению
жизненных практических задач.
Экстремальные задачи помогают ознакомиться с некоторыми идеями и
прикладными методами школьного курса математики, которые часто
применяются в трудовой деятельности, в познании окружающей
действительности.
Решение экстремальных задач способствует углублению и обогащению наших
математических знаний. Через задачи мы знакомимся с экстремальными
свойствами изучаемых функций, с некоторыми свойствами неравенств. Эти
задачи могут серьезно повлиять на содержание учебного материала, на аспекты
применения положений изучаемой теории на практике. x=1,5
Легко убедиться, что при данном x значение S минимально
Ответ: x=1,5 м. y=3 м.
Задача 9.
.
Какова должна быть скорость парохода,чтобы общая сумма расходов на один км.
пути была наименьшей, если расходы на топливо за один час пропорциональна
квадрату скорости.
Решение.
Расходы на 1км пути на эксплуатацию парохода состоят из расходов на топливо и
других расходов (содержание команды, амортизация). Ясно, что чем быстрее
движется пароход, тем больше расход топлива. Остальные расходы от скорости
движения не зависят.
Обозначим через S-сумму расходов в час
V- скорость судна
Расходы на 1км выразится формулой S/V
По условию имеем S=KV2+b, где
K- коэффициент пропорциональности,
b- расходы, кроме расходов на топливо.
Y=S/V Y=(KV2+b)/V=KV+b/V
Надо найти значение V, при котором функция Y=KV+b/V имеет наименьшее значение.
Y¢=K=b/V2 Y¢=0
V=Öb/V
Таким образом общая сумма расходов на 1 км. пути будет наименьшей при
V=Öb/V.
Значение коэффициентов b и K определяются из опыта эксплуатации парохода.
Задача 10.
Над центром круглого стола радиусом r висит лампа. На какой высоте h следует
повесить эту лампу, чтобы на краях стола получить наибольшую освещенность?
Из физики известна формула E=k*sinj/(h2+r2)
sinj=h/Ö(h2+r2)
Для упрощения решения задачи вместо функции
E=k*sinj/(h2+r2)=k*h/(h2+r2)3/2 возьмем функцию
T=1/k2*E2=h2/(h2+r2), для упрощения формулы заменим
h2=z
тогда:
T=z/(z+r2)3 T¢= ((z+r2)3-z*3*(z+r2)2)/ (z+r2)6=
=(z+r2-3*r)/ ((z+r2)4
T¢=0® r2-2*r=0® z=r2/2 h=r/Ö2
Ответ. Освещенность максимальная, если h=r/Ö2
Задача 11.
Нахождение гидравлически наиболее выгодного трапециидального сечения русла.
Из всех сечений русла, представляющих собою равнобедренную трапецию, имеющих
одинаковую площадь w и уклон i, найти то, которое будет пропускать
наибольший расход Q.
Пояснение:
1. Расход Q –это количество воды, проходящее через поперечное сечение русла в
единицу времени
2. Расход Q определяется по формуле: Q=w*cÖr*j
w-площадьсечения
c-коэффициент
r-гидравлический радиус
i-уклон дна русла
3. Гидравлический радиус есть отношение площади сечения к смоченному
периметру c: r=w/c
4. Смоченный периметр есть линия соприкосновения жидкости с поверхностью канала.
5. Крутизна 1/m откоса есть отношение высоты откоса к заложению (АО).
Решение. Расход Q зависит от r, и он будет наибольшим при rmax , что
будет тогда, когдаcmin
Крутизна откоса 1/m =h/АО, то АО=h*m
Тогда w=1/2*(b+2*m*h+b)h=(b+m*h)*h
c=b+2*hÖ1+m2т.е.
c=(w/h-m*h)+2*hÖ1+m2
c(h)=(- w/h2-m)+2Ö1+m2
c(h)=-(b+m*h)/h-m+2Ö1+m2
c(h)=-b/h+2(Ö(1+m2)-m) c(h)=0 при b/h=2(Ö(1+m2)-m)
c(h)¢¢>0 при h=b/2(Ö(1+m2)-m)
Ответ.c имеет наименьшее значение при условии h=b/2(Ö(1+m2)-m)
Задача 12.
Рама из швеллера размера а * в перекрыта рифленой сталью, в которой вырезан круг
диаметром d с центром пересечения диагоналей прямоугольника. Для усиления
жесткости перекрытия решено окантовать круг уголками, устанавливаемыми под
Ð 45° к сторонам рамы и являющимися касательными к кругу.
Найти длину касательных.
Введем систему координат как
показано на рисунке.
D2D1 – касательная
Напишем уравнение касательной.
Для чего, зная ее угол наклона 45°
найдем точки касания.
Для этого продифференцируем
уравнение окружности
х2 + у2 = r2
х + у * у = 0
т.к. у¢ = 1 (у = tg 45°=1), то
у = -х.
r Ö 2 r Ö 2
Т.е. т. Е имеет координаты Е (- ¾¾ ; ¾¾ )
2 2
Cоставим уравнение D2D1: т.к. D2D1 ║ прямой у = х, то она имеет вид
rÖ 2
у = х +2 * ¾¾ => у = х + rÖ 2
2
Напишем уравнения АВ и ВС
А
АВ: х = - ¾
2
в
ВС: у = ¾
2
Найдем координаты т. Р2 решая систему
а а
y = х + r Ö 2 х = - ¾, у = - ¾ + r Ö 2
í а => 2 2
х = - ¾ a а
2 D2 ( - ¾; -
¾ + r Ö 2)
2 2
Найдем координаты т. D1
b b
y = х + r Ö 2 x = ¾ - r Ö 2,
у = ¾
í b 2 2
y = ¾ b b
2 D1 (
¾ - r Ö 2; ¾ )
2 2
Найдем D1D2
B a b a b a
D2D1 = Ö (¾ - r Ö 2 + ¾)2
+ (¾ + ¾ - r Ö 2)2 = Ö 2 * (¾ +
¾ - r Ö 2)
2 2 2 2 2 2
Ответ.Длина касательных
(a +b) Ö 2
D2D1 = ¾¾¾¾ - d .
2
Задача 13.
Найти наименьшую длину стрелы крана,
необходимую для монтажа плит перекры –
тия здания высотою Н, шириною а, при
условии, что кран может двигаться вдоль
фасада здания, параллельно ему.
Высота основания стрелы крана над землей
h1.
Зазор между стеной здания и стрелой крана должен быть всегда не менее m
Пояснение
1. На чертеже указан боковой фасад здания.
2. Кран должен подавать так, чтобы крюк его приходился точно над
серединой здания.
3. Длина стрелы крана, начало которой есть точка А1, а проекция
конца (крюка) точка М, меняется с изменением угла α.
Решение.
h2
1. Из ∆ АВD АВ= ¾¾
sin a
а
¾
2. Из ∆ ВСМ ВС = 2
¾¾
cos α
h2 а
3. т.е. Ð=АС=АВ+ВС , то l = ¾¾¾ +
¾¾¾ (3)
sin a 2cos a
т.к. величины h2 и a - постоянные, изучим функцию
a и l - переменные
h2 * cos a a * sin a
f¢'(a) = - ¾¾¾¾¾
+ ¾¾¾¾
sin2 a 2 cos2 a
l' (a) = 0
h2 cos a a * sin a
¾¾¾¾ = ¾¾¾¾
sin2 a 2 cos2 a
2 h2 2 h2
tg3 a = ¾¾ tg a = 3Ö ¾¾
a a
2. Найдем вторую производную
h2 (1+ cos2 a) a (1+ sin2 a)
l" (a) = ¾¾¾¾¾¾ +
¾¾¾¾¾
sin3 a 2 * cos3 a
т.к. a - острый, то
l" (a) > 0, значит при a из равенства
2h2 l'' (a) > 0, т.е. при этом значении a функция имеет минимум
tg a = 3Ö ¾¾ h2 = H + m – h1
a
2 (H + m – h1)
tg a = 3Ö ¾¾¾¾¾¾
a[11]
Ответ. при угле a , таком, что
2 (H + m – h1)
tg a = 3Ö ¾¾¾¾¾¾
a[12]
длина стрелы крана минимальна.
Таким образом, для решения задач оптимизации нужно выполнить следующие действия:
1) Выразить оптимизируемую величину как функцию некоторой переменной и
найти область определения этой функции.
2) Найти точки экстремума этой функции.
3) Вычислить значения функции в экстремальных точках и на концах
промежутка, где определяется функция
4) Выбрать из этих значений оптимальное.
Заключение.
В настоящее время получило всеобщее признание то, что успех развития многих
областей науки и техники существенно зависит от развития многих направлений
математики. Математика становится средством решения проблем организации
производства, поисков оптимальных решений и, в конечном счете, содействует
повышению производительности труда и устойчивому поступательному развитию
народного хозяйства.
Использование экстремальных задач при изучении математики оправдано тем,
что они с достаточной полнотой закладывают понимание того, как человек ищет,
постоянно добивается решения жизненных задач, чтобы получающиеся
результаты его деятельности были как можно лучше. Решая задачи указанного
типа, наблюдаем, с одной стороны, абстрактный характер математических
понятий, а с другой – большую эффективную их применимость к решению
жизненных практических задач.
Экстремальные задачи помогают ознакомиться с некоторыми идеями и
прикладными методами школьного курса математики, которые часто
применяются в трудовой деятельности, в познании окружающей
действительности.
Решение экстремальных задач способствует углублению и обогащению наших
математических знаний. Через задачи мы знакомимся с экстремальными
свойствами изучаемых функций, с некоторыми свойствами неравенств. Эти
задачи могут серьезно повлиять на содержание учебного материала, на аспекты
применения положений изучаемой теории на практике.
Список литературы
1. Башмаков М. И. Алгебра и начала анализа 10-11. М.: Просвещение, 1992.
2. Беляева Э. С., Монахов В.М. Экстремальные задачи. М.: Просвещение, 1997.
3. Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение, 1978
4. Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.:
Просвещение, 1985.
5. Гейн А. Г. Земля Информатика. – Екатеринбург: Издательство Уральского
университета, 1997
6. Гнеденко Б. В. Введение в специальность математика. – М: Наука, 1991
7. Гнеденко Б. В. Математика в современном мире. М: Просвещение, 1980.
8. Перельман Я. И. Занимательная алгебра. М: АО «Столетие», 1994
9. Хургин Я. И. Ну и что? (Разговоры математика с биологами и радистами,
врачами и технологами. о математике и ее связях с другими науками). М.:
Молодая гвардия, 1967.
10. Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. – М.:
Просвещение, 1997
[11]
[12]
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



