|
|
| Реферат: Приложения производной |
На рисунке 6 изображена функция f (x), не имеющая в точке x0
производной [f' (x0) = ¥] и достигающая в этой точке
максимума. При x ® x0 и x < x0
f' (x) ® +¥, при x ® x0 и x >
x0 f' (x) ® -¥. Значит касательная кривой y = f (x)
при x = x0 перпендикулярна к оси Ox. Такие
точки называются точками возврата кривой y=f(x).
Таким образом, необходимым признаком существования в точке x0
экстремума функции f (x) является выполнение следующего условия: в точке x0
производная f' (x) или равна нулю, или не существует.
Этот признак не является достаточным условием существования экстремума функции
f (x) в точке x0 : можно привести много примеров функций,
удовлетворяющих этому условию при x = x0 , но, однако, не
достигающих экстремума при x = x0.
Например, производная функции y = x3 при x0 =
0 равна нулю, однако эта функция при x0 = 0 не достигает
экстремального значения.
6.2.Достаточные условия убывания и возрастания функции. Достаточные условия
экстремума функции.
Теорема 4.Если функция f(x) имеет в каждой точке интервала (a, b)
неотрицательную производную, то она является неубывающей функцией в этом
интервале.
Теорема 5. Если функция f(x) в каждой точке интервала (a, b) имеет
неположительную производную, то она является невозрастающей функцией в этом
интервале.
Теорема 6. (первый достаточный признак экстремума). Если производная
f '(x) функции f(x) обращается в нуль в точке x0 или не существует и
при переходе через x0 меняет свой знак, то функция f(x) имеет в этой
точке экстремум (максимум, если знак меняется с "+" на "-", и минимум, если
знак меняется с "-" на "+").
Теорема 7. (второй достаточный признак существования экстремума функции).
Если в точке x0 первая производная f '(x) функции f(x) обращается в
нуль, а её вторая производная f ''(x) отлична от нуля, то в точке x0
функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума,
если f ''(x) < 0). Предполагается, что f ''(x) непрерывна в точке x0
и ее окрестности.
6.3 .Правило нахождения экстремума
1°. Чтобы найти экстремум функции, надо:
1) найти производную данной функции;
2) приравнять производную нулю и решить полученное уравнение; из
полученных корней отобрать действительные и расположить их (для удобства) по их
величине от меньшего к большему; в том случае, когда все корни оказываются
мнимыми, данная функция не имеет экстремума;
3) определить знак производной в каждом из промежутков, отграниченных
стационарными точками ( стационарными точками называют точки в которых
производная равна 0);
4) если производная положительна в промежутке, лежащем слева от данной
стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то
данная точка есть точка максимума функции, если же производная отрицательна
слева и положительна справа от данной стационарной точки, то данная точка есть
точка минимума функции; если производная имеет один и тот же знак как слева,
так и справа от стационарной тонки, то в этой точке нет ни максимума, ни
минимума, функции;
5) заменить в данном выражении функции аргумент значением, которое дает
максимум или минимум функции; получим значение соответственно максимума или
минимума функции.
Если функция имеет точки разрыва, то эти точки должны быть включены в число
стационарных точек, разбивающих Ох на промежутки, в которых определяется знак
производной.
6.4.Точка перегиба графика функции.
Будем говорить, что кривая y = f(x) в точке x0 обращена
выпуклостью вверх, если существует такая окрестность точки x0
, что часть кривой, соответствующая этой окрестности, лежит под касательной к
этой кривой, проведенной в точке A с абсциссой x0.
(см. Рисунок 1а).
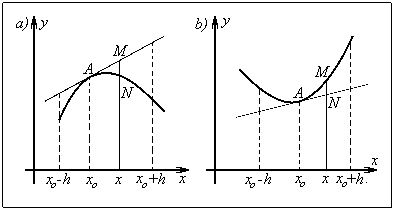 Рисунок 1 Рисунок 1 |
Будем говорить, что кривая y = f(x) в точке x0 обращена
выпуклостью вниз, если существует такая окрестность точки x0
, что часть кривой, соответствующая этой окрестности, лежит над касательной к
этой кривой, проведенной в точке A с абсциссой x0.
(см. Рисунок 1б).
Из определения выпуклости вверх (вниз) кривой y = f(x) в точке x
0 следует, что для любой точки x из интервала (x0
- h, x0 + h), не совпадающей с точкой x0,
имеет место неравенство f(x) - y < 0 ( f(x) - y > 0) где
f(x) - ордината точки M кривой y = f(x), y -
ордината точки N касательной
y - y0 = f '(x0 )(x - x0 ) к данной кривой
в точке A. (смотри рисунок 1, а, б).
Ясно, что и наоборот, если для любой точки x интервала (x0
- h, x0 + h), не совпадающей с x0, выполняется
неравенство f(x) - y < 0 (f(x) - y > 0),
то кривая y = f(x) в точке x0 обращена выпуклостью вверх (вниз).
Будем называть кривую y = f(x) выпуклой вверх (вниз) в интервале (a,
b), если она выпукла вверх (вниз) в каждой точке этого интервала.
Если кривая y = f(x) обращена выпуклостью вверх в интервале (a, b)
, то с увеличением аргумента x угловой коэффициент касательной к этой
кривой в точке с абсциссой x будет уменьшаться.
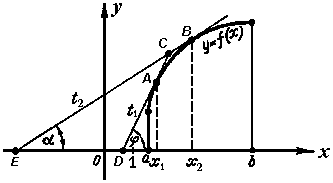
Рисунок 2. |
В самом деле, пусть абсцисса x1 точки A меньше
абсциссы x2 точки B (рис. 2). Проведем касательные
t1 и t2 соответствено в точках A и
B к кривой y = f(x). Пусть a и j - углы наклона касательных t
1 и t2. Тогда из рис. 2 видим, что j - внешний угол
треугольника ECD, а поэтому он больше угла a. Следовательно tgj
> tga или f '(x1 ) > f '(x2 ).
Таким образом мы показали, что если в интервале (a, b) кривая y =
f(x) обращена выпуклостью вверх, то с увеличением аргумента x
функция y = f '(x) убывает. Поэтому вторая производная f ''(x)
функции f(x), как производная убывающей фунции f '(x), будет
отрицательна или равна нулю в интервале (a, b): f ''(x)
£0.
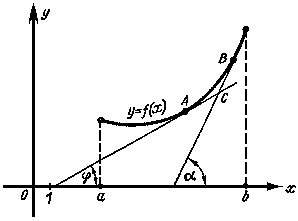
Рисунок 3. |
Если кривая y = f(x) обращена выпуклостью вниз, то из рис.2
непосредственно видно, что tga > tgj т.е. f '(x2
) > f '(x1 ), а поэтому в интервале (a, b) производная
f '(x) возрастает. Тогда вторая производная f ''(x) функции f
(x), как производная возрастающей в интервале (a, b) функции f
'(x), будет положительна или равна нулю: f ''(x)³0.
Докажем, что и наоборот, если f ''(x)£0 в некотором интервале
(a, b), то в этом интервале кривая y = f (x) обращена выпуклостью
вверх; если f ''(x)³0 в интервале (a, b), то в этом
интервале кривая обращена выпуклостью вниз.
Запишем уравнение касательной y - y0 = f '(x0 )(x - x
0 ) к кривой y = f (x) в точке x0, где
a < x0 b, в виде y = y0 + f '(x0 )(x
- x0 ). Очевидно, y0 = f(x0 ), а
потому последнее уравнение можно записать в виде
y = f(x0 ) + f '(x0 )(x - x0 ). (1)
Но, согласно формуле Тейлора, при n = 2 имеем:
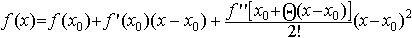 (2)
Фиксируя x в интервале (a, b) и вычитая почленно из уравнения
(2) уравнение (1), получим:
(2)
Фиксируя x в интервале (a, b) и вычитая почленно из уравнения
(2) уравнение (1), получим: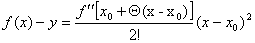 (3)
Если f ''[x0 + Q(x - x0 )]£0, где 0 < Q < 1, то имеем f(x) - y £ 0
откуда следует, что кривая y = f(x) в точке x обращена выпуклостью вверх.
Если f ''[x0 + Q(x - x0 )]³0
, то имеем f(x) - y ³ 0 откуда следует, что кривая y
= f(x) в точке x обращена выпуклостью вниз.
Так как была зафиксирована произвольная точка x интервала (a, b)
, то высказанное выше утверждение доказано.
(3)
Если f ''[x0 + Q(x - x0 )]£0, где 0 < Q < 1, то имеем f(x) - y £ 0
откуда следует, что кривая y = f(x) в точке x обращена выпуклостью вверх.
Если f ''[x0 + Q(x - x0 )]³0
, то имеем f(x) - y ³ 0 откуда следует, что кривая y
= f(x) в точке x обращена выпуклостью вниз.
Так как была зафиксирована произвольная точка x интервала (a, b)
, то высказанное выше утверждение доказано.
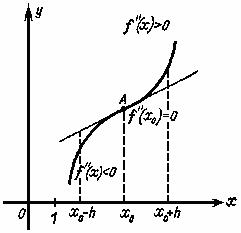
Рисунок 4. |
Точка кривой, в которой кривая меняет направление изгиба, т.е. переходит от
выпуклости вверх к выпуклости вниз или наоборот, называется точкой перегиба
кривой (рис.4). (В этом определении предполагается, что в точке перехода
кривой от выпуклости вверх к выпуклости вниз (или наоборот) имеется
единственная касательная).
Теорема 8. Пусть функция f(x) имеет непрерывную вторую производную f
''(x) и пусть A[x0 ; f(x0 )] -
точка перегиба кривой y = f(x). Тогда f ''(x0 ) = 0 или не
существует.
Доказательство. Рассмотрим для определенности случай, когда кривая
y = f(x) в точке перегиба A[x0 ; f(x0 )
] переходит от выпуклости вверх в выпуклости вниз (рис.4). Тогда при достаточно
малом h в интервале (x0 - h, x0 ) вторая
производная f ''(x) будет меньше нуля, а в инетрвале (x0
, x0 +h) - больше нуля.
Но f ''(x) - функция непрерывная, а потому, переходя от отрицательных
значений к положительным, она при x = x0 обращается в нуль:
f ''(x0 ) = 0.
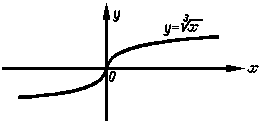
Рисунок 5. |
На рис.5 изображен график функции 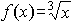 . Хотя при x0 = 0 имеется касательная и точка перегиба, все
же вторая производная f ''(x) не равна нулю, она даже не существует в
этой точке. В самом деле, имеем
. Хотя при x0 = 0 имеется касательная и точка перегиба, все
же вторая производная f ''(x) не равна нулю, она даже не существует в
этой точке. В самом деле, имеем 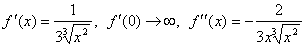 Итак, f ''(0) не существует. Но тем не менее точка O(0; 0)
является точкой перегиба, так как при x < 0 f ''(x) > 0 и кривая
выпукла вниз, а при x > 0 f ''(x) < 0 и кривая выпукла вверх.
Таким образом в случае непрерывности второй производной f ''(x)
обращение в нуль или несуществование ее в какой-нибудь точки кривой y = f(x)
является необходимым условием существования точки перегиба. Однако это
условие не является достаточным.
Теорема 9. Если вторая производная f ''(x) непрерывна и меняет знак
при x = x0, то точка A[x0 ; f(x0
)] является точкой перегиба кривой y = f(x) при условии, конечно, что в
точке A существует касательная.
Доказательство. Пусть например f ''(x) < 0 при x
0 - h < x < x0 и f ''(x) > 0 при x
0 < x < x0 + h. Тогда в интервале (x0
- h; x0 ) кривая y = f(x) обращена выпуклостью вверх, а в
интервале (x0 ; x0 + h) - выпклостью вниз (смотри
рис.4), т.е. точка A[x0 ; f(x0 )] есть
точка перегиба кривой, что и требовалось доказать.
6.5.Общая схема исследования функции и построение ее графика.
1. Находим область определения функции f(x)
2. Находим точки пересечения кривой y = f(x) с осями координат и наносим
их на чертеж.
3. Определяем, симметрична ли кривая y = f(x) относительно осей
координат и начала координат.
4. Исследуем функцию y = f(x) на непрерывность. Если функция имеет в
точке x0 разрыв, то отмечаем ее на чертеже.
5. Находим асимптоты кривой, если они имеются.
6. Находим максимум и минимум функции и отмечаем на чертеже точки кривой с
максимальной и минимальной ординатами.
7. Исследуем кривую y = f(x) на выпуклость вверх или вниз, находим точки
перегиба кривой и отмечаем их на чертеже.
8. Вычерчиваем кривую y = f(x).
Итак, f ''(0) не существует. Но тем не менее точка O(0; 0)
является точкой перегиба, так как при x < 0 f ''(x) > 0 и кривая
выпукла вниз, а при x > 0 f ''(x) < 0 и кривая выпукла вверх.
Таким образом в случае непрерывности второй производной f ''(x)
обращение в нуль или несуществование ее в какой-нибудь точки кривой y = f(x)
является необходимым условием существования точки перегиба. Однако это
условие не является достаточным.
Теорема 9. Если вторая производная f ''(x) непрерывна и меняет знак
при x = x0, то точка A[x0 ; f(x0
)] является точкой перегиба кривой y = f(x) при условии, конечно, что в
точке A существует касательная.
Доказательство. Пусть например f ''(x) < 0 при x
0 - h < x < x0 и f ''(x) > 0 при x
0 < x < x0 + h. Тогда в интервале (x0
- h; x0 ) кривая y = f(x) обращена выпуклостью вверх, а в
интервале (x0 ; x0 + h) - выпклостью вниз (смотри
рис.4), т.е. точка A[x0 ; f(x0 )] есть
точка перегиба кривой, что и требовалось доказать.
6.5.Общая схема исследования функции и построение ее графика.
1. Находим область определения функции f(x)
2. Находим точки пересечения кривой y = f(x) с осями координат и наносим
их на чертеж.
3. Определяем, симметрична ли кривая y = f(x) относительно осей
координат и начала координат.
4. Исследуем функцию y = f(x) на непрерывность. Если функция имеет в
точке x0 разрыв, то отмечаем ее на чертеже.
5. Находим асимптоты кривой, если они имеются.
6. Находим максимум и минимум функции и отмечаем на чертеже точки кривой с
максимальной и минимальной ординатами.
7. Исследуем кривую y = f(x) на выпуклость вверх или вниз, находим точки
перегиба кривой и отмечаем их на чертеже.
8. Вычерчиваем кривую y = f(x).
6.6. Касательная и нормаль к плоской кривой.
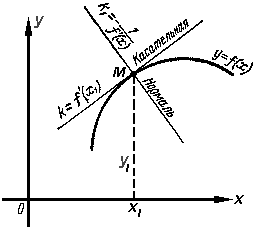 Пусть даны кривая y = f(x) и точка M (x1 ; y1)
на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).
Как известно, угловой коэффициент k касательной к кривой y = f(x)
в точке M (x1 ; y1) равен значению f '(x1
) производной y' = f '(x) при x = x1/
Следовательно, уравнение касательной можно записать в виде уравнения прямой,
проходящей через данную точку в данном направлении, т.е. в виде
y - y1 = f '(x1)(x - x1)
Нормалью называется прямая, проходящая через точку касания
перпендикулярно касательной. поэтому ее угловой коэффициент равен
Пусть даны кривая y = f(x) и точка M (x1 ; y1)
на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).
Как известно, угловой коэффициент k касательной к кривой y = f(x)
в точке M (x1 ; y1) равен значению f '(x1
) производной y' = f '(x) при x = x1/
Следовательно, уравнение касательной можно записать в виде уравнения прямой,
проходящей через данную точку в данном направлении, т.е. в виде
y - y1 = f '(x1)(x - x1)
Нормалью называется прямая, проходящая через точку касания
перпендикулярно касательной. поэтому ее угловой коэффициент равен 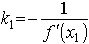 , а уравнение записывается в виде
, а уравнение записывается в виде 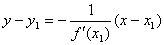
7.Экономическое приложение производной. 7.1.Экономическая
интерпретация производной
В экономической теории активно используется понятие «маржинальный», что означает
«предельный». Введение этого понятия в научный оборот в XIX веке позволило
создать совершенно новый ин
струмент исследования и опи
сания экономических явлений - инструмент, по
средством которого стало возможно ставить и
решать новый класс научных проблем.
Классическая экономическая теория Смита, Рикардо,
Милля обычно имела дело со
средними величинами: средняя цена,
средняя производительность труда и т.д. Но постепенно
сложился иной подход. Существенные
закономерности оказалось можно обнаружить в области
предельных величин.
Предельные или пограничные величины характеризуют не с
остояние (как суммарная
или средняя величины.),
а процесс, изменение экономического объекта. Следов
ательно, производная выст
упает как интенсивность изменения некоторого
экономического объекта (процесса) по времени или относител
ьно другого исследу
емого фактора.
Надо заметить, что экономика не всегда позволяет ис
пользовать предельные величины в силу прерывности (дискретности) экономических
показателей во времени (например, годовых, квартальных, месячных и т.д.). В то
же время во многих случаях можно отвлечься от дискретности и эффективно
использовать предельные величины.
Рассмотрим ситуацию: пусть y - издержки производства, а х -
количество продукции, тогда Dx- прирост продукции, а Dy -
приращение издержек производства.
В этом случае производная 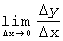 выражает предельные издержки производства и характеризует приближенно
дополнительные затраты на производство дополнительной единицы продукции
выражает предельные издержки производства и характеризует приближенно
дополнительные затраты на производство дополнительной единицы продукции 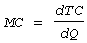 ,где MC – предельные издержки (marginal costs); TC – общие издержки (total
costs); Q - количество.
,где MC – предельные издержки (marginal costs); TC – общие издержки (total
costs); Q - количество.
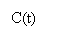 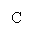  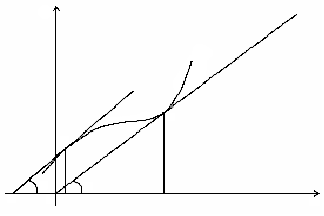  Геометрическая интерпретация предельных издержек - это тангенс угла наклона
касательной к кривой в данной точке (см. рис.).
Геометрическая интерпретация предельных издержек - это тангенс угла наклона
касательной к кривой в данной точке (см. рис.).
  Аналогичным образом могут быть определены и многие другие экономические
величины, имеющие предельный характер.
Аналогичным образом могут быть определены и многие другие экономические
величины, имеющие предельный характер.
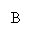 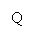 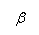 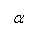 Другой пример - категория предельной выручки (MR— marginal revenue) — это
дополнительный доход, полученный при переходе от производства n-ной к (n+1)-ой
единице продукта.
Она представляет собой первую производную от выручки:
Другой пример - категория предельной выручки (MR— marginal revenue) — это
дополнительный доход, полученный при переходе от производства n-ной к (n+1)-ой
единице продукта.
Она представляет собой первую производную от выручки: 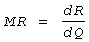 .
При этом R= PQ, где R–выручка (revenue); P–цена (price).
Таким образом .
При этом R= PQ, где R–выручка (revenue); P–цена (price).
Таким образом 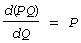 , Þ MR= P.
Это равенство верно относительно условий совершенной конкуренции, когда
экономические агенты каждый по отдельности не могут оказать влияния на цену.
Обратимся к теориям потребления: кардиналистской и ординалистской.
Кардиналистский (количественный) подход к теории цен предполагает равное
влияние величин полезности товара и затрат на его производства на
формирование цены. В основе рассматриваемого подхода - исследования А.
Маршалла.
Ординалистский (Порядковый) подход к теории цен разрабатывался И. Фишером, В.
Парето. Суть данного подхода состоит в том, что потребители, имеющие
определенный уровень доходов, сравнивают между собой цены и полезность
различных наборов экономических благ и отдают предпочтение тем наборам,
которые при сравнительно низких ценах имеют максимальную полезность для
конкретного потребителя.
В соответствии с первой, суммарную полезность U для любого субъекта,
если в экономике существует n потребительских благ в объемах х
1, x2,. хn, можно выразить в виде
кардиналистской функции полезности:
U= U(х1, x2,. xn).
Предельные полезности MU товаров выступают в качестве ее частных
производных: , Þ MR= P.
Это равенство верно относительно условий совершенной конкуренции, когда
экономические агенты каждый по отдельности не могут оказать влияния на цену.
Обратимся к теориям потребления: кардиналистской и ординалистской.
Кардиналистский (количественный) подход к теории цен предполагает равное
влияние величин полезности товара и затрат на его производства на
формирование цены. В основе рассматриваемого подхода - исследования А.
Маршалла.
Ординалистский (Порядковый) подход к теории цен разрабатывался И. Фишером, В.
Парето. Суть данного подхода состоит в том, что потребители, имеющие
определенный уровень доходов, сравнивают между собой цены и полезность
различных наборов экономических благ и отдают предпочтение тем наборам,
которые при сравнительно низких ценах имеют максимальную полезность для
конкретного потребителя.
В соответствии с первой, суммарную полезность U для любого субъекта,
если в экономике существует n потребительских благ в объемах х
1, x2,. хn, можно выразить в виде
кардиналистской функции полезности:
U= U(х1, x2,. xn).
Предельные полезности MU товаров выступают в качестве ее частных
производных: 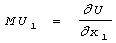 . Они
показывают, на сколько изменяется полезность всей массы благ, достающихся
субъекту, при бесконечно малом приращении количества блага i (i=1,2.n)
В ординалистской теории полагается, что потребитель оценивает полезность не
отдельных благ, а потребительских наборов; что он способен сопоставить
полезности наборов товаров.
Ординалистская функция полезности исследована подробно, значительный вклад в
ее изучение внес Дж. Хикс. После его трудов началось прогрессирующее
вытеснение понятия "предельная полезность" категорией предельной нормы
замещения (MRS – marginal rate of substitution).
Предположим, что происходит замещение товара y товаром х при
движении сверху вниз вдоль кривой безразличия. Предельная норма замещения
товара y товаром x показывает, какое количество товара x
необходимо для того, чтобы компенсировать потребительскую утрату единицы товара
y.
Они определяются так: . Они
показывают, на сколько изменяется полезность всей массы благ, достающихся
субъекту, при бесконечно малом приращении количества блага i (i=1,2.n)
В ординалистской теории полагается, что потребитель оценивает полезность не
отдельных благ, а потребительских наборов; что он способен сопоставить
полезности наборов товаров.
Ординалистская функция полезности исследована подробно, значительный вклад в
ее изучение внес Дж. Хикс. После его трудов началось прогрессирующее
вытеснение понятия "предельная полезность" категорией предельной нормы
замещения (MRS – marginal rate of substitution).
Предположим, что происходит замещение товара y товаром х при
движении сверху вниз вдоль кривой безразличия. Предельная норма замещения
товара y товаром x показывает, какое количество товара x
необходимо для того, чтобы компенсировать потребительскую утрату единицы товара
y.
Они определяются так: 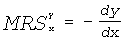 .
Т.к. dy отрицательно, знак "-" вводится, чтобы MRS была больше нуля.
Итак, предельная норма замещения геометрически есть касательная к кривой
безразличия в данной точке. Значение предельной нормы замещения по абсолютной
величине равно тангенсу угла наклона касательной к кривой безразличия.
Приведем еще один пример элементарного анализа на микроуровне, который имеет
аналог и на макроуровне.
Любой индивид свой доход Y после уплаты налогов использует на
потребление C и сбережение S. Ясно, что лица с низким
доходом, как правило, целиком используют его на потребление, так что размер
сбережения равен нулю. С ростом дохода субъект не только больше потребляет, но
и больше сберегает. Как установлено теорией и подтверждено эмпирическими
исследования, потребление и сбережение зависят от размера дохода:
Y= C(Y) + S(Y).
Зависимость потребления индивида от дохода называется функцией склонности к
потреблению или функцией потребления.
Использование производной позволяет определить такую категорию, как предельную
склонность к потреблению MPC (marginal property to consume), показывающую долю
прироста личного потребления в приросте дохода: .
Т.к. dy отрицательно, знак "-" вводится, чтобы MRS была больше нуля.
Итак, предельная норма замещения геометрически есть касательная к кривой
безразличия в данной точке. Значение предельной нормы замещения по абсолютной
величине равно тангенсу угла наклона касательной к кривой безразличия.
Приведем еще один пример элементарного анализа на микроуровне, который имеет
аналог и на макроуровне.
Любой индивид свой доход Y после уплаты налогов использует на
потребление C и сбережение S. Ясно, что лица с низким
доходом, как правило, целиком используют его на потребление, так что размер
сбережения равен нулю. С ростом дохода субъект не только больше потребляет, но
и больше сберегает. Как установлено теорией и подтверждено эмпирическими
исследования, потребление и сбережение зависят от размера дохода:
Y= C(Y) + S(Y).
Зависимость потребления индивида от дохода называется функцией склонности к
потреблению или функцией потребления.
Использование производной позволяет определить такую категорию, как предельную
склонность к потреблению MPC (marginal property to consume), показывающую долю
прироста личного потребления в приросте дохода: 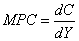 .
По мере увеличения доходов MPC уменьшается. Последовательно определяя
сбережения при каждом значении дохода, можно построить функцию склонности к
сбережению или функцию сбережения. Долю прироста сбережений в приросте
дохода показывает предельная склонность к сбережению MPS(marginal propensity to
save):
.
По мере увеличения доходов MPC уменьшается. Последовательно определяя
сбережения при каждом значении дохода, можно построить функцию склонности к
сбережению или функцию сбережения. Долю прироста сбережений в приросте
дохода показывает предельная склонность к сбережению MPS(marginal propensity to
save): 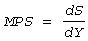 .
С увеличением доходов MPS увеличивается.
Еще одним примером использования производной в экономике является анализ
производственной функции. Поскольку ограниченность ресурсов принципиально не
устранима, то решающее значение приобретает отдача от факторов производства.
Здесь также применима производная, как инструмент исследования. Пусть
применяемый капитал постоянен, а затраты труда увеличиваются. Можно ввести в
экономический анализ следующую категорию - предельный продукт труда MPL
(marginal product of labor) – это дополнительный продукт, полученный в
результате дополнительных вложений труда (L – labor) при неизменной величине
капитала:
.
С увеличением доходов MPS увеличивается.
Еще одним примером использования производной в экономике является анализ
производственной функции. Поскольку ограниченность ресурсов принципиально не
устранима, то решающее значение приобретает отдача от факторов производства.
Здесь также применима производная, как инструмент исследования. Пусть
применяемый капитал постоянен, а затраты труда увеличиваются. Можно ввести в
экономический анализ следующую категорию - предельный продукт труда MPL
(marginal product of labor) – это дополнительный продукт, полученный в
результате дополнительных вложений труда (L – labor) при неизменной величине
капитала: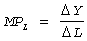 .
Если вложения осуществляются достаточно малыми порциями, то .
Если вложения осуществляются достаточно малыми порциями, то 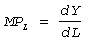 , т.к. dY - результат, dL - затраты, то MPL – предельная
производительность труда.
Аналогично, MPk - предельный продукт капитала -
дополнительный продукт, полученный в результате дополнительных вложений
капитала K при неизменной величине труда:
, т.к. dY - результат, dL - затраты, то MPL – предельная
производительность труда.
Аналогично, MPk - предельный продукт капитала -
дополнительный продукт, полученный в результате дополнительных вложений
капитала K при неизменной величине труда: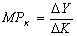 .
Если вложения осуществляются малыми порциями, то
.
Если вложения осуществляются малыми порциями, то 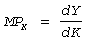 .
MPk - характеризует предельную производительность капитала.
Для исследования экономических процессов и решения других прикладных задач часто
используется понятие эластичности функции.
Определение: Эластичностью функции Еx(y)
называется предел отношения относительного приращения функции y к
относительному приращению переменной x при Dx®0: .
MPk - характеризует предельную производительность капитала.
Для исследования экономических процессов и решения других прикладных задач часто
используется понятие эластичности функции.
Определение: Эластичностью функции Еx(y)
называется предел отношения относительного приращения функции y к
относительному приращению переменной x при Dx®0:
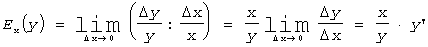 .
Эластичность функции показывает приближенно, на сколько процентов изменится
функция y= f(x), при изменении независимой переменной x на 1%.
Приведем несколько конкретных иллюстраций такой зависимости. Прямой коэффициент
эластичности спроса по цене устанавливает, на сколько процентов увеличивается
(уменьшается) спрос Q на товар i при уменьшении (увеличении)
его цены P на 1%:
.
Эластичность функции показывает приближенно, на сколько процентов изменится
функция y= f(x), при изменении независимой переменной x на 1%.
Приведем несколько конкретных иллюстраций такой зависимости. Прямой коэффициент
эластичности спроса по цене устанавливает, на сколько процентов увеличивается
(уменьшается) спрос Q на товар i при уменьшении (увеличении)
его цены P на 1%: 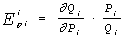 .
Перекрестный коэффициент эластичности спроса по цене
.
Перекрестный коэффициент эластичности спроса по цене 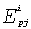 показывает, на сколько процентов изменится спрос на товар i при
однопроцентных колебаниях цены товара j (j = 1,2,.n):
показывает, на сколько процентов изменится спрос на товар i при
однопроцентных колебаниях цены товара j (j = 1,2,.n): 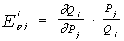 .
Количественную сторону взаимодействия дохода и спроса отражает коэффициент
эластичности спроса по доходу, который указывает, на сколько процентов
изменится спрос на i-тый товар Qi если доход,
предназначенный на текущее потребление, изменится на 1%:
.
Количественную сторону взаимодействия дохода и спроса отражает коэффициент
эластичности спроса по доходу, который указывает, на сколько процентов
изменится спрос на i-тый товар Qi если доход,
предназначенный на текущее потребление, изменится на 1%: 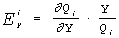 .
Можно привести и другие примеры использования производной при фокусировке
различных категорий и закономерностей. Дальнейшее раскрытие экономического
смысла хотелось бы осуществить через рассмотрение экономической интерпретации
математических теорем.
.
Можно привести и другие примеры использования производной при фокусировке
различных категорий и закономерностей. Дальнейшее раскрытие экономического
смысла хотелось бы осуществить через рассмотрение экономической интерпретации
математических теорем.
7.2. Применение производной в экономической теории.
Проанализировав экономический смысл производной, нетрудно заметить, что
многие, в том числе базовых законы теории производства и потребления, спроса
и предложения оказываются прямыми следствиями математических теорем.
Вначале рассмотрим экономическую интерпретацию теоремы: если дифференцируемая на
промежутке X функция y= f(x) достигает наибольшего или
наименьшего значения во внутренней точке x0 этого
промежутка, то производная функции в этой точке равна нулю, то есть f’(x0
) = 0.
Один из базовых законов теории производства звучит так: "Оптимальный для
производителя уровень выпуска товара определяется равенством предельных
издержек и предельного дохода".
То есть уровень выпуска Qo является оптимальным для
производителя, если MC(Qo)=MR(Qo), где MC
- предельные издержки, а MR - предельный доход.
Обозначим функцию прибыли за П(Q). Тогда П(Q) = R(Q) — C(Q), где R –
прибыль, а C – общие издержки производства.
Очевидно, что оптимальным уровнем производства является тот, при котором прибыль
максимальна, то есть такое значение выпуска Qo, при котором функция
П(Q) имеет экстремум (максимум). По теореме Ферма в этой точке П’(Q) = 0. Но
П’(Q)=R’(Q) - C’(Q), поэтому R’(Qo) = C’(Qo), откуда
следует, что MR(Qo) = MC(Qo).
Другое важное понятие теории производства - это уровень наиболее экономичного
производства, при котором средние издержки по производству товара минимальны.
Соответствующий экономический закон гласит: “оптимальный объем производства
определяется равенством средних и предельных издержек”.
Получим это условие как следствие сформулированной выше теоремы. Средние
издержки AC(Q) определяются как 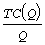 , т.е. издержки по производству всего товара, деленные на произведенное его
количество. Минимум этой величины достигается в критической точке функции
y=AC(Q), т.е. при условии
, т.е. издержки по производству всего товара, деленные на произведенное его
количество. Минимум этой величины достигается в критической точке функции
y=AC(Q), т.е. при условии 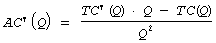 , откуда TC’(Q)Q—TC(Q) = 0 или
, откуда TC’(Q)Q—TC(Q) = 0 или 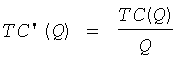 , т.е. MC(Q)=AC(Q).
Понятие выпуклости функции также находит свою интерпретацию в экономической
теории.
Один из наиболее знаменитых экономических законов - закон убывающей
доходности - звучит следующим образом: "с увеличением производства
дополнительная продукция, полученная на каждую новую единицу ресурса
(трудового, технологического и т.д.), с некоторого момента убывает".
Иными словами, величина
, т.е. MC(Q)=AC(Q).
Понятие выпуклости функции также находит свою интерпретацию в экономической
теории.
Один из наиболее знаменитых экономических законов - закон убывающей
доходности - звучит следующим образом: "с увеличением производства
дополнительная продукция, полученная на каждую новую единицу ресурса
(трудового, технологического и т.д.), с некоторого момента убывает".
Иными словами, величина 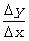 , где Dy - приращение выпуска продукции, а Dx - приращение ресурса, уменьшается
при увеличении x. Таким образом, закон убывающей доходности
формулируется так: функция y= f(x), выражающая зависимость выпуска
продукции от вложенного ресурса, является функцией, выпуклой вверх.
Другим базисным понятием экономической теории является функция полезности U=
U(x), где х - товар, а U – полезность (utility). Эта
величина очень субъективная для каждого отдельного потребителя, но достаточно
объективная для общества в целом. Закон убывающей полезности звучит следующим
образом: с ростом количества товара, дополнительная полезность от каждой новой
его единицы с некоторого момента убывает. Очевидно, этот закон можно
переформулировать так: функция полезности является функцией, выпуклой вверх. В
такой постановке закон убывающей полезности служит отправной точкой для
математического исследования теории спроса и предложения.
7.3. Использование производной для решения задач по экономической теории.
Задача 1.
Цементный завод производит Х т. цемента в день. По договору он должен
ежедневно поставлять строительной фирме не менее 20 т. цемента.
Производственные мощности завода таковы, что выпуск цемента не может
превышать 90 т. в день.
Определить, при каком объеме производства удельные затраты будут наибольшими
(наименьшими), если функция затрат имеет вид:
К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200
Наша задача сводится к отысканию наибольшего и наименьшего значения функции У=
-х2+98х+200. На промежутке [20;90].
Вывод: x=49, критическая точка функции. Вычисляем значение функции на концах
промежутках и в критической точке.
f(20)=1760 f(49)=2601 f(90)=320.
Таким образом, при выпуске 49 тонн цемента в день удельные издержки
максимальны, это экономически не выгодно, а при выпуске 90 тонн в день
минимально, следовательно можно посоветовать работать заводу на предельной
мощности и находить возможности усовершенствовать технологию, так как дальше
будет действовать закон убывающей доходности. И без реконструкции нельзя
будет увеличить выпуск продукции.
, где Dy - приращение выпуска продукции, а Dx - приращение ресурса, уменьшается
при увеличении x. Таким образом, закон убывающей доходности
формулируется так: функция y= f(x), выражающая зависимость выпуска
продукции от вложенного ресурса, является функцией, выпуклой вверх.
Другим базисным понятием экономической теории является функция полезности U=
U(x), где х - товар, а U – полезность (utility). Эта
величина очень субъективная для каждого отдельного потребителя, но достаточно
объективная для общества в целом. Закон убывающей полезности звучит следующим
образом: с ростом количества товара, дополнительная полезность от каждой новой
его единицы с некоторого момента убывает. Очевидно, этот закон можно
переформулировать так: функция полезности является функцией, выпуклой вверх. В
такой постановке закон убывающей полезности служит отправной точкой для
математического исследования теории спроса и предложения.
7.3. Использование производной для решения задач по экономической теории.
Задача 1.
Цементный завод производит Х т. цемента в день. По договору он должен
ежедневно поставлять строительной фирме не менее 20 т. цемента.
Производственные мощности завода таковы, что выпуск цемента не может
превышать 90 т. в день.
Определить, при каком объеме производства удельные затраты будут наибольшими
(наименьшими), если функция затрат имеет вид:
К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200
Наша задача сводится к отысканию наибольшего и наименьшего значения функции У=
-х2+98х+200. На промежутке [20;90].
Вывод: x=49, критическая точка функции. Вычисляем значение функции на концах
промежутках и в критической точке.
f(20)=1760 f(49)=2601 f(90)=320.
Таким образом, при выпуске 49 тонн цемента в день удельные издержки
максимальны, это экономически не выгодно, а при выпуске 90 тонн в день
минимально, следовательно можно посоветовать работать заводу на предельной
мощности и находить возможности усовершенствовать технологию, так как дальше
будет действовать закон убывающей доходности. И без реконструкции нельзя
будет увеличить выпуск продукции.
Задача 2.
Задача: Предприятие производит Х единиц некоторой однородной продукции в
месяц. Установлено, что зависимость финансовых накопления предприятия от
объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать
потенциал предприятия.
Функция исследуется с помощью производной. Получаем, что при Х=100 функция
достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема
производства до 100 единиц, при х =100 они достигают максимума и объем
накопления равен 39000 денежных единиц. Дальнейший рост производства приводит
к сокращению финансовых накоплений.
Задача 3.
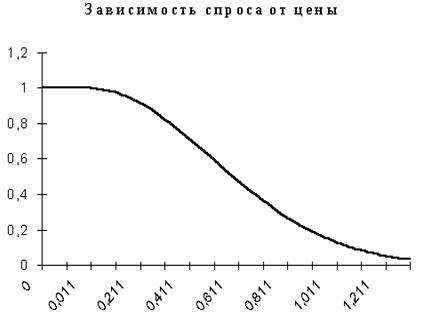
Спрос-это зависимость между ценой единицы товара и количеством товара,
которое потребители готовы купить при каждой возможной цене, за определенный
период времени и при прочих равных условиях.
Зависимость спроса от цены описывается функцией 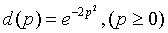 ,
Данная функция исследуется с помощью производной: ,
Данная функция исследуется с помощью производной: 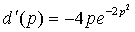 Производная меньше нуля, если P>=0.
Определим точку перегиба функции. Такой точкой является точка (0,5;0,6),
т.е. при P<1/2 спрос убывает медленнее, а при P>1/2 спрос убывает все
быстрее.
Производная меньше нуля, если P>=0.
Определим точку перегиба функции. Такой точкой является точка (0,5;0,6),
т.е. при P<1/2 спрос убывает медленнее, а при P>1/2 спрос убывает все
быстрее.
Задача 4.
Выручка от реализации товара по цене p составляет: 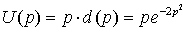 (Денежных единиц), где
(Денежных единиц), где 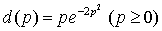 . Исследуем эту функцию с помощью производной.
Производная этой функции: . Исследуем эту функцию с помощью производной.
Производная этой функции: 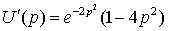 положительна, если p<1/2 и отрицательна для p>1/2, это означает, что с
ростом цены выручка в начале увеличивается ( несмотря на падение спроса) и
p=1/2 достигает максимального значения
положительна, если p<1/2 и отрицательна для p>1/2, это означает, что с
ростом цены выручка в начале увеличивается ( несмотря на падение спроса) и
p=1/2 достигает максимального значения 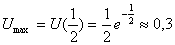 , дальнейшее увеличение цены не имеет смысла, т.как оно ведет к сокращению
выручки. Темп изменения выручки выражается второй производной.
, дальнейшее увеличение цены не имеет смысла, т.как оно ведет к сокращению
выручки. Темп изменения выручки выражается второй производной.
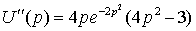
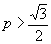 темп положительный темп положительный 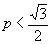 темп отрицательный
На промежутке (0,1/2) функция возрастает все медленнее, то есть дальнейшее
повышение цены не выгодно. Сначала выручка убывает с отрицательным темпом для темп отрицательный
На промежутке (0,1/2) функция возрастает все медленнее, то есть дальнейшее
повышение цены не выгодно. Сначала выручка убывает с отрицательным темпом для 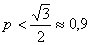 , а затем темп убывания становится положительным и для P>0,9 выручка убывает
все быстрее и приближается к нулю при неограниченном увеличении цены.
Для наглядной демонстрации выше сказанного составим таблицу и построим график.
, а затем темп убывания становится положительным и для P>0,9 выручка убывает
все быстрее и приближается к нулю при неограниченном увеличении цены.
Для наглядной демонстрации выше сказанного составим таблицу и построим график.
| p | (0, 1/2) | 1/2 | 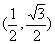
| 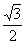
| 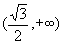
| | U'(p) | + | 0 | - | -0,47 | - | | U''(p) | - | | - | 0 | + | | U (p) | возрастает выпукла | 0,3 max | убывает выпукла | 0,2 точка перегиба | убывает вогнута |
Страницы: 1, 2, 3, 4
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



