Реферат: Развитие аналитической геометрии

МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. А. А. КУЛЕШОВА

Реферат

Развитие аналитической геометрии

Выполнила

студентка

Гуленкова Оксана

Могилев 2002.

Алгебраические методы в геометрии

Применение алгебры в геометрии имело к началу XVII в. долгую исто­рию. Еще

древние вавилоняне решали многие задачи на прямоугольные треугольники,

выражая искомые отрезки, как корни численных квадрат­ных уравнений;

аналогичные приемы употреблялись впоследствии неодно­кратно. В классической!

Греции важным средством геометрического исследования, в частности конических

сечений, служила геометриче­ская алгебра, в которой место вычислений занимали

построения от­резков.

Бурные успехи символической и числовой алгебры в XVI в. явились основой

гораздо более обширных приложений алгебраического метода в геометрии,

приведших к созданию новой аналитической геометрии. Пер­воначально работы в

этом направлении не выходили за пределы тради­ционных постановок и решений

вопросов, иногда довольно сложных. Большое число таких задач было рассмотрено

Виетом, за которым по­следовали и другие, например Марин Геталдич (Гетальди,

1566—1627), уроженец югославского города Дубровник (Рагуза), в то время

бывшего самостоятельной республикой. Ученик Хр. Клавия и хороший знаток

греческих авторов, Гетальди испытал особенно сильное влияние Виета, с которым

познакомился в бытность в Париже. В «Собрании различных задач» (Variorum

problematum collectio, Veneliae, 1607) и посмертно из­данном труде «О

математическом анализе и синтезе» (De resolutione et compositione

mathematica, Romae, 1630) Гетальди средствами алгебры Ви­ета решает

разнообразные задачи на деление отрезков, построение тре­угольников и так

называемые вставки (ср. т. I, стр. 84); по большей части его задачи

выражаются уравнениями первой или второй степени относи­тельно искомого

неизвестного отрезка. В некоторых случаях применяется чисто геометрическое

решение. Упомянем античную задачу о вставке между продолжением стороны

квадрата и ближайшей перпендикулярной стороной отрезка данной длины,

продолжение которого проходит через вершину квадрата, не лежащую на названных

сторонах. Гетальди отнес задачу к тем, которые не относятся к алгебре (sub

algebram non cadunt), и решил ее геометрически. Данная задача привлекла

внимание и других ученых. Жирар (1629) выразил ее уравнением четвертой

степени и по­казал, как связан выбор знаков перед радикалами, входящими в его

кор­ни, с положением частей искомого отрезка. Декарт (1637) рассмотрел ее с

целью привести пример уравнения четвертой степени, распадающегося на два

квадратных (коэффициенты которых, между прочим, квадратично ир­рациональны

относительно исходных коэффициентов). Попутно Декарт указал, как от более или

менее удачного выбора неизвестной зависит срав­нительная простота уравнения.

Эти соображения Декарта подробнее раз­виты во «Всеобщей арифметике» Ньютона.

Оригинальное решение при­надлежит еще Гюйгенсу.

Алгебраическим решением геометрических задач занимались, как видно, очень

многие. К уже названным можно добавить, например, имя английского алгебраиста

Вильяма Отреда (1574—1660), на книге кото­рого, озаглавленной, подобно одному

из сочинений ал-Каши, «Ключ ма­тематики» (Clavis mathematicae, Londini, 1631)

[1], отразилось несомненное влияние «Собрания различных задач» Гетальди.

Аналитическая геометрия

Описанная алгебраическая трактовка вопросов геометрии подготовля­ла почву для

создания аналитической геометрии, предметом которой яв­ляется уже нс только

нахождение отдельных отрезков, выражаемых кор­нями уравнений с одним

неизвестным, но изучение свойств различных геометрических образов, прежде

всего алгебраических линий и поверхно­стей, выражаемых уравнениями с двумя

или более неизвестными или ко­ординатами.

Координаты появились еще в древности, притом в различных формах, между собой

непосредственно не связанных. С одной стороны, это были географические

координаты, именовавшиеся долготой и широтой, причем положение пунктов земной

по­верхности, изображенной в виде прямоугольника, характеризовалось парой

чисел. Сходными были астрономические координаты, служившие для определения

положения светил на небесной сфере. Другой вид коор­динат представляли собой

отрезки, зависимости между которыми, так называемые симптомы (см. т. I, 130),

выражали определяющие свой­ства этих кривых. В этом случае речь шла не о

числовых координатах любых точек с отсчетом от фиксированного меридиана и

параллели, а об отрезках диаметров и хорд, связанных с точками

рассматриваемой фи­гуры.

Своеобразной разновидностью координат были отрезки широт и долгот в теории

изменения форм Орема. Здесь не было ни числовых коор­динат любых точек, ни

«симптомов», выраженных средствами геометри­ческой алгебры; словесно

сформулированная зависимость между широтой и долготой формы изображалась

плоской линией.

Координатные отрезки древнегреческой геометрии стали известны в Европе частью по

арабским сочинениям, но главным образом по трудам Архимеда и особенно

Аполлония. Параллельные хорды или полухорды, сопряженные некоторому диаметру,

Аполлоний называл, если перевести с греческого, «по порядку проведенными

линиями», а отрезки этого диа­метра от его конца до хорды — «отсеченными на

диаметре по порядку про­веденными (линиями)» (на рис. 6 соответственно у

и x). В своем упоминав­шемся ранее латинском издании «Конических

сечений» (Венеция, 1566) Федориго Коммандино первые

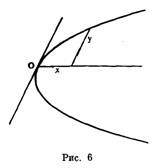
выражения передал оборотом ordinatim applicatae, т. е. «по порядку приложенные»

(т. е. направленные)[2], а вто­рое — quae

ab ipsis ex diametro ad verticem abscinduntur, т. е. «которые отсекаются ими па

диаметре от вершины». Отсюда берут начало термины abscissa, т. е. «отсеченная»,

ordinata и applicata, которые, впрочем, уко­ренились не сразу. Слово

«абсцисса», встречавшееся в смысле отрезка у различных авторов, например

Кавальерп (1635), становится техниче­ским термином координатной геометрии в

1668 г. у Микеланджело Риччи (1619—1692) ii особенно у Лейбница, начиная с

рукописей 1673 г. Ферма и Декарт в своих основоположных сочинениях по

аналитической геомет­рии (1636—1637; писали еще об «отрезках диаметра». Слово

«ордината» в нашем смысле применял другой переводчик па латынь «Конических

се­чений» — Франчсско Мавролико. Ферма пользовался термином applica­ta, Декарт

— appliquee par ordre, т. е. французским переводом ordinatim applicata, но

также (в письме 1638 г.) словом ordonnee, которое неза­долго перед тем в 1637

г. употребил в своем курсе П. Эригон (в латин­ском тексте 1644г.—ordinata);

затем им стал регулярно пользоваться Лейбниц.

В середине XVIII в. слово «ордината» начинает вытеснять в геомет­рии на

плоскости слово «аппликата». Обе координаты первоначально назывались

неизвестными величинами, как у Ферма, или неопределенны­ми, как у Декарта;

слово «координаты» ввел в 1692 г. Лейбниц, имея в виду уже любые

криволинейные координаты. Но еще и позднее понятие о координатах связывалось

с отрезками диаметров и хордами плоских кривых. Так обстоит, например, дело в

статьях «Abscissa, die Abscisse» и «Ordinatae, ordinatim applicatae, die

Ordinaten» «Математического словаря» (Mathematisches Lexicon, Leipzig, 1716)

Xp. Вольфа (ср. стр. 35).

Термин «ось», который у Аполлония относился к взаимно перпендику­лярным

сопряженным диаметрам, употребил в более широком смысле И. Барроу (1670).

Обозначение начальной точки буквой О восходит к ее наименованию origine

— «начало», данному Ф. Лагиром в 1679 г.; два­дцатью годами ранее Я. де Витт

писал об initium immutabile, неподвижном начале. Декарт еще говорил о точке, с

которой начинаются вычисления. Вернемся от истории терминологии к истории

геометрических методов и идей.

Аналитическая геометрия Ферма

К разработке начал новой аналитической геометрии независимо друг от друга и

одновременно приступили оба крупнейших французских ма­тематика XVII в.— Ферма

и Декарт. Небольшое «Введение в изучение плоских и телесных мест» (Ad locos

pianos et solidos isagoge) Ферма было написано несколько ранее 1637 г., но

при жизни Ферма распространялось через Мерсепна и других только в рукописном

виде. Напомним, что «плоские и телесные места» — термины греческой геометрии

— означали прямые и окружности и соответственно эллипсы, параболы и

гиперболы. Работа написана в обозначениях Виета с соблюдением однородности

урав­нений.

Ферма формулирует принцип аналитической геометрии следующим образом: «Всякий

раз, когда в заключительном уравнении имеются две неизвестные величины

(quantitates ignotae), налицо имеется место, и ко­нец одной из них описывает

прямую или же кривую линию... Для уста­новления уравнений удобно расположить

обе неизвестные величины под некоторым заданным углом (который мы большей

частью принимаем прямым) и задать положение и конец одной из величин»

[3]. Как мы видим, под неизвестными величинами (координатами) Ферма понимает

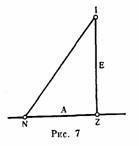
прямоли­нейные отрезки: первую из них он всякий раз обозначает NZ и

алгебра­ически буквой А, а вторую соответственно ZI и Е.

Затем по порядку рас­сматриваются различные плоские и телесные места.

Уравнение прямой, проходящей через начальную точку, Ферма вы­водит в форме

D на А равно В на Е,

т. е. dx = by (на рис. 7 нанесена лишь часть прямой NI, так как

Ферма пользуется положительными координатами). К этому случаю приводится общее

уравнение первой степени (с указанным ограничением) и несколько далее

однородное уравнение второй степени, причем здесь говорится лишь об одной из

двух возможных прямых. Первое приведение по существу со­стоит в преобразовании

координат, именно в параллельном сдвиге вдоль горизонтальной оси: от уравнения

вида с - dx = by Ферма переходит к d (r - х) = by

, где dr = с. Идею преобразования координат путем па­раллельного

переноса системы Ферма более отчетливо выражает в сле­дующих примерах:

установив сначала, что в прямоугольной системе уравнение окружности с центром в

начальной точке есть b2 - x2 = у

2, он правильно характеризует общее уравнение окружности и для образца

преобразует к основной форме уравнение

b2 - 2dx = у2 + 2rу.

Для этого он производит дополнение до квадрата

p1 - (х + d)2 = (у + r)2, где р2 = r2 + b2 + d2,

затем пишет снова x вместо x + d и y вместо у + r и получает

p2 - x2 = у2.

Следует заметить все же, что Ферма обходит молчанием вопрос об отрица­тельных

координатах, какими оказываются координаты центра (-d, -r) в

данной задаче (ибо d и r у него положительные). Разумеется,

построить центр для него не представляло труда и в этом случае.

Основные уравнения конических сечений представляют собой у Ферма

непосредственное выражение в терминах алгебры их свойств, известных по труду

Аполлоиня. Для параболы это уравнения x2 = dy и

симметричное у2 = dx, для эллипса (b2

- x2)/y2 = const (указывается, что в случае

непрямого координатного угла кривая будет эллипсом и при const = 1), для

гиперболы (b2 + x2)/y2 =

const. Любопытно, что на рисунке в по­следнем случае изображены обе ветви

гиперболы, хотя опять-таки об отрицательных координатах ничего не сказано.

Кроме того, приводится уравнение равносторонней гиперболы ху=с. Все это

распространяется на соответствующие уравнения, дополненные линейными членами.

Страницы: 1, 2