|
|
| Реферат: Решение задач с помощью ортогонального проектирования |
Через прямую АВ и точку P, лежащую на другой заданной прямой, уже проведена
плоскость α – это плоскость МАВ.
2. В плоскости МАВ через точку Р проведем прямую РК║АВ.
3. Строим плоскость β, определяемую прямыми PQ и РК.
Ясно, что так как точка Q – точка пересечения медиан треугольника МВС, то
прямая KQ пройдет через вершину С.
Таким образом, в сечении пирамиды плоскостью β получаем треугольник СКР.
Так как прямая АВ║РК, то прямая АВ параллельна плоскости СКР. Найдем
расстояние, например, от точки О –середины ребра АВ до плоскости СКР. Для
этого через точку О проведем плоскость γ , перпендикулярную какой-нибудь
прямой. Лежащей в плоскости СКР, например, прямой РК.
Так как прямая РК║АВ, то плоскость γ будет тогда перпендикулярна
и прямой АВ. Итак, в плоскости МАВ прямая ОМ перпендикулярна прямой АВ, и,
легко убедиться, в плоскости АВС прямая ОС перпендикулярна прямой АВ. Тогда
плоскость, определяемая пересекающимися прямыми ОМ и ОС, - это и есть
плоскость γ перпендикулярная прямой АВ, т. е. и прямой РК.
- Находим линию пересечения плоскостей СКР и γ – прямую CL.
Расстояние от точки О до прямой СL равно расстоянию между
скрещивающимися прямыми АВ и PQ. Найдем его как высоту прямоугольного
треугольника LCO. Если ОН – высота этого треугольника, то
ОН∙СL=OC∙OL, где из прямоугольного треугольника АВС находим
ОС=½АВ=½ а√2, из прямоугольного треугольника МАВ
OL=½OM=¼ a√2, и из прямоугольного треугольника LCO
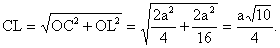 Таким образом, искомое расстояние ОН.
При решении задач на нахождение угла φ между скрещивающимися прямыми а и
b в общем случае можно поступить следующим образом:
1. Через одну из данных прямых, например через а, и через какую-нибудь
точку W, взятую на другой прямой, проведем плоскость α.
2. В плоскости α через точку W проведем затем прямую а1║а.
Угол между прямыми а1 и b равен искомому углу φ. (если
φ-угол между прямыми, 0 ≤ φ ≤ 90º.)
3. Выбрав на прямой а1 какую-нибудь точку К и на прямой b –
точку L, получим треугольник WKL. Если этот треугольник не прямоугольный, то,
подсчитав все его стороны, по теореме косинусов находим cos KWL. Понятно, что
если cos KWL>0, то угол острый, т.е. cos φ=cos KWL. Если же cos
KWL<0, то угол KWL тупой, т.е. φ=180º-KWL. Но cos(180º- KWL)=
- cos KWL. Таким образом, в этом случае cos φ= - cos KWL.
Задача 12. Все боковые грани призмы ABCA1B1C1
–квадраты. На ребрах АВ, A1C1, A1B1
и CС1 взяты соответственно точки P, Q, R, С2 – середины
этих ребер. Найти угол между прямыми PQ и С2R.
Решение (рис. 27). Выполним сначала необходимые дополнительные построения.
1. Через прямую С2R и точку Р, взятую на прямой PQ, проведем
плоскость α, в результате чего получим сечение призмы – четырехугольник
PRС1C.
2. В плоскости α через точку P проведем прямую PC3║ С
2R. Угол между прямыми PQ и PC3 равен искомому углу.
3. На прямой PQ возьмем точку Q, а на прямой PC3 – точку C3
и найдем cos QPC3.
Подсчитаем с этой целью стороны треугольника QPC3. Для выполнения
необходимых подсчетов пусть ребро призмы равно а.
В прямоугольном треугольнике PСC3 СР=½ а√3, СC3=С1С2=½ а.
В прямоугольном треугольнике QС1С3 С1Q=½ а, С1С3=½ 3а.
Таким образом, искомое расстояние ОН.
При решении задач на нахождение угла φ между скрещивающимися прямыми а и
b в общем случае можно поступить следующим образом:
1. Через одну из данных прямых, например через а, и через какую-нибудь
точку W, взятую на другой прямой, проведем плоскость α.
2. В плоскости α через точку W проведем затем прямую а1║а.
Угол между прямыми а1 и b равен искомому углу φ. (если
φ-угол между прямыми, 0 ≤ φ ≤ 90º.)
3. Выбрав на прямой а1 какую-нибудь точку К и на прямой b –
точку L, получим треугольник WKL. Если этот треугольник не прямоугольный, то,
подсчитав все его стороны, по теореме косинусов находим cos KWL. Понятно, что
если cos KWL>0, то угол острый, т.е. cos φ=cos KWL. Если же cos
KWL<0, то угол KWL тупой, т.е. φ=180º-KWL. Но cos(180º- KWL)=
- cos KWL. Таким образом, в этом случае cos φ= - cos KWL.
Задача 12. Все боковые грани призмы ABCA1B1C1
–квадраты. На ребрах АВ, A1C1, A1B1
и CС1 взяты соответственно точки P, Q, R, С2 – середины
этих ребер. Найти угол между прямыми PQ и С2R.
Решение (рис. 27). Выполним сначала необходимые дополнительные построения.
1. Через прямую С2R и точку Р, взятую на прямой PQ, проведем
плоскость α, в результате чего получим сечение призмы – четырехугольник
PRС1C.
2. В плоскости α через точку P проведем прямую PC3║ С
2R. Угол между прямыми PQ и PC3 равен искомому углу.
3. На прямой PQ возьмем точку Q, а на прямой PC3 – точку C3
и найдем cos QPC3.
Подсчитаем с этой целью стороны треугольника QPC3. Для выполнения
необходимых подсчетов пусть ребро призмы равно а.
В прямоугольном треугольнике PСC3 СР=½ а√3, СC3=С1С2=½ а.
В прямоугольном треугольнике QС1С3 С1Q=½ а, С1С3=½ 3а.
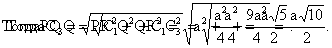 Соединим точку R с точкой Q. В прямоугольном треугольнике PQR PR=a,
QR=½ a.
Итак, в треугольнике PQС3 известны все стороны. Далее С3
Q²= =С3P²+PQ²-2 С3P·PQ cos QPC3,
Таким образом, угол QPC3 тупой, поэтому искомый угол
φ=180º- QPC3, и, значит, cos φ =cos(180º- QPC
3)= - сos QPC3.
При решении задач этого типа применяется либо поэтапно-вычислительный метод,
либо геометрический. Пусть в задаче требуется найти угол φ между прямой
АВ и плоскостью α. При решении задачи поэтапно-вычислительным методом
необходимо сначала построить проекцию прямой АВ на плоскость α. Для
этого следует из какой-нибудь точки прямой АВ опустить перпендикуляр на
плоскость α. Затем необходимо подсчитать какие-нибудь две стороны
полученного треугольника, в который входит угол φ, и найти какую-либо
тригонометрическую функцию угла φ, а потом и сам угол.
Задача 13. В правильной призме ABCA1B1C1 угол
между прямыми АB1 и A1С равен 2α. Найти угол между
прямой BC1 и плоскостью AСC1.
Решение (рис. 28). Выполним дополнительные построения. В плоскости ABB1
через точку A1 проведем прямую, параллельную прямой B1А, и
точку пересечения построенной прямой с прямой ВА обозначим D. Тогда угол DA
1C=2α. Соединим точку D с точкой С и проведем в треугольнике A1
CD медиану A1К. Так как заданная призма – правильная, то ее боковые
грани – равные прямоугольники, и, следовательно, B1А=A1C.
Кроме того, B1А=A1D. Тогда и A1D=A1
C, т. е. в треугольнике A1CD A1К┴СD. Проведем далее
в равностороннем треугольнике АВС медиану ВМ. Тогда ВМ┴АС. Но ясно и то,
что прямая A1А перпендикулярна плоскости АВС, т. е. A1
А┴ВМ, или, наоборот, ВМ ┴ A1А. Так как прямая ВМ
перпендикулярна двум пересекающимся прямым плоскости AСС1, и,
значит, соединив точку М с точкой С1, получим прямую С1М
– проекцию прямой ВС1 на плоскость AСС1 и прямоугольный
треугольник С1ВМ, угол ВС1М которого является углом между
прямой ВС1 и плоскостью АСС1.
Соединим точку R с точкой Q. В прямоугольном треугольнике PQR PR=a,
QR=½ a.
Итак, в треугольнике PQС3 известны все стороны. Далее С3
Q²= =С3P²+PQ²-2 С3P·PQ cos QPC3,
Таким образом, угол QPC3 тупой, поэтому искомый угол
φ=180º- QPC3, и, значит, cos φ =cos(180º- QPC
3)= - сos QPC3.
При решении задач этого типа применяется либо поэтапно-вычислительный метод,
либо геометрический. Пусть в задаче требуется найти угол φ между прямой
АВ и плоскостью α. При решении задачи поэтапно-вычислительным методом
необходимо сначала построить проекцию прямой АВ на плоскость α. Для
этого следует из какой-нибудь точки прямой АВ опустить перпендикуляр на
плоскость α. Затем необходимо подсчитать какие-нибудь две стороны
полученного треугольника, в который входит угол φ, и найти какую-либо
тригонометрическую функцию угла φ, а потом и сам угол.
Задача 13. В правильной призме ABCA1B1C1 угол
между прямыми АB1 и A1С равен 2α. Найти угол между
прямой BC1 и плоскостью AСC1.
Решение (рис. 28). Выполним дополнительные построения. В плоскости ABB1
через точку A1 проведем прямую, параллельную прямой B1А, и
точку пересечения построенной прямой с прямой ВА обозначим D. Тогда угол DA
1C=2α. Соединим точку D с точкой С и проведем в треугольнике A1
CD медиану A1К. Так как заданная призма – правильная, то ее боковые
грани – равные прямоугольники, и, следовательно, B1А=A1C.
Кроме того, B1А=A1D. Тогда и A1D=A1
C, т. е. в треугольнике A1CD A1К┴СD. Проведем далее
в равностороннем треугольнике АВС медиану ВМ. Тогда ВМ┴АС. Но ясно и то,
что прямая A1А перпендикулярна плоскости АВС, т. е. A1
А┴ВМ, или, наоборот, ВМ ┴ A1А. Так как прямая ВМ
перпендикулярна двум пересекающимся прямым плоскости AСС1, и,
значит, соединив точку М с точкой С1, получим прямую С1М
– проекцию прямой ВС1 на плоскость AСС1 и прямоугольный
треугольник С1ВМ, угол ВС1М которого является углом между
прямой ВС1 и плоскостью АСС1.
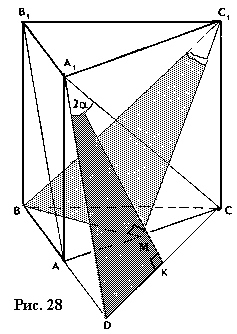 Рассмотрим прямоугольные треугольники С1ВМ и А1DK. У них С
1В=А1D, и так как в треугольнике АCD CD=АС√3, то
DK=½АС√3. Но и а треугольнике АВС ВМ=½АС√3. Таким
образом, ВМ=DK. Итак, прямоугольные треугольники С1ВМ и А1
DK равны (по гипотенузе и катету). Тогда углы ВС1М и DА1K
равны. Но ясно, что угол DА1K=α. Следовательно, и угол ВС1
М=α.
Пусть П1 и П2 – данные плоскости, пересекающиеся по прямой
АВ (рис. 29). Через некоторую точку F прямой АВ проведем в плоскости П1
прямую FC^AB, а в плоскости П2 прямую FD^AB. Плоскость CFD, таким
образом, перпендикулярна прямой АВ, и угол j между прямыми FC и FD является
углом между плоскостями П1 и П2 . По определению угла
между прямыми 0°<j£90°.
Одним из методов решения задач на нахождение угла между плоскостями является
поэтапно-вычислительный метод. Применение этого метода может опираться на
использование формулы
Рассмотрим прямоугольные треугольники С1ВМ и А1DK. У них С
1В=А1D, и так как в треугольнике АCD CD=АС√3, то
DK=½АС√3. Но и а треугольнике АВС ВМ=½АС√3. Таким
образом, ВМ=DK. Итак, прямоугольные треугольники С1ВМ и А1
DK равны (по гипотенузе и катету). Тогда углы ВС1М и DА1K
равны. Но ясно, что угол DА1K=α. Следовательно, и угол ВС1
М=α.
Пусть П1 и П2 – данные плоскости, пересекающиеся по прямой
АВ (рис. 29). Через некоторую точку F прямой АВ проведем в плоскости П1
прямую FC^AB, а в плоскости П2 прямую FD^AB. Плоскость CFD, таким
образом, перпендикулярна прямой АВ, и угол j между прямыми FC и FD является
углом между плоскостями П1 и П2 . По определению угла
между прямыми 0°<j£90°.
Одним из методов решения задач на нахождение угла между плоскостями является
поэтапно-вычислительный метод. Применение этого метода может опираться на
использование формулы 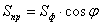 , где Sф-площадь фигуры F, лежащей в одной из плоскостей П1
или П2 , Sпр- площадь ортогональной проекции фигуры Ф на
другую плоскость из этих плоскостей, j - угол между плоскостями П1 и
П2 . В некоторых же случаях применение поэтапно-вычислительного
метода связано с необходимостью построения угла j между плоскостями и затем
треугольника, содержащего угол j или угол j1=180°-j. Подсчитывая
стороны этого треугольника, находят какую-либо тригонометрическую функцию угла
j (или угла j1), а затем и угол j.
Если рассматриваемый треугольник не является прямоугольным, то обычно находят
cos j (или cos j1). Если при этом cos j =m³0, то угол j - это
искомый угол и j=arcos m; если cos j =m<0, то искомым является угол j1
=180°--j. В этом случае угол cos j1=cos(180°--j)= -cos j , и,
следовательно, j1=arcos(-m).
, где Sф-площадь фигуры F, лежащей в одной из плоскостей П1
или П2 , Sпр- площадь ортогональной проекции фигуры Ф на
другую плоскость из этих плоскостей, j - угол между плоскостями П1 и
П2 . В некоторых же случаях применение поэтапно-вычислительного
метода связано с необходимостью построения угла j между плоскостями и затем
треугольника, содержащего угол j или угол j1=180°-j. Подсчитывая
стороны этого треугольника, находят какую-либо тригонометрическую функцию угла
j (или угла j1), а затем и угол j.
Если рассматриваемый треугольник не является прямоугольным, то обычно находят
cos j (или cos j1). Если при этом cos j =m³0, то угол j - это
искомый угол и j=arcos m; если cos j =m<0, то искомым является угол j1
=180°--j. В этом случае угол cos j1=cos(180°--j)= -cos j , и,
следовательно, j1=arcos(-m).
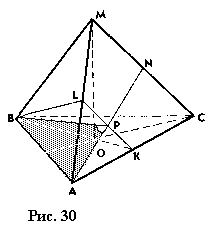
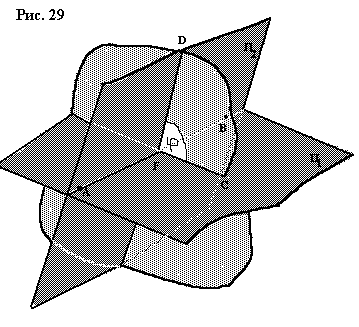 Задача 14. На ребрах АС и МА правильного тетраэдра МАВС взяты соответственно
точки К и L – середины этих ребер. Найти угол между плоскостями BLK и МАС.
Решение (рис. 30). Построим угол между плоскостями BLK и МАС. Для построения
перпендикуляра из точки В на прямую LK – линию пересечения плоскостей BLK и
МАС воспользуемся тем, что в треугольнике BLK BL=BK (как медианы
равносторонних треугольников). Тогда медиана ВР является перпендикуляром к
стороне LK. Так как в треугольнике ALK AL=AK, то медиана АР перпендикулярна
стороне LK. Таким образом, угол между прямыми ВР и АР – угол между
плоскостями BLK и МАС.
Пусть прямая АР пересекает ребро МС в точке N. Найдем угол ВРА треугольника ВРА.
Полагая для выполнения подсчетов ребро тетраэдра равным а, получаем
Задача 14. На ребрах АС и МА правильного тетраэдра МАВС взяты соответственно
точки К и L – середины этих ребер. Найти угол между плоскостями BLK и МАС.
Решение (рис. 30). Построим угол между плоскостями BLK и МАС. Для построения
перпендикуляра из точки В на прямую LK – линию пересечения плоскостей BLK и
МАС воспользуемся тем, что в треугольнике BLK BL=BK (как медианы
равносторонних треугольников). Тогда медиана ВР является перпендикуляром к
стороне LK. Так как в треугольнике ALK AL=AK, то медиана АР перпендикулярна
стороне LK. Таким образом, угол между прямыми ВР и АР – угол между
плоскостями BLK и МАС.
Пусть прямая АР пересекает ребро МС в точке N. Найдем угол ВРА треугольника ВРА.
Полагая для выполнения подсчетов ребро тетраэдра равным а, получаем 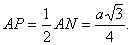 Из прямоугольного треугольника ВРК, в котором
Из прямоугольного треугольника ВРК, в котором 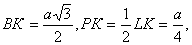 находим, что
находим, что
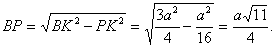 Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем
Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем 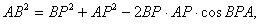 или
или
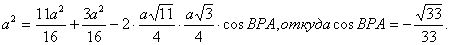
 Так как cos BPA<0. то ÐВРА – тупой. Таким образом, углом между прямыми ВР
и АР является угол j=180°-ÐВРА. Тогда cos j=cos (180° -ÐВРА)=--cos BPA=
Так как cos BPA<0. то ÐВРА – тупой. Таким образом, углом между прямыми ВР
и АР является угол j=180°-ÐВРА. Тогда cos j=cos (180° -ÐВРА)=--cos BPA=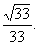 Итак, угол между плоскостями BLK и МАС – j=arccos
Итак, угол между плоскостями BLK и МАС – j=arccos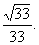 Если j - величина двугранного угла, то 0°<j<180°. При решении задач на
нахождение двугранного угла могут быть применены геометрический, а также
поэтапно-вычислительный методы. Применение поэтапно-вычислительного метода
связано необходимость построения линейного угла искомого двугранного угла j и с
построением треугольника, содержащего этот угол j или угол j1
=180°-j.Подсчитывая стороны построенного треугольника, находят угол j.
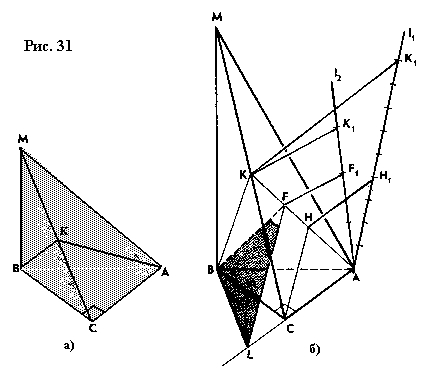
Задача 15. В основании пирамиды МАВС лежит прямоугольный треугольник. Боковое
ребро МВ перпендикулярно плоскости основания, и АС=ВС. На ребре МС взята
точка К – середина этого ребра. Найти двугранный угол ВКАС, если: а)МВ=АС;
б)МВ=2АС.
Решение а) (рис. 31, а). Геометрический метод. Так как прямая МВ
перпендикулярна плоскости АВС, то МВ^АС, т. е. И АС^МВ. Таким образом, АС^ВС и
АС^МВ, следовательно, АС^ВК, т. е. и ВК^АС (1).
Так как в треугольнике МВС МВ=ВС, то ВК не только медиана этого треугольника,
но и ВК^МС (2).
Из результатов (1) и (2) следует, что прямая ВК перпендикулярна плоскости
МАС. Тогда плоскость АВК, проходящая через прямую ВК, также перпендикулярна
плоскости МАС. Другими словами, двугранный угол ВАКС равен 90°.
б) (рис. 31, б) Поэтапно-вычислительный метод. Построим линейный угол
искомого двугранного угла, ребром которого является прямая АК, а гранями –
полуплоскости ВАК и САК.
1. В треугольнике АСК через вершину С проведем прямую, перпендикулярную
ребру АК искомого двугранного угла. Подсчитаем для этого все стороны
треугольника АСК, полагая, например, АС=а. Тогда ВС=а, МВ=2а
, МС=аÖ5, СК=½СМ=½Ö5, АК2=АС2
+СК2, т. е. АК=
Если j - величина двугранного угла, то 0°<j<180°. При решении задач на
нахождение двугранного угла могут быть применены геометрический, а также
поэтапно-вычислительный методы. Применение поэтапно-вычислительного метода
связано необходимость построения линейного угла искомого двугранного угла j и с
построением треугольника, содержащего этот угол j или угол j1
=180°-j.Подсчитывая стороны построенного треугольника, находят угол j.
Задача 15. В основании пирамиды МАВС лежит прямоугольный треугольник. Боковое
ребро МВ перпендикулярно плоскости основания, и АС=ВС. На ребре МС взята
точка К – середина этого ребра. Найти двугранный угол ВКАС, если: а)МВ=АС;
б)МВ=2АС.
Решение а) (рис. 31, а). Геометрический метод. Так как прямая МВ
перпендикулярна плоскости АВС, то МВ^АС, т. е. И АС^МВ. Таким образом, АС^ВС и
АС^МВ, следовательно, АС^ВК, т. е. и ВК^АС (1).
Так как в треугольнике МВС МВ=ВС, то ВК не только медиана этого треугольника,
но и ВК^МС (2).
Из результатов (1) и (2) следует, что прямая ВК перпендикулярна плоскости
МАС. Тогда плоскость АВК, проходящая через прямую ВК, также перпендикулярна
плоскости МАС. Другими словами, двугранный угол ВАКС равен 90°.
б) (рис. 31, б) Поэтапно-вычислительный метод. Построим линейный угол
искомого двугранного угла, ребром которого является прямая АК, а гранями –
полуплоскости ВАК и САК.
1. В треугольнике АСК через вершину С проведем прямую, перпендикулярную
ребру АК искомого двугранного угла. Подсчитаем для этого все стороны
треугольника АСК, полагая, например, АС=а. Тогда ВС=а, МВ=2а
, МС=аÖ5, СК=½СМ=½Ö5, АК2=АС2
+СК2, т. е. АК=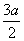 .
.
 Если СН^АК, то СН·АК=АС·СК, откуда СН=
Если СН^АК, то СН·АК=АС·СК, откуда СН=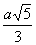 . Тогда АН=
. Тогда АН=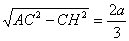 , и,
следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН,
которая перпендикулярна прямой АК.
2. В треугольнике АВК через вершину В проведем прямую, перпендикулярную
ребру АК двугранного угла ВАКС. Для этого подсчитаем стороны треугольника АВК.
Получаем АВ=аÖ2, ВК=½МС=½а√2 и АК= , и,
следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН,
которая перпендикулярна прямой АК.
2. В треугольнике АВК через вершину В проведем прямую, перпендикулярную
ребру АК двугранного угла ВАКС. Для этого подсчитаем стороны треугольника АВК.
Получаем АВ=аÖ2, ВК=½МС=½а√2 и АК=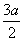 .
Если BF^АК, АВ2-AF2=ВК2-KF2, или 2
а2-AF2=
.
Если BF^АК, АВ2-AF2=ВК2-KF2, или 2
а2-AF2=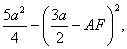 откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение
точки F и затем прямой BF, которая перпендикулярна прямой АК.
3. В треугольнике АСК через точку F проведем прямую FL║СН. Тогда
FL^АК. Так как, кроме того, BF^АК, то ÐBFL – линейный угол двугранного
угла ВАКС.
4. Соединим точку В с точкой L и подсчитаем стороны треугольника BFL. BF=
откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение
точки F и затем прямой BF, которая перпендикулярна прямой АК.
3. В треугольнике АСК через точку F проведем прямую FL║СН. Тогда
FL^АК. Так как, кроме того, BF^АК, то ÐBFL – линейный угол двугранного
угла ВАКС.
4. Соединим точку В с точкой L и подсчитаем стороны треугольника BFL. BF=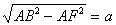 . Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a,
АН=
. Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a,
АН=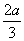 , СН= , СН=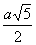 .
Тогда FL=
.
Тогда FL=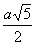 . Так как AL= . Так как AL=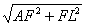 = =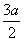 , то CL=AL – AC=½a. Тогда BL= , то CL=AL – AC=½a. Тогда BL=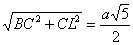 .
Итак, в треугольнике BFL известны все стороны: BF=a, FL= .
Итак, в треугольнике BFL известны все стороны: BF=a, FL=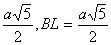 .
5. Из треугольника BFL по теореме косинусов получаем:
BL2=BF2+FL2-2BF·FL·cosBFL, или .
5. Из треугольника BFL по теореме косинусов получаем:
BL2=BF2+FL2-2BF·FL·cosBFL, или
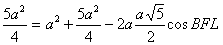 , откуда cosBFL= , откуда cosBFL=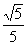 .
Это значит, что двугранный угол ВАКС равен arccos .
Это значит, что двугранный угол ВАКС равен arccos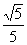 .
Итак, очевидна актуальность решения задач с помощью ортогонального
проектирования. В реферате рассмотрены разнообразные задания по стереометрии.
Показаны построения прямой и сечений на изображениях плоских и
пространственных фигур. Также даны решения по вычислению расстояний (между
точками, от точки до прямой, от точки до плоскости, между скрещивающимися
прямыми), нахождению углов (между скрещивающимися прямыми, между прямой и
плоскостью, меду плоскостями). При рассмотрении задач использовались
следующие способы и методы: способ выносных чертежей, вычислительный и
геометрический способы, поэтапно-вычислительный и координатный методы.
1. Василенко Е.А. Начертательная геометрия. – М., 1990..
2. Гордон В.О., Симинцев М.А., Агневских М.А. Курс начертательной
геометрии. – М.,1963.
3. Литвиненко В.Н. Сборник задач по стереометрии. – М., 1990..
4. Розов С.В. Сборник заданий. – М., 1988 .
Итак, очевидна актуальность решения задач с помощью ортогонального
проектирования. В реферате рассмотрены разнообразные задания по стереометрии.
Показаны построения прямой и сечений на изображениях плоских и
пространственных фигур. Также даны решения по вычислению расстояний (между
точками, от точки до прямой, от точки до плоскости, между скрещивающимися
прямыми), нахождению углов (между скрещивающимися прямыми, между прямой и
плоскостью, меду плоскостями). При рассмотрении задач использовались
следующие способы и методы: способ выносных чертежей, вычислительный и
геометрический способы, поэтапно-вычислительный и координатный методы.
1. Василенко Е.А. Начертательная геометрия. – М., 1990..
2. Гордон В.О., Симинцев М.А., Агневских М.А. Курс начертательной
геометрии. – М.,1963.
3. Литвиненко В.Н. Сборник задач по стереометрии. – М., 1990..
4. Розов С.В. Сборник заданий. – М., 1988
Страницы: 1, 2, 3, 4
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



