|
|
| Реферат: Теория флюксий |
|
/td> |
выражает искомое соотношение величин x и y.
Здесь следует заметить, что хотя член axy встречается дважды, я все же
не выписываю его дважды в сумме
но один из них отбрасываю как лишний. Таким образом, если какой-либо член
встречается дважды (или еще больше раз в том случае, если он получается от
различных флюэнт), то в сумме членов его следует выписывать лишь один раз.»
( Здесь описана следующая процедура нахождения частного решения
дифференциального уравнения
(3x2 2ax + ay)dx = (3y2 + ax)dy. |
|
Уравнение записывается в виде
d(x3 ax2 y 3 axy) = 0, |
|
откуда вытекает наличие решения
x3 ax2 y 3 axy = 0. |
|
Произвольной постоянной Ньютон не добавляет).
Далее Ньютон пишет: «Прочие необходимые замечания я оставляю на долю
проницательности самого мастера, тем более, что было бы излишним чересчур
долго останавливаться на этом предмете, так как этим приемом проблема может
быть решена не всегда. Я добавляю только одно замечание, а именно, что, найдя
таким методом зависимость между флюэнтами, ты можешь затем согласно проблеме
I вернуться к предложенному уравнению, содержащему флюксии, и тогда наверное
узнаешь, правильно ли произведено действие или нет.
Предпослав все это беглым образом, я приступаю к общему решению.
Подготовление к решению.
Прежде всего следует заметить, что в предложенном уравнении знаки флюксий в
отдельных членах должны быть одинакового измерения (ибо флюксии суть величины
иного рода, чем те, для которых они служат флюксиями)»
Речь идет о том, что уравнение должно быть однородным, т. е. все его слагаемые
должны измеряться в одних и тех же единицах измерения. Во времена Ньютона
выражение вида x2 + x считалось неправильным,
поскольку нельзя "складывать площадь и длину"
«Если в каком-либо случае дело обстоит иначе, то флюксию какой-либо флюэнты
следует принять за единицу и помножить на нее низшие члены столько раз, сколько
требуется для того, чтобы знаки флюксий привелись во всех членах к одинаковому
числу измерений. Уравнения, которые содержат только флюэнты, имеющие везде
одинаковое число измерений, всегда можно привести к такому виду, чтобы в одной
части находилось отношение флюксий (например, 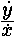 или
или 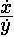 или или 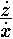 и т. д.), а в другой значение этого отношения, выраженное в простых
алгебраических членах (таким образом, левая часть уравнения будет зависеть от
производной y по x), как, например,
и т. д.), а в другой значение этого отношения, выраженное в простых
алгебраических членах (таким образом, левая часть уравнения будет зависеть от
производной y по x), как, например,
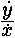 = 2 + 2x y. = 2 + 2x y.
|
|
В том случае, когда не может быть применено приведенное выше частное решение,
уравнения всегда следует представлять в этой форме.
Поэтому, когда в значении этого отношения имеется какой-либо член с составным
знаменателем или радикалом или когда это отношение представляет собой корень
неявного уравнения, то прежде чем приступить к действиям, ты должен совершить
приведение либо посредством деления, либо с помощью извлечения корня, либо с
помощью решения неявного уравнения, как мы это объясняли выше.»
Речь идет, по существу, о хорошо известном методе Ньютона решения нелинейных
уравнений, описываемом Ньютоном в предыдущем разделе трактата в форме
представления решений в виде ряда.
«Пусть, например, предложено уравнение
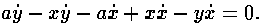 Прежде всего приведение его дает
Прежде всего приведение его дает 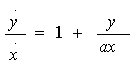 или
или 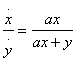 При первом предположении я обращаю выражение y/(a x
), у которого знаменатель есть составное выражение a x,
в бесконечный ряд простых членов:
При первом предположении я обращаю выражение y/(a x
), у которого знаменатель есть составное выражение a x,
в бесконечный ряд простых членов: 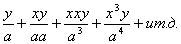 (приведение это производятся делением числителя y на знаменатель a
x), откуда получаю
(приведение это производятся делением числителя y на знаменатель a
x), откуда получаю 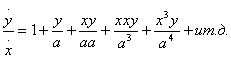 с помощью чего и следует определить отношение между x и y.
Таким же образом, если данное уравнение есть
с помощью чего и следует определить отношение между x и y.
Таким же образом, если данное уравнение есть
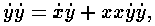 или
или
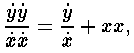 или после дальнейшего преобразования
или после дальнейшего преобразования
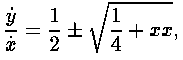 то я извлекаю квадратный корень из членов 1/4+xx и получаю бесконечный ряд
то я извлекаю квадратный корень из членов 1/4+xx и получаю бесконечный ряд
| 1 2 | + xx x4 + 2x7 5x8 + 14x10 и т. д. |
|
При подстановке его вместо 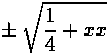 я буду иметь я буду иметь
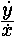 = 1 + xx x4+2x7 5x8 + 14x10 и т. д. = 1 + xx x4+2x7 5x8 + 14x10 и т. д.
|
|
или
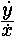 = xx + x4 2x7 + 5x8 14x10 и т. д., = xx + x4 2x7 + 5x8 14x10 и т. д.,
|
|
смотря по тому, прибавляю ли 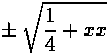 к 1/2 или вычитаю из нее.»
В этих примерах Ньютон описывает первый этап своего метод решения
дифференциальных уравнений. В современной терминологии это приведение
уравнения к нормальной форме и разложение правой части в степенной ряд.
«Далее, чтобы легче было отличать одну из флюэнт от других, можно с
достаточным основанием ту из флюксий, которая находится в числителе
отношения, назвать величиной отнесенной, а ту, которая стоит в знаменателе и
с которой сравнивается первая, соотнесенной, -зависимая и, соответственно,
независимая переменные в дифференциальном уравнении; и этими же терминами
можно соответственно называть и флюэнты. Для лучшего понимания дальнейшего
можно представлять себе, что соотнесенная величина есть время или, лучше,
какая-либо равномерно текущая величина, с помощью которой выражается и
измеряется время, а другая, именно отнесенная, величина есть пространство,
проходимое за это время вещью или точкой, обладающей некоторым ускоренным или
замедленным движением. Сущность проблемы заключается тогда в определении
пройденного за все время пути, если известна скорость для любого момента
времени.» к 1/2 или вычитаю из нее.»
В этих примерах Ньютон описывает первый этап своего метод решения
дифференциальных уравнений. В современной терминологии это приведение
уравнения к нормальной форме и разложение правой части в степенной ряд.
«Далее, чтобы легче было отличать одну из флюэнт от других, можно с
достаточным основанием ту из флюксий, которая находится в числителе
отношения, назвать величиной отнесенной, а ту, которая стоит в знаменателе и
с которой сравнивается первая, соотнесенной, -зависимая и, соответственно,
независимая переменные в дифференциальном уравнении; и этими же терминами
можно соответственно называть и флюэнты. Для лучшего понимания дальнейшего
можно представлять себе, что соотнесенная величина есть время или, лучше,
какая-либо равномерно текущая величина, с помощью которой выражается и
измеряется время, а другая, именно отнесенная, величина есть пространство,
проходимое за это время вещью или точкой, обладающей некоторым ускоренным или
замедленным движением. Сущность проблемы заключается тогда в определении
пройденного за все время пути, если известна скорость для любого момента
времени.»
Классификация уравнений в рамках проблемы и их решение
Уравнения, относящиеся к этой проблеме, Ньютон разделил на три рода:
1. уравнения вида F(x,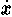 ,
,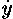 ) = 0, приводящиеся к виду
f(x,dy/dx) = 0 «.те уравнения, в которых имеются две
флюксии величин и только одна из флюэнт».
2. уравнения вида F(x,y, ) = 0, приводящиеся к виду
f(x,dy/dx) = 0 «.те уравнения, в которых имеются две
флюксии величин и только одна из флюэнт».
2. уравнения вида F(x,y,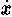 ,
,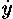 ) = 0, приводящиеся к виду
f(x, y, dy/dx) = 0. «.те, которые содержат обе
текущие величины с их флюксиями.»
3. Одно дифференциальное уравнение с несколькими неизвестными. «.те, в
которых имеются флюксии больше чем двух величин»
Ньютон рассматривает и решение каждого из случаев. ) = 0, приводящиеся к виду
f(x, y, dy/dx) = 0. «.те, которые содержат обе
текущие величины с их флюксиями.»
3. Одно дифференциальное уравнение с несколькими неизвестными. «.те, в
которых имеются флюксии больше чем двух величин»
Ньютон рассматривает и решение каждого из случаев.
Решение первого случая.
«Прими единственную имеющуюся в уравнению флюэнту за соотнесенную величину и,
преобразовав уравнение в соответствии с этим допущением (т. е. установив
отношение флюксии второй величины к флюксии первой и значение этого
отношения, выраженного через простые члены (Т. е. разложенного в степенной
ряд)), помножь значение отношения флюксий на соотнесенную величину. Затем
раздели каждый член этого выражения на показатель степени, в которую
возведена в нем соотнесенная величина; то что ты таким образом получишь, и
будет равно другой текущей величине.»
В современных терминах это выглядит так: нужно уравнение f(x,
y) = 0 привести к виду y’= j (x) и проинтегрировать.
Процедура же интегрирования сводится к разложению j в степенной ряд и
последующему почленному интегрированию ряда.
Решение второго случая.
«До сих пор речь шла об уравнениях, которые заключают одну флюэнту. Когда же
в уравнении появляются обе, то уравнение прежде всего следует привести к уже
указанному виду, полагая с одной стороны отношение флюксий, а с другой
равную ему сумму простых членов.
Кроме того, если какой-либо член преобразованного таким образом уравнения
представляет дробь с флюэнтой в знаменателе, то он должен быть освобожден от
подобного знаменателя при помощи вышеприведенной замены текущей величины.
Таким образом, если дано уравнение
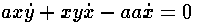 или
или 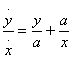 то в силу наличия члена a/x я беру
произвольное b и вместо x пишу b + x или b
- x или x- b. Если написать b +
x, то получается
то в силу наличия члена a/x я беру
произвольное b и вместо x пишу b + x или b
- x или x- b. Если написать b +
x, то получается 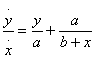 Обращая затем при помощи деления член a/(b + x) в
бесконечный ряд, я вывел бы, что
Обращая затем при помощи деления член a/(b + x) в
бесконечный ряд, я вывел бы, что 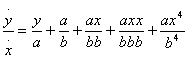 и т.д.
Правило: Подготовив таким образом (если это нужно) уравнение, расположи
члены по степеням флюэнт, сперва ставя те, которые не содержат отнесенной
величины, затем те, которые содержат ее в наименьшей степени, и т. д. Таким же
образом распредели по отдельным родам члены согласно степеням соотнесенной
величины и члены, которые образуют первый род (именно, которые не содержат
отнесенной величины), запиши в виде горизонтального ряда слева направо, а
остальные выпиши в левом столбце так, чтобы они образовывали нисходящий ряд,
как это показано в нижеприведенной таблице.
Приготовив таким образом ряды, помножь первый или низший член первого рода на
соотнесенную величину и раздели произведение на показатель его степени и то,
что при этом получится, введи в результат (Предлагается проинтегрировать ряд
по степеням независимой переменной).Затем подставь это значение вместо
отнесенной величины в те члены уравнения, которые расположены в левом
столбце; второй член результата ты получишь из следующего низшего члена по
тому же способу, каким добыт первый член результата. Повторяя эти действия,
ты можешь продолжить результат сколь угодно»
По существу, здесь предлагается конечный алгоритм следующих действий:
1. В уравнение подставляется разложение решения в ряд по степеням
независимого аргумента с неопределенными коэффициентами.
2. Коэффициенты при одинаковых степенях приравниваются.
3. Получившаяся (бесконечная) система алгебраических уравнений
получается треугольной, поэтому можно выписать ее решение в явном виде).
Это станет еще ясней из рассмотрения нескольких примеров.
Пример 3.
Пусть дано уравнение
и т.д.
Правило: Подготовив таким образом (если это нужно) уравнение, расположи
члены по степеням флюэнт, сперва ставя те, которые не содержат отнесенной
величины, затем те, которые содержат ее в наименьшей степени, и т. д. Таким же
образом распредели по отдельным родам члены согласно степеням соотнесенной
величины и члены, которые образуют первый род (именно, которые не содержат
отнесенной величины), запиши в виде горизонтального ряда слева направо, а
остальные выпиши в левом столбце так, чтобы они образовывали нисходящий ряд,
как это показано в нижеприведенной таблице.
Приготовив таким образом ряды, помножь первый или низший член первого рода на
соотнесенную величину и раздели произведение на показатель его степени и то,
что при этом получится, введи в результат (Предлагается проинтегрировать ряд
по степеням независимой переменной).Затем подставь это значение вместо
отнесенной величины в те члены уравнения, которые расположены в левом
столбце; второй член результата ты получишь из следующего низшего члена по
тому же способу, каким добыт первый член результата. Повторяя эти действия,
ты можешь продолжить результат сколь угодно»
По существу, здесь предлагается конечный алгоритм следующих действий:
1. В уравнение подставляется разложение решения в ряд по степеням
независимого аргумента с неопределенными коэффициентами.
2. Коэффициенты при одинаковых степенях приравниваются.
3. Получившаяся (бесконечная) система алгебраических уравнений
получается треугольной, поэтому можно выписать ее решение в явном виде).
Это станет еще ясней из рассмотрения нескольких примеров.
Пример 3.
Пусть дано уравнение
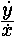 = 1 3x + y + xx + = 1 3x + y + xx + 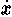 y. y.
|
|
Члены его 1 3x + xx, не содержащие отнесенной величины
y, расположены, как видишь, в первой строке, а остальные члены y и
xy в левом столбце.
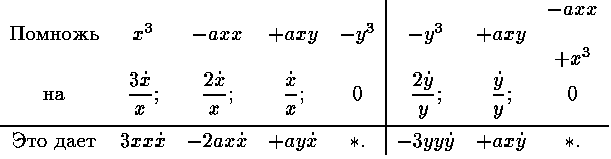 Пример 4.
Точно так же, если требуется определить соотношение между x и y из уравнения
Пример 4.
Точно так же, если требуется определить соотношение между x и y из уравнения 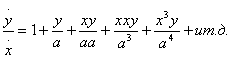 в котором ряд предполагается продолжающимся до бесконечности, то наверху я
пишу 1, остальные члены выписываю в левом столбце и затем произвожу действие,
как это видно из представленной таблицы.
в котором ряд предполагается продолжающимся до бесконечности, то наверху я
пишу 1, остальные члены выписываю в левом столбце и затем произвожу действие,
как это видно из представленной таблицы.
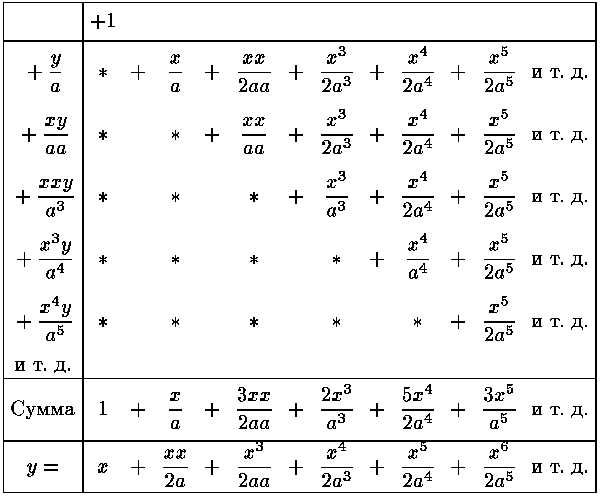 Предполагая, что мне предложено было найти выражение для y лишь до
шестой степени x, я в силу этого опускаю при действии все члены,
которые, как я предвижу, не будут использованы; это отмечается знаком "и т.
д.", который я ставлю вместо отсеченных частей рядов»
Приведенные выше сведения были частично взяты из перевода работы "Метод
флюксий и бесконечных рядов с приложением его к геометрии кривых", которая
была написана Ньютоном в 1664-71 гг. и издана уже после его смерти.
Метод флюксий применяется здесь к большому числу геометрических вопросов
(задачи на касательные, кривизну, экстремумы, квадратуры, спрямления и др.);
здесь же выражается в элементарных функциях ряд интегралов от функций,
содержащих квадратный корень из квадратичного трёхчлена. Большое внимание
уделено в "Методе флюксий" интегрированию обыкновенных дифференциальных
уравнений, причём основную роль играет представление решения в виде
бесконечного степенного ряда.
Во введении к "Рассуждению о квадратуре кривых" (основной текст 1665-66,
введение и окончательный вариант 1670, опубликован 1704) и в "Началах" он
намечает программу построения метода флюксий на основе учения о пределе, о
"последних отношениях исчезающих величин" или "первых отношениях
зарождающихся величин", не давая, впрочем, формального определения предела и
рассматривая его как первоначальное.
В сочинении "Анализ при помощи уравнений с бесконечным числом членов" (1669,
опубликовано 1711) Ньютон вычислил производную и интеграл любой степенной
функции. Различные рациональные, дробно-рациональные, иррациональные и
некоторые трансцендентные функции (логарифмическую, показательную, синус,
косинус, арксинус) Ньютон выражал с помощью бесконечных степенных рядов.
Предполагая, что мне предложено было найти выражение для y лишь до
шестой степени x, я в силу этого опускаю при действии все члены,
которые, как я предвижу, не будут использованы; это отмечается знаком "и т.
д.", который я ставлю вместо отсеченных частей рядов»
Приведенные выше сведения были частично взяты из перевода работы "Метод
флюксий и бесконечных рядов с приложением его к геометрии кривых", которая
была написана Ньютоном в 1664-71 гг. и издана уже после его смерти.
Метод флюксий применяется здесь к большому числу геометрических вопросов
(задачи на касательные, кривизну, экстремумы, квадратуры, спрямления и др.);
здесь же выражается в элементарных функциях ряд интегралов от функций,
содержащих квадратный корень из квадратичного трёхчлена. Большое внимание
уделено в "Методе флюксий" интегрированию обыкновенных дифференциальных
уравнений, причём основную роль играет представление решения в виде
бесконечного степенного ряда.
Во введении к "Рассуждению о квадратуре кривых" (основной текст 1665-66,
введение и окончательный вариант 1670, опубликован 1704) и в "Началах" он
намечает программу построения метода флюксий на основе учения о пределе, о
"последних отношениях исчезающих величин" или "первых отношениях
зарождающихся величин", не давая, впрочем, формального определения предела и
рассматривая его как первоначальное.
В сочинении "Анализ при помощи уравнений с бесконечным числом членов" (1669,
опубликовано 1711) Ньютон вычислил производную и интеграл любой степенной
функции. Различные рациональные, дробно-рациональные, иррациональные и
некоторые трансцендентные функции (логарифмическую, показательную, синус,
косинус, арксинус) Ньютон выражал с помощью бесконечных степенных рядов.
Заключение
Таким образом, разработанная сначала Ньютоном, затем Лейбницем теория флюксий
дала начало дифференциальному и интегральному исчислениям в том виде, в
котором мы их знаем сегодня.
Литература:
1. Вавилов С. И., Исаак Ньютон, М., 1961;
2. Философия и история математики. Колмогоров А. Н., Математика, в книге:
Большая Советская энциклопедия, 2 изд., т. 26, М., 1954;
3. Математика, её содержание, методы и значение, т. 1-3, М., 1956;
4. Юшкевич А. П., История математики в средние века, М., 1961;
5. Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959;
6. Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М.,
1965;
7. Исаак Ньютон. Математические работы, ОНТИ, М.-Л., 1937
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|




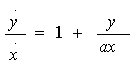 или
или 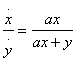 При первом предположении я обращаю выражение y/(a x
), у которого знаменатель есть составное выражение a x,
в бесконечный ряд простых членов:
При первом предположении я обращаю выражение y/(a x
), у которого знаменатель есть составное выражение a x,
в бесконечный ряд простых членов: 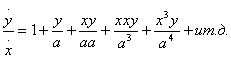 с помощью чего и следует определить отношение между x и y.
Таким же образом, если данное уравнение есть
с помощью чего и следует определить отношение между x и y.
Таким же образом, если данное уравнение есть
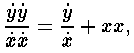 или после дальнейшего преобразования
или после дальнейшего преобразования
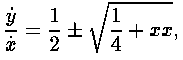 то я извлекаю квадратный корень из членов 1/4+xx и получаю бесконечный ряд
то я извлекаю квадратный корень из членов 1/4+xx и получаю бесконечный ряд
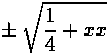 я буду иметь
я буду иметь
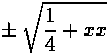 к 1/2 или вычитаю из нее.»
В этих примерах Ньютон описывает первый этап своего метод решения
дифференциальных уравнений. В современной терминологии это приведение
уравнения к нормальной форме и разложение правой части в степенной ряд.
«Далее, чтобы легче было отличать одну из флюэнт от других, можно с
достаточным основанием ту из флюксий, которая находится в числителе
отношения, назвать величиной отнесенной, а ту, которая стоит в знаменателе и
с которой сравнивается первая, соотнесенной, -зависимая и, соответственно,
независимая переменные в дифференциальном уравнении; и этими же терминами
можно соответственно называть и флюэнты. Для лучшего понимания дальнейшего
можно представлять себе, что соотнесенная величина есть время или, лучше,
какая-либо равномерно текущая величина, с помощью которой выражается и
измеряется время, а другая, именно отнесенная, величина есть пространство,
проходимое за это время вещью или точкой, обладающей некоторым ускоренным или
замедленным движением. Сущность проблемы заключается тогда в определении
пройденного за все время пути, если известна скорость для любого момента
времени.»
к 1/2 или вычитаю из нее.»
В этих примерах Ньютон описывает первый этап своего метод решения
дифференциальных уравнений. В современной терминологии это приведение
уравнения к нормальной форме и разложение правой части в степенной ряд.
«Далее, чтобы легче было отличать одну из флюэнт от других, можно с
достаточным основанием ту из флюксий, которая находится в числителе
отношения, назвать величиной отнесенной, а ту, которая стоит в знаменателе и
с которой сравнивается первая, соотнесенной, -зависимая и, соответственно,
независимая переменные в дифференциальном уравнении; и этими же терминами
можно соответственно называть и флюэнты. Для лучшего понимания дальнейшего
можно представлять себе, что соотнесенная величина есть время или, лучше,
какая-либо равномерно текущая величина, с помощью которой выражается и
измеряется время, а другая, именно отнесенная, величина есть пространство,
проходимое за это время вещью или точкой, обладающей некоторым ускоренным или
замедленным движением. Сущность проблемы заключается тогда в определении
пройденного за все время пути, если известна скорость для любого момента
времени.»
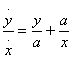 то в силу наличия члена a/x я беру
произвольное b и вместо x пишу b + x или b
- x или x- b. Если написать b +
x, то получается
то в силу наличия члена a/x я беру
произвольное b и вместо x пишу b + x или b
- x или x- b. Если написать b +
x, то получается 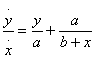 Обращая затем при помощи деления член a/(b + x) в
бесконечный ряд, я вывел бы, что
Обращая затем при помощи деления член a/(b + x) в
бесконечный ряд, я вывел бы, что 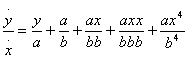 и т.д.
Правило: Подготовив таким образом (если это нужно) уравнение, расположи
члены по степеням флюэнт, сперва ставя те, которые не содержат отнесенной
величины, затем те, которые содержат ее в наименьшей степени, и т. д. Таким же
образом распредели по отдельным родам члены согласно степеням соотнесенной
величины и члены, которые образуют первый род (именно, которые не содержат
отнесенной величины), запиши в виде горизонтального ряда слева направо, а
остальные выпиши в левом столбце так, чтобы они образовывали нисходящий ряд,
как это показано в нижеприведенной таблице.
Приготовив таким образом ряды, помножь первый или низший член первого рода на
соотнесенную величину и раздели произведение на показатель его степени и то,
что при этом получится, введи в результат (Предлагается проинтегрировать ряд
по степеням независимой переменной).Затем подставь это значение вместо
отнесенной величины в те члены уравнения, которые расположены в левом
столбце; второй член результата ты получишь из следующего низшего члена по
тому же способу, каким добыт первый член результата. Повторяя эти действия,
ты можешь продолжить результат сколь угодно»
По существу, здесь предлагается конечный алгоритм следующих действий:
1. В уравнение подставляется разложение решения в ряд по степеням
независимого аргумента с неопределенными коэффициентами.
2. Коэффициенты при одинаковых степенях приравниваются.
3. Получившаяся (бесконечная) система алгебраических уравнений
получается треугольной, поэтому можно выписать ее решение в явном виде).
Это станет еще ясней из рассмотрения нескольких примеров.
Пример 3.
Пусть дано уравнение
и т.д.
Правило: Подготовив таким образом (если это нужно) уравнение, расположи
члены по степеням флюэнт, сперва ставя те, которые не содержат отнесенной
величины, затем те, которые содержат ее в наименьшей степени, и т. д. Таким же
образом распредели по отдельным родам члены согласно степеням соотнесенной
величины и члены, которые образуют первый род (именно, которые не содержат
отнесенной величины), запиши в виде горизонтального ряда слева направо, а
остальные выпиши в левом столбце так, чтобы они образовывали нисходящий ряд,
как это показано в нижеприведенной таблице.
Приготовив таким образом ряды, помножь первый или низший член первого рода на
соотнесенную величину и раздели произведение на показатель его степени и то,
что при этом получится, введи в результат (Предлагается проинтегрировать ряд
по степеням независимой переменной).Затем подставь это значение вместо
отнесенной величины в те члены уравнения, которые расположены в левом
столбце; второй член результата ты получишь из следующего низшего члена по
тому же способу, каким добыт первый член результата. Повторяя эти действия,
ты можешь продолжить результат сколь угодно»
По существу, здесь предлагается конечный алгоритм следующих действий:
1. В уравнение подставляется разложение решения в ряд по степеням
независимого аргумента с неопределенными коэффициентами.
2. Коэффициенты при одинаковых степенях приравниваются.
3. Получившаяся (бесконечная) система алгебраических уравнений
получается треугольной, поэтому можно выписать ее решение в явном виде).
Это станет еще ясней из рассмотрения нескольких примеров.
Пример 3.
Пусть дано уравнение
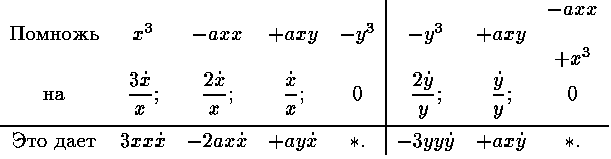 Пример 4.
Точно так же, если требуется определить соотношение между x и y из уравнения
Пример 4.
Точно так же, если требуется определить соотношение между x и y из уравнения 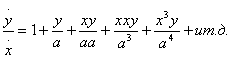 в котором ряд предполагается продолжающимся до бесконечности, то наверху я
пишу 1, остальные члены выписываю в левом столбце и затем произвожу действие,
как это видно из представленной таблицы.
в котором ряд предполагается продолжающимся до бесконечности, то наверху я
пишу 1, остальные члены выписываю в левом столбце и затем произвожу действие,
как это видно из представленной таблицы.
 Предполагая, что мне предложено было найти выражение для y лишь до
шестой степени x, я в силу этого опускаю при действии все члены,
которые, как я предвижу, не будут использованы; это отмечается знаком "и т.
д.", который я ставлю вместо отсеченных частей рядов»
Приведенные выше сведения были частично взяты из перевода работы "Метод
флюксий и бесконечных рядов с приложением его к геометрии кривых", которая
была написана Ньютоном в 1664-71 гг. и издана уже после его смерти.
Метод флюксий применяется здесь к большому числу геометрических вопросов
(задачи на касательные, кривизну, экстремумы, квадратуры, спрямления и др.);
здесь же выражается в элементарных функциях ряд интегралов от функций,
содержащих квадратный корень из квадратичного трёхчлена. Большое внимание
уделено в "Методе флюксий" интегрированию обыкновенных дифференциальных
уравнений, причём основную роль играет представление решения в виде
бесконечного степенного ряда.
Во введении к "Рассуждению о квадратуре кривых" (основной текст 1665-66,
введение и окончательный вариант 1670, опубликован 1704) и в "Началах" он
намечает программу построения метода флюксий на основе учения о пределе, о
"последних отношениях исчезающих величин" или "первых отношениях
зарождающихся величин", не давая, впрочем, формального определения предела и
рассматривая его как первоначальное.
В сочинении "Анализ при помощи уравнений с бесконечным числом членов" (1669,
опубликовано 1711) Ньютон вычислил производную и интеграл любой степенной
функции. Различные рациональные, дробно-рациональные, иррациональные и
некоторые трансцендентные функции (логарифмическую, показательную, синус,
косинус, арксинус) Ньютон выражал с помощью бесконечных степенных рядов.
Предполагая, что мне предложено было найти выражение для y лишь до
шестой степени x, я в силу этого опускаю при действии все члены,
которые, как я предвижу, не будут использованы; это отмечается знаком "и т.
д.", который я ставлю вместо отсеченных частей рядов»
Приведенные выше сведения были частично взяты из перевода работы "Метод
флюксий и бесконечных рядов с приложением его к геометрии кривых", которая
была написана Ньютоном в 1664-71 гг. и издана уже после его смерти.
Метод флюксий применяется здесь к большому числу геометрических вопросов
(задачи на касательные, кривизну, экстремумы, квадратуры, спрямления и др.);
здесь же выражается в элементарных функциях ряд интегралов от функций,
содержащих квадратный корень из квадратичного трёхчлена. Большое внимание
уделено в "Методе флюксий" интегрированию обыкновенных дифференциальных
уравнений, причём основную роль играет представление решения в виде
бесконечного степенного ряда.
Во введении к "Рассуждению о квадратуре кривых" (основной текст 1665-66,
введение и окончательный вариант 1670, опубликован 1704) и в "Началах" он
намечает программу построения метода флюксий на основе учения о пределе, о
"последних отношениях исчезающих величин" или "первых отношениях
зарождающихся величин", не давая, впрочем, формального определения предела и
рассматривая его как первоначальное.
В сочинении "Анализ при помощи уравнений с бесконечным числом членов" (1669,
опубликовано 1711) Ньютон вычислил производную и интеграл любой степенной
функции. Различные рациональные, дробно-рациональные, иррациональные и
некоторые трансцендентные функции (логарифмическую, показательную, синус,
косинус, арксинус) Ньютон выражал с помощью бесконечных степенных рядов.