Шпора: Шпора алгебра (институт)
1. Определитель это число соответствующее данной квадратной матрице и
вычисленное определённым образом. detA=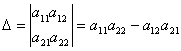
. Определитель можно подсчитать 2 способами. Правило треугольников и правило
дописывания элементов.
Правило треугольников.
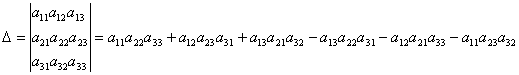
Правило дописывания элементов
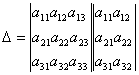 = = 
2 Свойства определителя. а) Если строка или столбец в определители
состоит из нулей, то определитель равен 0. б) Если в определители две
одинаковые строки (столбцы) то d=0 в) Общий множитель строки столбца можно
вынести за скобку г) d не измениться, если к элементам соответствующей строки
добавить соответствующие элементы другой строки или столба умноженное на одно
и тоже число. Д). Если в определителе какая – либо строка (столбец)
может быть представлен в виде двух слагаемых то самоопределитель может быть
представлен в виде суммы двух определителей в которых все элементы такие же
как в исходном определителе кроме указанной строки (столбца). В первом
определителе стоят первые слагаемые во втором вторые. З). Если в
определителе поменять местами две строки (столбца), то определитель изменит
знак на противоположный. Е). Если в определителе две строки (столбца)
пропорциональны то он равен 0. к). При транспонирование значение
определителя не меняется. Транспонирование – это замена строк столбцами и
наоборот.
3. Минором элемента 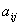
называется d полученный из исходного вычеркиванием i строки и j столбца. 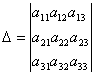 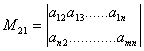
Алгебраическое дополнением элемента 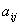
называется его минор взятый с определённым знаком. 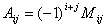
4.Для вычислений d порядка>3 используется: любой d может быть
представлен как сумма произведений элементов какой либо строки (столбца) на их
алгебраическое дополнение. Также есть правило треугольников и правило
дописывания элементов.
5. Таблица чисел состоящая из m строк и n столбцов называется
матрицей. A1*x1+A2*x2=b1 расширенная | a1 a2 b1|
6 Правило Крамара (если система неоднородна, т.е. свобдые члены не равны
и не равны 0): если d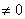
то система имеет одно единственное решение, которое можно найти по формулам
Крамара 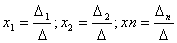 . В этих . В этих
формулах 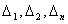 это это
определители, полученные из основного определителя заменой соответствующего
столбца на столбец свободных членов. Основной определитель системы равен 0, а
хотя бы один из определителей 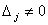
то система не имеет решений. Определитель равен 0 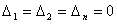
, бесконечное множество решений.
7 Система однородных линейных уравнений имеет единственное нулевое решение когда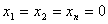
8 Однородная система линейных уравнений имеет ненулевое решение, если
основной определитель системы равен 0
9 Метод Гаусса Нужно смотреть всегда, не пришла ли система к виду
0x1+0x2..+0xn=b b не равно 0.(не имеет решений) Далее приводим систему к
ступенчатому виду и смотрим, не появилось ли это уравнение. И приводим систему
к ступенчатому виду. Если система принимает вид треугольника),сло лесенок
совпадает с числом неизвестных ) то система имеет одно единственное решение 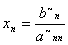
. Если система к треугольному виду не привелась т.е остаётся ступенчатый вид, то
она имеет бесконечное множество решений. Для однородной системы линейных
уравнений при решении методом гаусса если число уравнений меньше числа
неизвестных то система имеет не нулевое решение.
10 Рангом матрицы называется наивысший порядок Минора этой матрицы
отличного от нуля. Минор матрицы наивысший порядок которого совпадает с рангом
матрицы и отличный от 0 называется базисным минором матрицы. Чтобы найти ранг
матрицы можно воспользоваться методом гаусса и привести её к ступенчатому виду.
И ранг будет равен числу отличных от нуля элементов стоящих на ступеньке.
11 Свободными в системе уравнений называются элементы матрицы со
свободными членами, базисными называются
12 Векторы, лежащие на одной прямой или на параллельных прямых,
называются коллинеарными(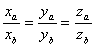
.) Векторы a b c называются компланарными, если они лежат в одной
плоскости или же находятся в параллельных плоскостях. (a*b)c=0 – компланарны
13 Сложение, умножение вектора на число называется линейными операциями
над векторами.
14 Сложение происходит по правилу треугольника (a+b называется вектор,
который идет из начала вектора а в конец вектора b при условии, что вектор b
приложен к концу вектора а), правило параллелограмма ( если векторы а и b
приведены к общему началу и на них построен параллелограмм то сумма равна
диагонали идущего из начала а и b. a+b=b+a коммутативность.
1) при сложении координаты складываются.2) При умножении на число умножитель
умножается на все координаты вектора.
15 Для любых трёх векторов (неколлинеарных)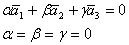 
Три неколлинеарные вектора 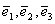
и неравные нулю называются базисом на плоскости. Любой вектор 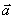
в пространстве может быть представлен в виде линейной комбинации базисных
векторов 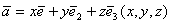
называется координатами данного вектора в данном базисе.(Совокупность n-линейно
независимых x векторов n мерного пространства называется базисом.
16. вектор an называется линейной комбинацией векторов если am=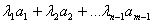
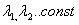 a1,a2... векторы. a1,a2... векторы.
Векторы a1,a2,an называются линейно зависимыми если найдётся отличные от нуля
числа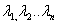 что выполняется что выполняется 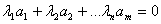
.
Если для векторов a1,a2,an равенство 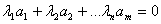
выполняется при условии 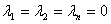
то такие вектора называются линейно независимыми. Если система векторов состоит
из одного вектора она будет являться линейно зависимой если вектор не равен 0
a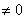 , а линейно , а линейно
зависимой если а=0 . Если среди векторов а1,а2,аn имеется нулевой вектор то
такая система линейно –зависима. 2) Если часть векторов системы а1,а2, линейно
зависима то все векторы линейно зависимы 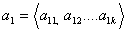 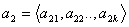
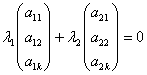 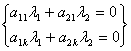
Если ранг матрицы данной системы равен количеству компонент то система
является линейно независимой.
17
Базис векторов называется ортонормированным если вектора ортогональны(угол
между ними 90)и имеют еденичные нормы(i j k)
18 Декартова прямоугольная система координат в пространстве определяется
заданием линейной единицы для измерения длин и тех пересекающихся в одной точке
взаимно перпендикулярных осей. Точка пересечения осей называется началом
координат, а сами оси – осями координат. Первая координатная ось называется
осью абсцисс, вторая – ординат. Третья – аппликат. Начало координат
обозначается буквой О оси: Ох, Оу, Оz.
19 Полярная система координат определяется заданием некоторой точки О,
называемой полюсом, луча ОА, исходящего из этой точки, называемой полярной
осью, и масштаба для измерения длин. Кроме того должны указывается какие
повороты вокруг точки О являются положительными какие отрицательными.
Координаты точки М задаются расстоянием ОМ и углом АОМ.
20
21 Скалярным произведение 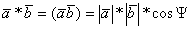
Свойства. 1)некоммутативность: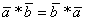
2)дистрибутивность 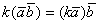
3)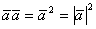 4) свойства знака 4) свойства знака 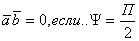
Если два вектора перпиндикулярны их скалярное произведение равно 0 и наооборот5)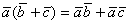
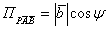 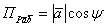 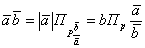
Произведение в координатных форме 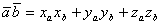 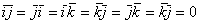
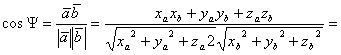
Страницы: 1, 2
| 


