| Шпора: Шпоргалки для первокурсников |
Шпора: Шпоргалки для первокурсников
1
Определение. Ф-я F(x) назыв. первообразной для ф-и f(x) на нек.
множестве Х, если в каждой точке этого рав-ва выполн. условие:
F'(x) = f(x)
Теорема1.
Если ф-я f(x) имеет 2 первообразные F1(x) и F2(x), то
разность м-у ними равна пост. числу, т.е.
F1(x) - F2(x) = C, где С- пост.
Доказательство: т.к. F1 и F2 по условию
первообразные, то имеет место два равенства:
F1'(x) = f(x)
F2'(x) = f(x)
Обозначим F1(x) - F2(x) = φ(x), продифференцируем
последнее равенство, используя два неравенства: F1'(x) - F2
'(x) = f(x) - f(x) = 0.
Т.о. φ'(x) = 0, видно, что функция φ(x) постоянна, воспользуемся
теоремой Лагранжа для φ(x), хÎ[a,b]: φ(x) - φ(a) =
φ'(ξ)(x - a) x<ξ<a
Т.к. φ(x) - φ(a) = 0 → φ(x) = φ(a) в любой точке
промежутка Х, то φ(а) = С - постоянная, получаем, что F1(x) - F
2(x) = C, теорема доказана.
Определение. Если ф-я f(x) имеет первообразную F(x), то выраж-е вида
F(x)+C назыв. неопред. интегралом от ф-и f(x)и обозн. ∫f(x)dx
Т.о. ∫f(x)dx = F(x) + C, если F'(x) = f '(x), здесь
f(x) - подинтегральная функция.
f(x)dx - подинтегральное выражение.
Операция нахождения первообразной для данной ф-и назыв. Интегрированием ф-и.
Теорема 2. (существования неопределенного иноеграла)
Если подинтерг. ф-я f(x) непрерывна на нек. множестве Х, то для неё
существует первообразная F(х), а след-но и неопред. интеграл
2
Непосредственно из опред. интеграла следует:
1.Если F(x) = f(x), то производная от неопред. интеграла равна подынтегр. ф-
и, т.е. (∫f(x)dx)' = (F(x) + C)' = f(x)
2.Дифференциал от неопред. интеграла равен подынтегральному выражению, т.е.
d (∫f(x)dx) = f(x)dx
d (∫f(x)dx) = (∫f(x)dx)' dx = f(x)dx
3.Интеграл от дифф. некоторой ф-и равен этой ф-и + произв. постоянная, т.е.
∫d F(x) = F(x) + C
f(x)dx = d F(x), откуда ∫d F(x) = F(x) + C
Док-во следует из почленного дифф. обоих частей по Х.
Замечание. Знаки дифференциала и интеграла, стоящие рядом, как бы
сокращают друг друга.
4.Постоянный множитель вынос. за знак неопр. интеграла, т.е.
∫α f(x)dx = α ∫f(x)dx
Можно док-ать, если продифф. Обе части по Х и исп-ть св-во
(∫αf(x)dx)' = α (∫f(x)dx)', получаем слева и справа
α*f(x) = α*f(x)
На осн. следует a f(x) = d f(x).
5.Неопр. интеграл от алгебр. суммы 2-х и более ф-ий равен такой же сумме
неопред. интегралов – слагаемых, т.е. ∫(f1(x) ± ∫f2
(x))dx = ∫f1(x)dx ± ∫f2(x)dx
Док-во аналогично предыдущей части.
3
Рассмотрим ∫f(x)dx. Пусть мы сразу не можем найти первообразную для ф-и
f(x). Заменим перем. х другой перм. t по формуле х=j(t), где j(t) – дифф. ф-
я на некот. промежутке Х, тогда очевидно: dx = j’(t)dt.
Таким. обр. ∫f(x)dx = ∫f[φ(t)]*φ'(t)dt
Доказательствово.
Найдем произв. от перем. t от левой и право частей рав-ва.
Имеем слева: Имеем справа:
(∫f(x)dx)' = (∫f(x)dx)'x* x't =
(∫f[φ(t)]* φ'(t)dx)' =
= f(x)* φ'(t) = f[φ(t)]* φ'(t) =
f[φ(t)]* φ'(t)
Т. обр. произв. слева и справа равны Þ на основании Т. Лагранжа левые и
правые части рав-ва одинаковы.
Доказанная ф-ла показ., что дост. вып-нить замены перем. в подынтегр. выр-
нии. Причем часто вместо замены x=j(t) провод. замена t=y(x), где y(х) -
дифф-я функция от х.
Удачная замена перм. часто позволяет упростить интеграл, а иногда свести его
к табличному.
Метод интегрирования по частям.
(u v)’ = u’ v + u v’ , где u = u(x); v = v(x).
d (u v) = (u’ v + u v’)dx = v u’dx + u v’dx =
d (u v) = v du + u dv.
Проинт. обе части этого рав-ва по х, получим
∫d (u v) = ∫v du + ∫u dv или ∫d(u*v) = u*v
∫u dv = u*v - ∫v du
Эта ф-ла применима, если подынт. выраж-е удается представить в виде проив-я
нек. ф-и и дифференциала dv другой ф-и v, причем обозначения u и dv должны
быть такими, чтобы вычисл. интегр. v du было бы более легкой задачей, чем
вычисление исх. интергала.
К интегрированию по частям приводят интегралы след. типа: ∫xne
xdx, ∫xn cosbx dx, ∫xn sinax dx,
∫xn lnx dx, ∫xn arcsinx dx, ∫xn
arccosx dx и др.
4
Простейшими рацион. дробями назыв. дроби след. вида:
I. А/(х-а), где А, а – числа
II. А/(х-а)к, где k – число >1.
III. (Ах+В)/(х2+рх+q), где (p2/u) - q = D
< 0. Квадратный трехчлен не имеет действительных корней. A, B, p, q - числа.
IV. (Ах+В)/(х2+рх+q)к, где k > 1 - целое число, (p2/u) - q = D < 0
Рассм. интегралы от этих дробей.
I. ∫ А/(х-а) dx = A ln│x-a│+ C
II. ∫ А/(х-а)к dx = A ((x - a)-k+1/(-k+1)) + C
III. ∫(Ах+В)dx/(х2+рх+q) = A/2 ∫(2x+p)dx/(х2
+рх+q) - Ap/2 - B ∫ dx/(х2+рх+q)
(х2+рх+q)' = 2x+p
Ax+B = (2x+p) A/2 - Ap/2 +B
Выделим сначала произ. знаменателя.
В первом из этих интегралов, как видно, числитель – произв. знам-ля Þ он
будет равен логарифму знам-ля, т.е. ∫(2x+p)dx/(х2+рх+q) =
ln│х2+рх+q│+ C
Во втором из этих интегралов выделяем полный квадрат и затем сводим к arctg,
получим ∫dx/(х2+рх+q) = 2/√4q - p2 * arctg
(2x+p)/√4q - p2 + C
Чтобы применять следующую формулу надо проверять дискриминант:
∫(Ах+В)dx/(х2+рх+q)=A/2 ln│х2
+рх+q│-(Ap-2B)/√4q - p2 * arctg (2x+p)/√4q - p
2 + C
IV. Для дроби этого типа существ. рекур. ф-лы., позволяющие
понижать k до единицы.
5
Рацион. дроби назыв. правильными, если показатель степени числ. дроби меньше,
показателя знаменателя.
Всякая неправильная раион. дробь может быть представлена в виде суммы
многочлена т прав. рацион. дроби.
Q(x)/P(x) = M(x) + Q1(x)/P1(x)
Далее для интегрирования прав. рацион. дроби её предс. в виде суммы дробей,
указ. выше типов, руководствуясь след. утверждением:
Если знам-ль правой рац. дроби предст. в виде разложения
Q(x)/P(x) = P(x)/((x-a)α * (x2+px+q)β) =
То имеет место след. утверждение:
= A1/(x-a) + A2/(x-a)2 + Aα
/(x-a)α + (M1x + N1)/(x2+px+q)
+ (M2x + N2)/(x2+px+q)2 + . + (M
βx + Nβ)/(x2+px+q)β
Как видно из посл. рав-ва правая часть предс. собой сумму простейших дробей,
при этом каждому действит. однокр. корню соответствует простейшая дробь 1
типа. Каждому кратному действ. корню соотв. простейшие дроби 1 и 2 типов.
Если корень знам-ля комплексное число (D<0), то такому корню соотв.
простейшая дробь.
Каждому комплекс. корню соотвт. простейшая дробь 4 типа.
6
Универсальная тригонометрическая подстановка
Рассм. интегралы вида ∫R(sinx, cosx)dx , где R - рациональная функция.
Интегралы такого вида берутся с помощью универсальной тригонометрической
подстановки: tg(x/2) = t
Выразим sin x, cos x с помощью tg половинного угла, имеем:
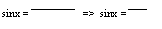 2tg(x/2) 2t
1+tg2(x/2) 1+t2 2tg(x/2) 2t
1+tg2(x/2) 1+t2
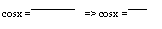 1- tg2(x/2) 1- t2
1+tg2(x/2) 1+t2
2dt
1+t2 1- tg2(x/2) 1- t2
1+tg2(x/2) 1+t2
2dt
1+t2
 2dt 1- t2 2dt
1+t2 1+t2 1+t2
Частные случаи подстановок.
Рассм. подстановки, кот. быстрее приводят к цели в нек. случаях, чем
предыдущая подстановка.
1. ∫R(sinx, cosx)dx, где R – нечетная ф-я относ-но sin х, тогда
делаем подстановку cos x = t и под знаком ∫ выполняем все действия,
заменяя х на t.
2. Если R- нечетная ф-я относ. cos x, то sin x = t.
3. ∫simmx * cosnx dx
а) из m, n – явл. нечетными, если n- нечетное, то примен. подстановка х=t.
Если m – нечетное, то примен. подстановка cos x = t.
б) оба показателей m, n – четные полож. числа. В этом случае степень
подынтгр. выраж-я пониж. С помощью тригон. ф-л:
sin2x = (1-cos2x)/2, cos2x = (1+cos2x)/2,
sinx * cosx = 1/2 sin2x
2dt 1- t2 2dt
1+t2 1+t2 1+t2
Частные случаи подстановок.
Рассм. подстановки, кот. быстрее приводят к цели в нек. случаях, чем
предыдущая подстановка.
1. ∫R(sinx, cosx)dx, где R – нечетная ф-я относ-но sin х, тогда
делаем подстановку cos x = t и под знаком ∫ выполняем все действия,
заменяя х на t.
2. Если R- нечетная ф-я относ. cos x, то sin x = t.
3. ∫simmx * cosnx dx
а) из m, n – явл. нечетными, если n- нечетное, то примен. подстановка х=t.
Если m – нечетное, то примен. подстановка cos x = t.
б) оба показателей m, n – четные полож. числа. В этом случае степень
подынтгр. выраж-я пониж. С помощью тригон. ф-л:
sin2x = (1-cos2x)/2, cos2x = (1+cos2x)/2,
sinx * cosx = 1/2 sin2x
Интегралы вида ∫tgmx dx, ∫ctgmx dx
Для нахождения этих интегралов примен. ф-лы, с пом. кот. помлед-но понижается
степень m.
tg2x = (1/cos2x) - 1, ctg2x = (1/sin2x) - 1
1/cosx = secx, 1/sinx = cosecx
tg2x = sec2x - 1, ctg2x = cosec2x - 1
Замечание.
Если m-степень частная, то удобно делать подст. tg x = t., тогда x = arctg t.
dx = dt/ (1+t2) и интеграл сводится к интегралу от непр. рацион. дроби.
Интегралы вида ∫ sin mx * cos nx dx, ∫ cos mx * cos nx dx,
∫ sin mx * sin nx dx/
В этом случае примен. след. тригон. функции:
sin mx * cos nx = ½ (sin (m+n) + sin (m-n))
cos mx * cos nx = ½ (cos (m+n) +cos (m-n))
sin mx * sin nx = ½ (cos (m-n) – cos (m+n))
Эти формулы дают нам произведение предс. в виде суммы.
Интегрирование нек. иррациональностей.
Интегралы вида ∫R (x, m√ax+b )
Такие интегралы наход. подстановкой ax+b = tm.
Интегралы вида ∫ ((Mx+N)dx)/((x-α) √ax2+bx+c )
x - α = 1/t
dx = -1/t2 dt
Тригонометрические подстановки.
∫R (x, √a2-x2 ) dx, ∫R (x, √a2+x2 ) dx
Чтобы избавиться от корня и привести интегралы к рацион. тригон. виду,
примен. подстановки.
Подстановка для первого: x = a sint (x = a cost)
Подстановка для второго: x = a tgt
Если под знаком Ö содерж. кв. трехчлен, то выделяем полный квадрат.
Существует ряд интегралов, не берущ. в элемент. ф-ях, т.е. для подынтг. ф-и
нельзя найти первообразную:
∫(sinx/x) dx - интегральный синус
∫(cosx/x) dx - интегральный косинус
∫е-x^2 dx - интеграл вероятности
∫(lnx/x) dx и др.
7
y = f(x) – непрерывна на отрезке [a;b].
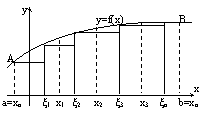 аАВв – криволинейная трапеция.
Вычислим площадь трапеции: Q - ?
Разобьем отр. [a;b] точками на частичный отрезки произ. образом. X0 =
а, х1,х2.xn = b.
Длину каждого их этих отрезков обозначим через Δxi=(i=1,2,.,n),
Δx1=x1-xo, Δx2=x2
-x1. Δxi=xi-xi-1
На каждом из частных отрезков построим прямоуг-ки с основаниями DXi с высотой
f(ξi)
ΔSi = Δxi * f(ξi), где i=1,2,.,n
- площадь каждого из прямоугольников.
Сумма всех площадей:
∑∆Si ≈ 0 = ∑ f(ξi) * ∆Si
Очевидно тем точнее, чем больше n (мелк. отрезков), т.е. сумма, стоящая
слева этого рав-ва назыв. интегральной суммой на отрезке [а;b].
Значение этой суммы зависит как от способа деления отрезка [a,b] на частичные,
так и от выбора точек x. Очевидно, точное значение искомой площади мы можем
получить, если в рав-ве перейти к пределу при n®¥ или (DXi®0).
Т. обр.
Q = lim ∑ f(ξi) * ∆xi
аАВв – криволинейная трапеция.
Вычислим площадь трапеции: Q - ?
Разобьем отр. [a;b] точками на частичный отрезки произ. образом. X0 =
а, х1,х2.xn = b.
Длину каждого их этих отрезков обозначим через Δxi=(i=1,2,.,n),
Δx1=x1-xo, Δx2=x2
-x1. Δxi=xi-xi-1
На каждом из частных отрезков построим прямоуг-ки с основаниями DXi с высотой
f(ξi)
ΔSi = Δxi * f(ξi), где i=1,2,.,n
- площадь каждого из прямоугольников.
Сумма всех площадей:
∑∆Si ≈ 0 = ∑ f(ξi) * ∆Si
Очевидно тем точнее, чем больше n (мелк. отрезков), т.е. сумма, стоящая
слева этого рав-ва назыв. интегральной суммой на отрезке [а;b].
Значение этой суммы зависит как от способа деления отрезка [a,b] на частичные,
так и от выбора точек x. Очевидно, точное значение искомой площади мы можем
получить, если в рав-ве перейти к пределу при n®¥ или (DXi®0).
Т. обр.
Q = lim ∑ f(ξi) * ∆xi
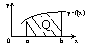 Определение. Если при любых делениях отрезка [а;b] таких, что DXi®0 и
при любом выборе точек xi на этих отрезках, интегральная сумма ® к
одному и тому же пределу, то этот предел назыв. опред. интегралом от ф-и y=
f(x) на отрезке [a;b] и обозначают ∫ f(x) dx
Определение. Если при любых делениях отрезка [а;b] таких, что DXi®0 и
при любом выборе точек xi на этих отрезках, интегральная сумма ® к
одному и тому же пределу, то этот предел назыв. опред. интегралом от ф-и y=
f(x) на отрезке [a;b] и обозначают ∫ f(x) dx
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



