|
|
| Диплом: Когомологии де Рама |
|
/td> |
+ |
|
 Продолжим
Продолжим 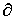 по
линейности до отображения по
линейности до отображения 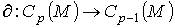 . Для бесконечных цепей отображение определяется аналогично:
. Для бесконечных цепей отображение определяется аналогично:
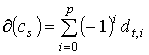 , , 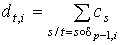 .
То есть для каждой р-цепи с (р-1)-цепь .
То есть для каждой р-цепи с (р-1)-цепь 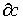 сопоставляет (р-1)-мерному сингулярному симплексу t число
сопоставляет (р-1)-мерному сингулярному симплексу t число 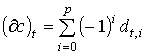 . Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение
. Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение 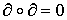 .
Из определения р-цепи следует, что равенство
.
Из определения р-цепи следует, что равенство 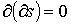 достаточно доказать для любого симплекса, тогда оно верно и для любой цепи.
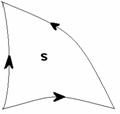
Пусть s есть q-мерный симплекс. Если
достаточно доказать для любого симплекса, тогда оно верно и для любой цепи.
Пусть s есть q-мерный симплекс. Если 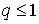 , то доказывать нечего. Если , то доказывать нечего. Если 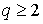 , то , то
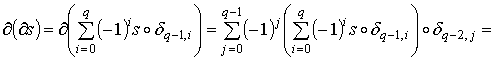
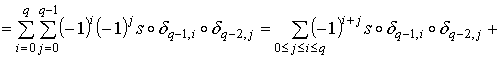
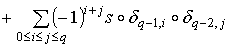 .
Так как .
Так как 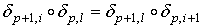 , то в нашем случае получим , то в нашем случае получим
 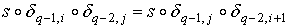 , если , если 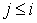 .
Тогда .
Тогда
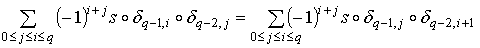
 положим
положим 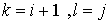
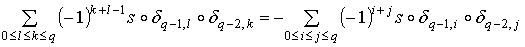 .
Таким образом, равенство
.
Таким образом, равенство 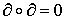 доказано. доказано.
1.3 Интегралы по р-мерным цепям.
Определение. р-цепь с, удовлетворяющая условию 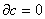 называется циклом; р-цепь вида
называется циклом; р-цепь вида 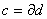 , где d – некоторая (р+1)-цепь называется границей.
Равенство
, где d – некоторая (р+1)-цепь называется границей.
Равенство 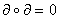 говорит о
том, что пространство границ есть подпространство пространства циклов.
Определение. Факторпространство пространства циклов по
пространству границ называется р-мерной группой гомологий и обозначается говорит о
том, что пространство границ есть подпространство пространства циклов.
Определение. Факторпространство пространства циклов по
пространству границ называется р-мерной группой гомологий и обозначается 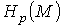 . Для бесконечных цепей р-мерная группа гомологий обозначается
. Для бесконечных цепей р-мерная группа гомологий обозначается 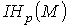 Из определения следует, что если
Из определения следует, что если 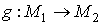 , то отображение
, то отображение 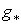 перестановочно с
перестановочно с 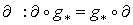 .
Поэтому .
Поэтому 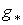 переводит
циклы в циклы, границы в границы.
Теперь рассмотрим дифференциальные формы и операцию внешнего дифференцирования
Определение. Носителем формы ω называется наименьшее
замкнутое множество, вне которого она равна нулю.
Определение. Дифференциальная р-форма ω называется
замкнутой, если переводит
циклы в циклы, границы в границы.
Теперь рассмотрим дифференциальные формы и операцию внешнего дифференцирования
Определение. Носителем формы ω называется наименьшее
замкнутое множество, вне которого она равна нулю.
Определение. Дифференциальная р-форма ω называется
замкнутой, если 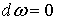 и
точной, если и
точной, если 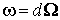 .
Замкнутые формы будем называть коциклами, точные – кограницами.
Из равенства .
Замкнутые формы будем называть коциклами, точные – кограницами.
Из равенства 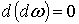 следует, что пространство кограниц есть подпространство пространства коциклов.
Определение. Факторпространство замкнутых р-форм по точным
р-формам называется р-мерной группой когомологий (де Рама) многообразия М и
обозначается
следует, что пространство кограниц есть подпространство пространства коциклов.
Определение. Факторпространство замкнутых р-форм по точным
р-формам называется р-мерной группой когомологий (де Рама) многообразия М и
обозначается 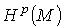 Определение. Факторпространство замкнутых р-форм с компактным
носителем по точным р-формам с компактным носителем называется р-мерной группой
когомологий с компактным носителем многообразия М и обозначается
Определение. Факторпространство замкнутых р-форм с компактным
носителем по точным р-формам с компактным носителем называется р-мерной группой
когомологий с компактным носителем многообразия М и обозначается 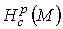 Заметим, что для компактного многообразия носитель формы всегда является
компактным множеством. Тогда группа когомологий совпадает с группой
когомологий с компактным носителем.
Определим интеграл от р-формы по р-цепи:
Определение. Пусть s – сингулярный р-симплекс, а
Заметим, что для компактного многообразия носитель формы всегда является
компактным множеством. Тогда группа когомологий совпадает с группой
когомологий с компактным носителем.
Определим интеграл от р-формы по р-цепи:
Определение. Пусть s – сингулярный р-симплекс, а 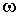 – дифференциальная форма степени р. Форма
– дифференциальная форма степени р. Форма 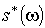 определена в некоторой окрестности евклидова р-симплекса
определена в некоторой окрестности евклидова р-симплекса 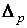 . Допустим, что,
. Допустим, что, 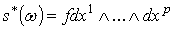 где
где 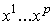 - стандартные
координаты в - стандартные
координаты в 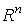 .
Положим по определению, .
Положим по определению, 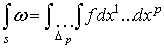 (1.3)
Продолжим (1.3) на любую конечную р-цепь по линейности. В общем случае нельзя
интегрировать произвольную р-форму по бесконечной р-цепи, так как это может
привести к расходящемуся бесконечному ряду.
Если ω – форма с компактным носителем, то для любой бесконечной цепи
(1.3)
Продолжим (1.3) на любую конечную р-цепь по линейности. В общем случае нельзя
интегрировать произвольную р-форму по бесконечной р-цепи, так как это может
привести к расходящемуся бесконечному ряду.
Если ω – форма с компактным носителем, то для любой бесконечной цепи 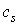 сумма
сумма  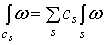 имеет только конечное число ненулевых членов и поэтому определена.
Пусть
имеет только конечное число ненулевых членов и поэтому определена.
Пусть 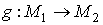 -
собственное дифференцируемое отображение. Из определения следует, что -
собственное дифференцируемое отображение. Из определения следует, что 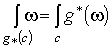 , так как
, так как 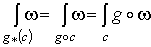 и и 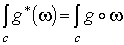 .
.
1.4 Теорема Стокса.
Теорема Стокса. Для любой р-цепи с и (р-1)-формы 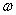 (соответственно бесконечной р-цепи с и (р-1)-формы с компактным носителем)
справедливо равенство
(соответственно бесконечной р-цепи с и (р-1)-формы с компактным носителем)
справедливо равенство 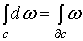 Доказательство.
Благодаря линейности по с обеих частей формулы
Доказательство.
Благодаря линейности по с обеих частей формулы 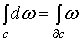 достаточно рассмотреть случай
достаточно рассмотреть случай 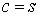 , где
, где 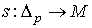 - сингулярный
р-симплекс. В этом случае наша формула сводится к равенству - сингулярный
р-симплекс. В этом случае наша формула сводится к равенству
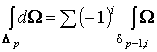 , (1.4)
где , (1.4)
где 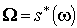 , а , а 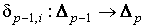 рассматривается как сингулярный (р-1)-симплекс в
рассматривается как сингулярный (р-1)-симплекс в 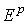 . По определению . По определению
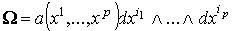 .
Достаточно доказать формулу (1.4) для каждого члена этой суммы. Таким
образом, задача сводится к проверке равенства .
Достаточно доказать формулу (1.4) для каждого члена этой суммы. Таким
образом, задача сводится к проверке равенства
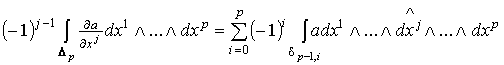 . (1.5)
Так как
. (1.5)
Так как 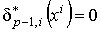 , то в
правой части останутся только члены с , то в
правой части останутся только члены с 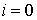 и
и 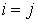 . Пусть . Пусть 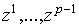 – евклидовы координаты в
– евклидовы координаты в 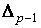 . Тогда
. Тогда
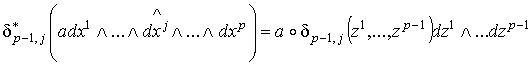 и
и 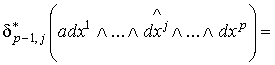
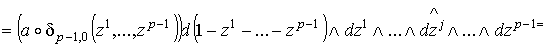
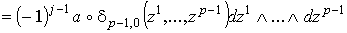 .
В соответствии с определениями (1.5) сводится к равенству .
В соответствии с определениями (1.5) сводится к равенству
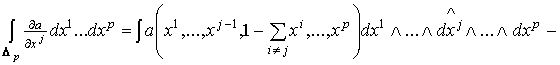
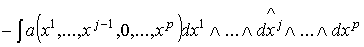 .
Из равенства .
Из равенства 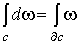 следует, что интегралы точной формы по циклу и замкнутой формы по границе равны
нулю. Таким образом, справедливы следующие следствия:
Следствие 1. Билинейное отображение
следует, что интегралы точной формы по циклу и замкнутой формы по границе равны
нулю. Таким образом, справедливы следующие следствия:
Следствие 1. Билинейное отображение 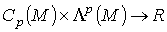 ,определяемое интегралом
,определяемое интегралом 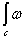 , индуцирует билинейное отображение
, индуцирует билинейное отображение 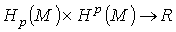 .
То есть отображение
.
То есть отображение 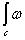 является билинейным и не зависит от выбора представителя.
Рассмотрим замкнутую р-форму ω и р-цикл с, такие что является билинейным и не зависит от выбора представителя.
Рассмотрим замкнутую р-форму ω и р-цикл с, такие что 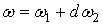 и и 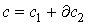 . Тогда . Тогда
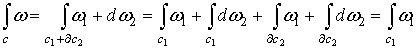 .
Аналогично следствию 1 получаем:
Следствие 2. Билинейное отображение
.
Аналогично следствию 1 получаем:
Следствие 2. Билинейное отображение 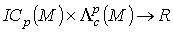 ,определяемое интегралом
,определяемое интегралом 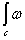 , индуцирует билинейное отображение
, индуцирует билинейное отображение 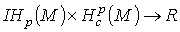 .
.
Раздел 2. Нульмерные и n-мерные когомологии.
Согласно определению, не существует нульмерных кограниц. Поэтому нульмерная
группа когомологий совпадает с группой коциклов. Но 0-форма есть просто
функция, а 0-коцикл есть такая функция f, что 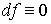 , то есть локально постоянная функция. Таким образом,
, то есть локально постоянная функция. Таким образом, 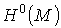 является пространством всех локально постоянных вещественных функций на М
. Поскольку любая локально постоянная функция постоянна на связных компонентах
многообразия М, то
является пространством всех локально постоянных вещественных функций на М
. Поскольку любая локально постоянная функция постоянна на связных компонентах
многообразия М, то 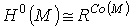 , где Со(М) есть множество компонент в М. В частности, если
М связно, то
, где Со(М) есть множество компонент в М. В частности, если
М связно, то 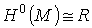 .
Функция f является компактным коциклом, если она локально постоянна и
supp f компактен. Это означает, что .
Функция f является компактным коциклом, если она локально постоянна и
supp f компактен. Это означает, что 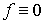 на некомпактных компонентах многообразия М. Поэтому
на некомпактных компонентах многообразия М. Поэтому 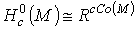 , где
, где 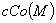 есть
множество компактных компонент многообразия М. В частности, если М
связно, то есть
множество компактных компонент многообразия М. В частности, если М
связно, то 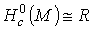 для
компактного многообразия М и для
компактного многообразия М и 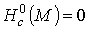 для некомпактного М.
для некомпактного М.
2.1 Вычисление когомологий на компактном многообразии.
Рассмотрим в 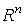 шар шар 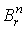 радиуса r. Тогда можно вычислить
радиуса r. Тогда можно вычислить 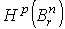 для всех р. Именно, справедлива
Теорема 2.1 (лемма Пуанкаре). Пусть w - форма степени
для всех р. Именно, справедлива
Теорема 2.1 (лемма Пуанкаре). Пусть w - форма степени 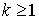 , определенная на
, определенная на 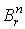 ,
и пусть ,
и пусть 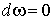 . Тогда
существует такая форма W, определенная на . Тогда
существует такая форма W, определенная на 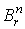 , что
, что 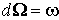 .
Докажем теорему индукцией по размерности n. Для .
Докажем теорему индукцией по размерности n. Для 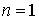 можно считать
можно считать 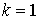 ; все
другие случаи тривиальны. Если ; все
другие случаи тривиальны. Если 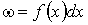 , то достаточно положить
, то достаточно положить 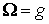 , где
, где 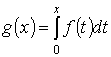 .
Сделаем следующее замечание:
Лемма 2.1. Если .
Сделаем следующее замечание:
Лемма 2.1. Если 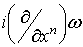 =0 и =0 и 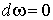 , то , то 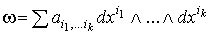 , где , где 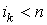 и и 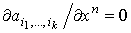 .
Действительно, .
Действительно,
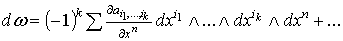 ,
где остальные члены не содержат ,
где остальные члены не содержат 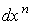 .
Перейдем к доказательству теоремы.
Пусть .
Перейдем к доказательству теоремы.
Пусть 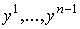 – декартовы координаты в – декартовы координаты в 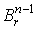 , и пусть , и пусть 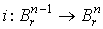 - отображение, задаваемое формулами - отображение, задаваемое формулами
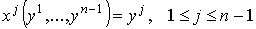 , ,
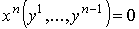 ,
где ,
где 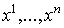 - декартовы
координаты в - декартовы
координаты в 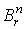 .
Тогда .
Тогда 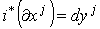 для для 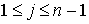 и
и 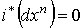 . Пусть р
– отображение шара . Пусть р
– отображение шара 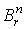 на
на 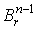 , определяемое
формулой , определяемое
формулой
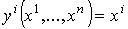 для для 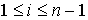 .
Имеем .
Имеем 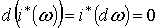 . По
предположению индукции . По
предположению индукции 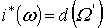 для некоторой формы
для некоторой формы 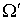 на
на 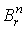 . Положим . Положим 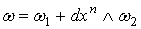 . Где
. Где 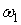 и и 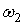 - формы от
- формы от  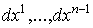 . Определим форму W следующими условиями:
1.
. Определим форму W следующими условиями:
1. 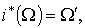 2.
2. 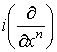 W=0,
3. W=0,
3. 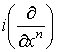 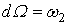 В терминах координат
В терминах координат 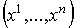 условие 2. означает, что форма W может быть записана в виде
условие 2. означает, что форма W может быть записана в виде
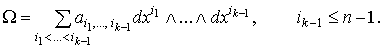 Условие 1. означает, что
Условие 1. означает, что 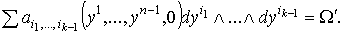 Условие 2. означает, что
Условие 2. означает, что 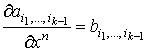 , если , если 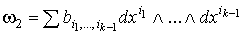 .
Отсюда видно, что существует единственная форма W, удовлетворяющая условиям
1,2,3, которая может быть найдена с помощью интегрирования по .
Отсюда видно, что существует единственная форма W, удовлетворяющая условиям
1,2,3, которая может быть найдена с помощью интегрирования по 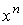 . Мы утверждаем, что
. Мы утверждаем, что 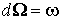 . Действительно,
. Действительно,
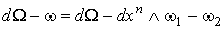 .
Но .
Но 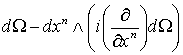 есть дифференциальная форма, не содержащая есть дифференциальная форма, не содержащая 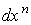 . Поэтому . Поэтому
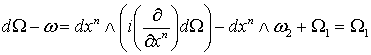 ,
где ,
где 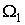 не зависит от не зависит от 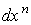 . Поскольку . Поскольку 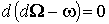 , мы можем применить лемму 2.1. Таким образом, , мы можем применить лемму 2.1. Таким образом,
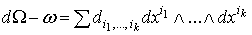 , где , где 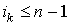 и и 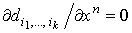 .
С другой стороны, .
С другой стороны,
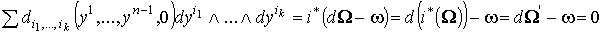 . Значит,
. Значит, 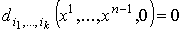 и и 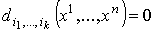 . Другими словами, . Другими словами, 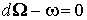 , что и доказывает теорему 2.1.
Следствие 2.1. , что и доказывает теорему 2.1.
Следствие 2.1. 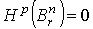 для для 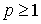 .
В доказательстве теоремы 2.1. коэффициенты формы W из коэффициентов формы w
интегрированием. Поэтому, если коэффициенты формы w дифференцируемо зависят
от некоторых дополнительных параметров, то форма W также дифференцируемо
зависит от этих параметров.
Следствие 2.2. Если в теореме 2.1. форма w дифференцируемо зависит от
параметров, то есть .
В доказательстве теоремы 2.1. коэффициенты формы W из коэффициентов формы w
интегрированием. Поэтому, если коэффициенты формы w дифференцируемо зависят
от некоторых дополнительных параметров, то форма W также дифференцируемо
зависит от этих параметров.
Следствие 2.2. Если в теореме 2.1. форма w дифференцируемо зависит от
параметров, то есть 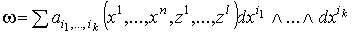 , где
, где 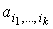 –
дифференцируемые функции от –
дифференцируемые функции от 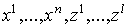 и
и 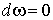 (оператор d
берется по (оператор d
берется по 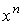 ), то ), то 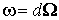 , где
, где 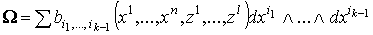 , причем , причем 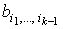 - дифференцируемые функции всех n+l переменных.
- дифференцируемые функции всех n+l переменных.
2.2 Вычисление когомологий с компактным носителем.
Мы хотим вычислить 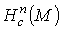 для любого многообразия М.
Лемма 2.2. Пусть w - такая n-форма, определенная на для любого многообразия М.
Лемма 2.2. Пусть w - такая n-форма, определенная на 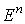 , что
1. supp , что
1. supp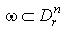 , где , где 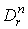 - куб - куб 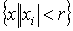 2.
2. 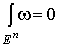 .
Тогда мы можем найти такую (n-1)-форму W, что
3. supp .
Тогда мы можем найти такую (n-1)-форму W, что
3. supp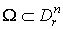 ,
4. ,
4. 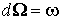 .
Доказательство:
Доказательство проведем с помощью индукции. Для любой k-формы p,
выраженной через .
Доказательство:
Доказательство проведем с помощью индукции. Для любой k-формы p,
выраженной через 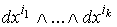 ,
обозначим символом ,
обозначим символом 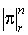 максимум абсолютных значений ее коэффициентов в
максимум абсолютных значений ее коэффициентов в 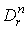 . Мы будем говорить, что семейство форм
. Мы будем говорить, что семейство форм 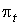 дифференцируемо зависит от t, если каждый коэффициент есть
дифференцируемая функция от
дифференцируемо зависит от t, если каждый коэффициент есть
дифференцируемая функция от 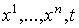 . Здесь t обозначает s-мерный параметр,
. Здесь t обозначает s-мерный параметр, 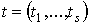 . Наше индуктивное предположение состоит в следующем:
Пусть
. Наше индуктивное предположение состоит в следующем:
Пусть 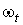 -
семейство форм на -
семейство форм на 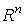 ,
дифференцируемо зависящее от t. Предположим, что для каждого значения t форма ,
дифференцируемо зависящее от t. Предположим, что для каждого значения t форма 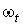 удовлетворяет условиям 1. и 2. Тогда существует такое дифференцируемое семейство
форм
удовлетворяет условиям 1. и 2. Тогда существует такое дифференцируемое семейство
форм 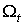 ,
удовлетворяющее условию 3., что ,
удовлетворяющее условию 3., что 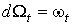 и
5.
и
5. 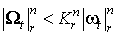 ,
где ,
где 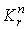 зависит только от n и r
Для зависит только от n и r
Для 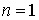 мы можем
написать мы можем
написать 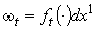 .
Определим функцию .
Определим функцию 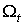 равенством
равенством 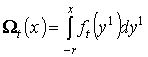 .Очевидно, что
.Очевидно, что 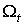 есть
дифференцируемое семейство 0-форм, удовлетворяющих условиям 3., 4. и 5.
Допустим, что предположение индукции выполнено для n-1. Пусть есть
дифференцируемое семейство 0-форм, удовлетворяющих условиям 3., 4. и 5.
Допустим, что предположение индукции выполнено для n-1. Пусть
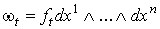 .
И пусть .
И пусть 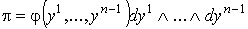 есть
положительная форма на есть
положительная форма на 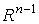 , такая, что supp
, такая, что supp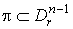 и
и 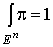 . Рассмотрим формы . Рассмотрим формы 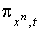 на
на 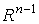 (зависящие от
параметров (зависящие от
параметров 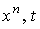 ),
определяемые формулой ),
определяемые формулой
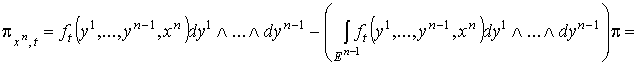
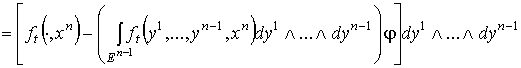 . (2.1)
Они образуют дифференцируемое семейство
. (2.1)
Они образуют дифференцируемое семейство 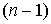 -форм, удовлетворяющее предположению индукции. Кроме того,
-форм, удовлетворяющее предположению индукции. Кроме того, 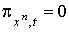 , если
, если 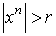 . Поэтому мы
можем написать . Поэтому мы
можем написать
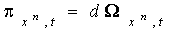 (2.2)
Пусть (2.2)
Пусть 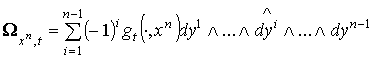 , где , где 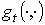 – дифференцируемые функции на – дифференцируемые функции на 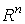 . Определим форму . Определим форму 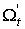 равенством равенством
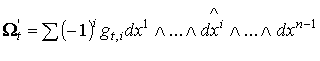 ,
так что ,
так что 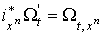 , где , где 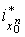 есть вложение есть вложение 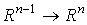 , заданное формулами , заданное формулами
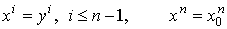 .
При вычислении формы .
При вычислении формы 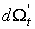 встретятся два типа членов: содержащие частные производные по
встретятся два типа членов: содержащие частные производные по 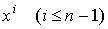 содержащие частную производную по
содержащие частную производную по 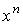 . Умножением на
. Умножением на 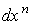 мы
избавимся от членов, содержащих мы
избавимся от членов, содержащих 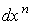 , и, значит для каждого значения
, и, значит для каждого значения 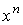 будем иметь
будем иметь 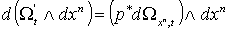 , где
р есть проекция , где
р есть проекция 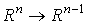 вдоль
вдоль 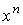 . Положим . Положим 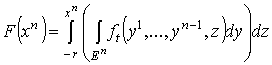 . Тогда
. Тогда 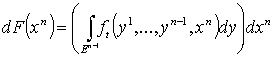 . Положим . Положим
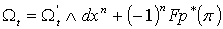 . (2.3)
Имеем . (2.3)
Имеем 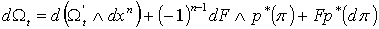 . Но . Но 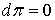 , поскольку p есть (n-1)-форма на , поскольку p есть (n-1)-форма на 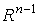 . Поэтому . Поэтому
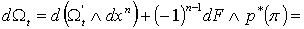
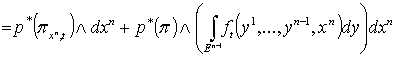 . (2.4)
Далее, формы . (2.4)
Далее, формы  p и p и 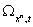 , а значит, и форма
, а значит, и форма 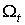 обращаются в нуль при
обращаются в нуль при 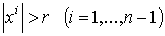 . Если
. Если 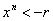 или или 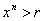 , то последний интеграл также обращается в нуль, поскольку
, то последний интеграл также обращается в нуль, поскольку
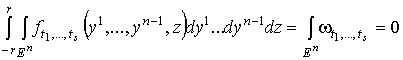 .
Форма
.
Форма 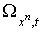 обращается в нуль, если обращается в нуль, если 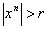 , так как по индуктивному предположению 5. , так как по индуктивному предположению 5.
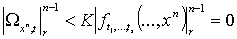 при при 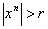 .
Наконец, формы встречающиеся в правой части формулы (2.3), очевидно образуют
дифференцируемое семейство форм и удовлетворяют оценке 5., где .
Наконец, формы встречающиеся в правой части формулы (2.3), очевидно образуют
дифференцируемое семейство форм и удовлетворяют оценке 5., где 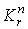 зависят от
зависят от 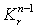 и
от выбора j. Лемма доказана.
С помощью леммы 2.2. доказывается
Лемма 2.3. Если М – связное n-мерное многообразие, то и
от выбора j. Лемма доказана.
С помощью леммы 2.2. доказывается
Лемма 2.3. Если М – связное n-мерное многообразие, то 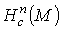 есть либо R, либо {0} (то есть
есть либо R, либо {0} (то есть 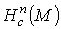 не более чем одномерно).
Пусть
не более чем одномерно).
Пусть 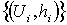 - такой атлас
на М, что каждая окрестность - такой атлас
на М, что каждая окрестность 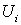 имеет вид
имеет вид 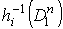 . Пусть W
- такая n-форма, что supp . Пусть W
- такая n-форма, что supp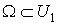 и
и 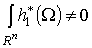 . Лемма будет
доказана, если для любой n-формы w с компактным носителем мы найдем
такое вещественное число с, что . Лемма будет
доказана, если для любой n-формы w с компактным носителем мы найдем
такое вещественное число с, что
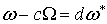 , (2.5)
где , (2.5)
где 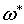 есть (n-1)
-форма с компактным носителем. Пусть есть (n-1)
-форма с компактным носителем. Пусть 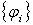 - разбиение единицы, подчиненное покрытию
- разбиение единицы, подчиненное покрытию 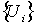 . Тогда
. Тогда 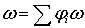 - конечная
сумма, и достаточно провести доказательство для каждого слагаемого в
отдельности. Поэтому можно считать, что supp - конечная
сумма, и достаточно провести доказательство для каждого слагаемого в
отдельности. Поэтому можно считать, что supp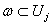 для некоторого j. Пусть р – точка из
для некоторого j. Пусть р – точка из 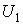 , а q – из
, а q – из 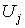 .
Пусть .
Пусть 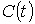 – такая
кривая, что – такая
кривая, что 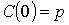 и и 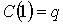 . Покроем
. Покроем 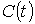 конечным
числом окрестностей конечным
числом окрестностей 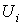 . Изменив, если потребуется, их нумерацию, мы можем считать, что это окрестности
. Изменив, если потребуется, их нумерацию, мы можем считать, что это окрестности 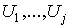 , причем
, причем 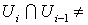 Æ
Пусть Æ
Пусть 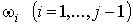 – такие
формы, что
supp – такие
формы, что
supp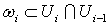 , , 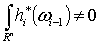 .
Положим .
Положим 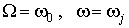 .
Рассмотрим формы .
Рассмотрим формы 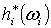 и и 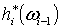 на
на 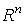 с носителями в с носителями в 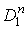 . Поскольку
. Поскольку 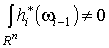 ,
существуют константы ,
существуют константы
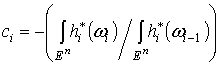 такие, что
такие, что 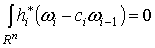 . По лемме 2.2. . По лемме 2.2.
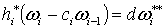 , (2.6)
причем supp , (2.6)
причем supp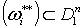 .
Форма .
Форма 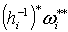 определена в определена в 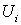 и имеет носитель в
и имеет носитель в 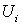 .
Определим на М форму .
Определим на М форму 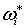 , полагая
, полагая 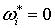 вне вне 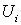 и
и 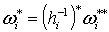 на на 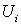 . Тогда равенство (2.6) можно переписать в виде
. Тогда равенство (2.6) можно переписать в виде
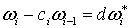 . (2.7)
Складывая с подходящими весами равенства (2.7) при . (2.7)
Складывая с подходящими весами равенства (2.7) при 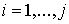 , мы получим равенство (2.5) , где
, мы получим равенство (2.5) , где
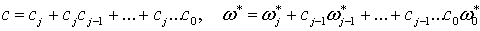 .
.
Литература.
1. Александров П.С. "Введение в теорию множеств и общую
топологию", Москва
2. Александров П.С., Пасынков Б.С. "Введение в теорию
размерности", Москва
3. Бураго Ю.Д., Залгаллер В.А. "Риманова геометрия", Санкт-
Петербург, Наука, 1994
4. Дубровин Б.А., Новиков С.П., Фоменко А.Т. "Современная
геометрия", Москва
5. Келли Дж. "Общая топология", Москва
6. Колмогоров А.Н., Фомин В.С "Элементы теории функций и
функционального анализа", Москва
7. Погорелов А.В. "Дифференциальная геометрия", Москва, Наука, 1969
8. Понтрягин Л.С. "Гладкие многообразия и их применение в теории
гомотопий", Москва, Наука, 1984
9. Постников М.М. "Группы Ли", Москва
10. Стернберг
11. Фоменко А.Т., Фукс Д.Б. "Курс гомотопической топологии", Москва,
Наука, 1989
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|




 Продолжим
Продолжим 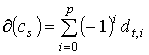 ,
, 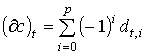 . Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение
. Тогда и в случае конечных и в случае бесконечных цепей имеет место соотношение 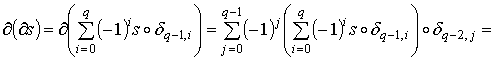
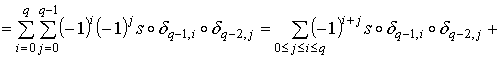
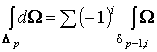 , (1.4)
где
, (1.4)
где 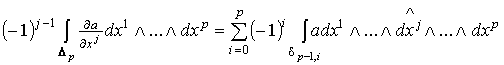 . (1.5)
Так как
. (1.5)
Так как 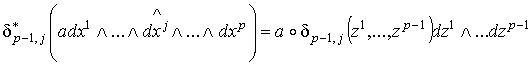 и
и 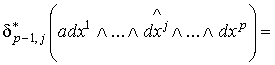
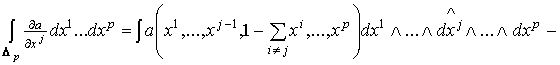
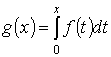 .
Сделаем следующее замечание:
Лемма 2.1. Если
.
Сделаем следующее замечание:
Лемма 2.1. Если 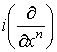 W=0,
3.
W=0,
3. 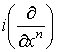
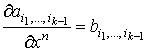 , если
, если 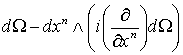 есть дифференциальная форма, не содержащая
есть дифференциальная форма, не содержащая 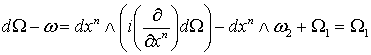 ,
где
,
где 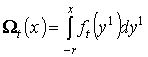 .Очевидно, что
.Очевидно, что 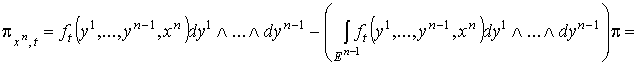
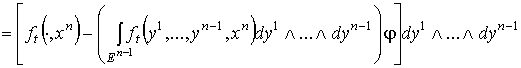 . (2.1)
Они образуют дифференцируемое семейство
. (2.1)
Они образуют дифференцируемое семейство 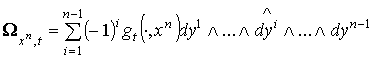 , где
, где 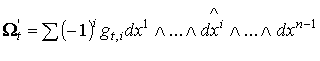 ,
так что
,
так что 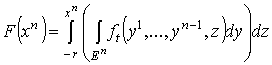 . Тогда
. Тогда 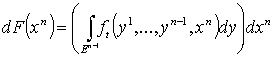 . Положим
. Положим
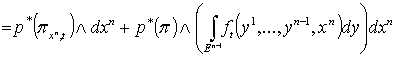 . (2.4)
Далее, формы
. (2.4)
Далее, формы 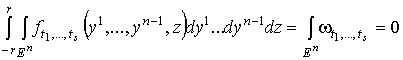 .
Форма
.
Форма  такие, что
такие, что