|
|
| Курсовая: Быстрые вычисления с целыми числами и полиномами |
Cmul(n) = =
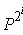  Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися
возведениями в квадрат), вычисления несколько сложнее: зная , вычисляем
с мультипликативной сложностью. Как следствие имеем:
Csqr(2l) =
=
=
=
Предварительное заключение, которое можно вывести из предыдущих вычислений,
складывается в пользу дихотомического возведения в степень: если n есть
степень двойки (гипотеза ad hoc), этот алгоритм ещё выдерживает конкуренцию,
даже если эта победа гораздо скромнее в данном контексте (n2
d2/3 против n2d2/2), чем
когда работаем в Z/pZ (2log2 n против n).
Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися
возведениями в квадрат), вычисления несколько сложнее: зная , вычисляем
с мультипликативной сложностью. Как следствие имеем:
Csqr(2l) =
=
=
=
Предварительное заключение, которое можно вывести из предыдущих вычислений,
складывается в пользу дихотомического возведения в степень: если n есть
степень двойки (гипотеза ad hoc), этот алгоритм ещё выдерживает конкуренцию,
даже если эта победа гораздо скромнее в данном контексте (n2
d2/3 против n2d2/2), чем
когда работаем в Z/pZ (2log2 n против n).
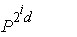 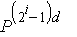 Но мы не учли корректирующие перемножения, которые должны быть выполнены, когда
показатель не является степенью двойки. Если n = 2l+1 – 1, нужно
добавить к последовательным возведениям в квадрат перемножения всех полученных
многочленов. Умножение многочлена степени (2i-1)
d на многочлен степени 2id вносит свой вклад
из ((2i – 1)d + 1)( 2i d + 1)
умножений, которые, будучи собранными по всем корректирующим вычислениям, дают
дополнительную сложность:
= =
Но мы не учли корректирующие перемножения, которые должны быть выполнены, когда
показатель не является степенью двойки. Если n = 2l+1 – 1, нужно
добавить к последовательным возведениям в квадрат перемножения всех полученных
многочленов. Умножение многочлена степени (2i-1)
d на многочлен степени 2id вносит свой вклад
из ((2i – 1)d + 1)( 2i d + 1)
умножений, которые, будучи собранными по всем корректирующим вычислениям, дают
дополнительную сложность:
= =
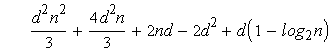 =
=
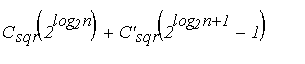 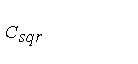 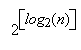 Теперь можно заключить, что дихотомическое возведение в степень не всегда
является лучшим способом для вычисления степени многочлена с помощью
перемножений многочленов. Число перемножений базисного кольца, которые
необходимы, Csqr(n), - в действительности заключено
между ( ) и
т.е. между n
2d2/3 и 2n2d2/3,
тогда как простой алгоритм требует всегда n2d2
/2 перемножений. В частности, если исходный многочлен имеет степень, большую или
равную 4, возведение в степень наивным методом требует меньше перемножений в
базисном кольце, чем бинарное возведение в степень, когда n имеет форму
2l – 1.
Можно довольно просто доказать, что если n имеет вид 2l
+2l – 1 + c (выражения,
представляющие двоичное разложение n), то метод вычисления
последовательными перемножениями лучше метода, использующего возведение в
квадрат (этот последний метод требует корректирующего счёта ценой, по крайней
мере, n2d2/9). Всё это доказывает, что
наивный способ является лучшим для этого класса алгоритмов, по крайней мере, в
половине случаев.
Действительно, МакКарти [3] доказал, что дихотомический алгоритм возведения в
степень оптимален среди алгоритмов, оперирующих повторными умножениями, если
действуют с плотными многочленами (антоним к разреженным) по модулю m,
или с целыми и при условии оптимизации возведения в квадрат для сокращения его
сложности наполовину (в этом случае сложность действительно падает
приблизительно до n2d2/6 + n2
d2/3 = n2d2/2).
3.3 Небольшие оптимизации для произведений многочленов
В принципе вычисление произведения двух многочленов степеней n и m
соответственно требует (n +1)( m +1) элементарных перемножений.
Алгоритм оптимизации возведения в квадрат состоит просто в применении формулы
квадрата суммы:
что даёт n +1 умножений для первого члена и n( n +1)/2 –
для второго, или в целом (n +1)( n +2)/2 умножений, что близко к
половине предусмотренных умножений, когда n большое.
Для произведения двух многочленов первой степени P = aX + b и
Q = cX + d достаточно легко находим формулы U = ac,
W = bd, V = (a + b)(c + d) и
PQ = =UX2 + (V – U – W)X +
W, в которых появляются только три элементарных умножения, но четыре
сложения. Можно рекурсивно применить этот процесс для умножения двух
многочленов P и Q степени 2l – 1, представляя
их в виде и применяя
предыдущие формулы для вычисления PQ в зависимости от A, B
, C и D, где каждое произведение AB, CD и (A
+ B)(C + D) вычисляется с помощью рекурсивного применения
данного метода (это метод Карацубы). Всё это даёт мультипликативную сложность
M(2l) и аддитивную сложность A(2l
) такие, что:
Теперь можно заключить, что дихотомическое возведение в степень не всегда
является лучшим способом для вычисления степени многочлена с помощью
перемножений многочленов. Число перемножений базисного кольца, которые
необходимы, Csqr(n), - в действительности заключено
между ( ) и
т.е. между n
2d2/3 и 2n2d2/3,
тогда как простой алгоритм требует всегда n2d2
/2 перемножений. В частности, если исходный многочлен имеет степень, большую или
равную 4, возведение в степень наивным методом требует меньше перемножений в
базисном кольце, чем бинарное возведение в степень, когда n имеет форму
2l – 1.
Можно довольно просто доказать, что если n имеет вид 2l
+2l – 1 + c (выражения,
представляющие двоичное разложение n), то метод вычисления
последовательными перемножениями лучше метода, использующего возведение в
квадрат (этот последний метод требует корректирующего счёта ценой, по крайней
мере, n2d2/9). Всё это доказывает, что
наивный способ является лучшим для этого класса алгоритмов, по крайней мере, в
половине случаев.
Действительно, МакКарти [3] доказал, что дихотомический алгоритм возведения в
степень оптимален среди алгоритмов, оперирующих повторными умножениями, если
действуют с плотными многочленами (антоним к разреженным) по модулю m,
или с целыми и при условии оптимизации возведения в квадрат для сокращения его
сложности наполовину (в этом случае сложность действительно падает
приблизительно до n2d2/6 + n2
d2/3 = n2d2/2).
3.3 Небольшие оптимизации для произведений многочленов
В принципе вычисление произведения двух многочленов степеней n и m
соответственно требует (n +1)( m +1) элементарных перемножений.
Алгоритм оптимизации возведения в квадрат состоит просто в применении формулы
квадрата суммы:
что даёт n +1 умножений для первого члена и n( n +1)/2 –
для второго, или в целом (n +1)( n +2)/2 умножений, что близко к
половине предусмотренных умножений, когда n большое.
Для произведения двух многочленов первой степени P = aX + b и
Q = cX + d достаточно легко находим формулы U = ac,
W = bd, V = (a + b)(c + d) и
PQ = =UX2 + (V – U – W)X +
W, в которых появляются только три элементарных умножения, но четыре
сложения. Можно рекурсивно применить этот процесс для умножения двух
многочленов P и Q степени 2l – 1, представляя
их в виде и применяя
предыдущие формулы для вычисления PQ в зависимости от A, B
, C и D, где каждое произведение AB, CD и (A
+ B)(C + D) вычисляется с помощью рекурсивного применения
данного метода (это метод Карацубы). Всё это даёт мультипликативную сложность
M(2l) и аддитивную сложность A(2l
) такие, что:
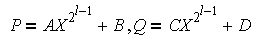 M(2l) = 3M(2l – 1),., M(2) = 3M(1), M(1) = 1,
A(2l) = 3A(2l – 1) + 3*2l,., A(2) = 3A(1) + 6, A(1) = 1.
В этой последней формуле член 3*2l представляет собой число
элементарных сложений, необходимых, чтобы сделать два сложения многочленов
степени 2l – 1 – 1 (a + b и c +
d) и два вычитания многочленов степени 2l – 1 (U –
V – W). Суммируя каждое из этих выражений, находим для n,
являющегося степенью двойки:
M(n) = nlog3/log2 » n1,585 и A(2) =7 nlog3/log2 – 6n.
К сожалению, этот принцип остаётся теоретическим, и на его основе нужно
построить итерационный алгоритм, чтобы получить разумную эффективность (цена
управления рекурсией очень велика).
3.4 Вычисление многочленов
Рассмотрим общую задачу вычисления многочлена n-й степени
u(x) = unxn + un –
1xn – 1 + ... + u1x
+ u0, un ¹ 0,
(1)
3.4.1 Схема Горнера
u(x) = (.(unx + un – 1)x + .)x + u0. (2)
Весь этот процесс требует n умножений и n сложений.
Было предложено несколько обобщений схемы Горнера. Посмотрим сначала, как
вычисляется в случае, когда – комплексное число, а коэффициенты вещественны.
Комплексное сложение и умножение можно очевидным образом свести к
последовательности обычных операций над вещественными числами:
вещественное + комплексное требует 1 сложение,
комплексное + комплексное требует 2 сложения,
вещественное * комплексное требует 2 умножения,
комплексное * комплексное требует 4 умножения и 2 сложения
или 3 умножения и 5 сложений.
Следовательно, схема Горнера (2) требует 4n – 2 умножений и 3n – 2
сложений или 3n – 1 умножений и 6n – 5 сложений для вычисления
u(z), когда z комплексное. Вот другая процедура для
вычисления u(x + iy):
a1 = un, b1 = un – 1, r = x + x, s = x2 + y2; (3)
aj = bj – 1 + raj –1, bj = un – j – saj –1, 1 < j £ n.
Легко доказать индукцией по n, что u(z) = zan
+ bn. Эта схема требует 2n + 2 умножений и 2n +
1 сложений, так что при n ³ 3 она лучше схемы Горнера.
Рассмотрим процесс деления многочлена u(x) на многочлен x – x
0. В результате такого деления мы получаем u(x) = (x
– x0)q(x) + r(x); здесь deg(r
) < 1, поэтому r(x) есть постоянная, не зависящая от x
и u(x0) = 0*q(x0) + r
= r. Анализ этого процесса деления показывает, что вычисления почти те
же самые, что в схеме Горнера для определения u(x0).
Аналогично, когда мы делим u(z) на многочлен (z – z
0)(z – z0) = z2 – 2x
0z + x02 + y0
2, то соответствующие вычисления эквивалентны процедуре (3); мы получаем
u(z) = (z – z0)(z – z0)q(z) + anz + bn;
следовательно,
u(z0) = anz0 + bn.
Вообще, когда мы делим u(x) на, f(x) получая u
(x) = f(x) q(x) + r(x), то
из равенства f(x0) = 0 следует u(x
0) = r(x0); это наблюдение ведёт к дальнейшим
обобщениям правила Горнера. Мы можем положить, например, f(x) =
x2 – x02; это даст нам схему
Горнера «второго порядка»
u(x) = (.(u2ë n/2 û x2 + u2ë n/2 û – 2)x2 + u0 +
+((..u2é n/2
ù - 1 x2 + u2
é n/2 ù - 3
)x2 + . +)x2u1) x.
(4)
3.4.2 Интерполяционная формула Ньютона и табулирование значений многочлена
Рассмотрим специальный случай вычисления многочлена. Интерполяционный многочлен
Ньютона степени n, определяемый формулой
u[n](x) = an(x – x
0) (x – x1).(x – xn
– 1) +.+ an (x – x0) (x
– x1) + a1 (x – x0) + a
0, (5)
является единственным многочленом степени £ n от x,
который принимает предписанные значения y0, y1
, ., yn в заданных n + 1 различных точках x
0, x1, ., xn соответственно. После
того, как значения постоянных a найдены, интерполяционная формула Ньютона
становится удобной для вычислений, так как мы можем, обобщив правило Горнера,
записать
u[n](x) = ((.(an(x – xn – 1) + an – 1)(x – xn – 2) + .)(x – x1) + a1)*
*(x – x0) + a0. (6)
Теперь рассмотрим, как находятся постоянные a в формуле Ньютона. Их можно
определить, находя «разделённые разности» и сводя вычисления в следующую
таблицу (иллюстрирующую случай n = 3):
y0
(y1 – y0)/(x1 – x0) = y¢1
y1 (y2 – y’1)/(x2 – x0) = y¢¢2
(y2 – y1)/(x2 – x
1) = y¢2 (
y’’3 – y’’2)/(x3 – x
0) = y¢¢¢3
y2 (y3 – y’2)/(x3 – x1) = y¢¢3
(y3 – y2)/(x3 – x2) = y¢3
y3
(7)
Можно доказать, что a0 = y0, a1 =
y’1, a2 = y’2, и т. д.
Следовательно, для нахождения величин может быть использована следующая
вычислительная процедура (соответствующая таблице (7)):
Начать с того, что установить (a0, a1, ., an
) ¬ (y0, y1, . , yn);
затем для k = 1, 2, ., n (именно в таком порядке) установить
yj ¬ (yj – yj –
1)/(xj – xj – k
) для j = n, n – 1, ., k (именно в таком
порядке).
Если мы хотим вычислить многочлен u(x) степени n сразу
для многих значений x, образующих арифметическую прогрессию (т. е.
хотим вычислить u(x0), u(x0
+ h), u(x0 + 2h),.), то весь процесс
можно после нескольких первых шагов свести к одному только сложению вследствие
того факта, что n-я разность от многочлена есть постоянная.
1 Найти коэффициенты bn, ., b1, b0
представления нашего многочлена в виде интерполяционного многочлена Ньютона
u(x) = bn / n! hn(
x – x0 – (n – 1)h).(x – x
0 – h)(x – x0) +.+ b2 / 2!
h2* *(x – x0 – h)(x –
x0) + b1 / h2 (x – x
0) + b0. (8)
(Это можно сделать, беря повторные разности, в точности так же, как мы
определяли выше постоянные a в (5) (надо принять xj = x
0 + jh), с тем исключением, что все деления на xj
– xj – k из вычислительной процедуры
устраняются.)
2 Установить x ¬ x0.
3 Теперь значением u(x) является b0.
4 Установить bj ¬ bj + bj
+ 1 для j = 0, 1, ., n – 1 (именно в таком порядке).
Увеличить x на h и вернуться в шаг 3. M(2l) = 3M(2l – 1),., M(2) = 3M(1), M(1) = 1,
A(2l) = 3A(2l – 1) + 3*2l,., A(2) = 3A(1) + 6, A(1) = 1.
В этой последней формуле член 3*2l представляет собой число
элементарных сложений, необходимых, чтобы сделать два сложения многочленов
степени 2l – 1 – 1 (a + b и c +
d) и два вычитания многочленов степени 2l – 1 (U –
V – W). Суммируя каждое из этих выражений, находим для n,
являющегося степенью двойки:
M(n) = nlog3/log2 » n1,585 и A(2) =7 nlog3/log2 – 6n.
К сожалению, этот принцип остаётся теоретическим, и на его основе нужно
построить итерационный алгоритм, чтобы получить разумную эффективность (цена
управления рекурсией очень велика).
3.4 Вычисление многочленов
Рассмотрим общую задачу вычисления многочлена n-й степени
u(x) = unxn + un –
1xn – 1 + ... + u1x
+ u0, un ¹ 0,
(1)
3.4.1 Схема Горнера
u(x) = (.(unx + un – 1)x + .)x + u0. (2)
Весь этот процесс требует n умножений и n сложений.
Было предложено несколько обобщений схемы Горнера. Посмотрим сначала, как
вычисляется в случае, когда – комплексное число, а коэффициенты вещественны.
Комплексное сложение и умножение можно очевидным образом свести к
последовательности обычных операций над вещественными числами:
вещественное + комплексное требует 1 сложение,
комплексное + комплексное требует 2 сложения,
вещественное * комплексное требует 2 умножения,
комплексное * комплексное требует 4 умножения и 2 сложения
или 3 умножения и 5 сложений.
Следовательно, схема Горнера (2) требует 4n – 2 умножений и 3n – 2
сложений или 3n – 1 умножений и 6n – 5 сложений для вычисления
u(z), когда z комплексное. Вот другая процедура для
вычисления u(x + iy):
a1 = un, b1 = un – 1, r = x + x, s = x2 + y2; (3)
aj = bj – 1 + raj –1, bj = un – j – saj –1, 1 < j £ n.
Легко доказать индукцией по n, что u(z) = zan
+ bn. Эта схема требует 2n + 2 умножений и 2n +
1 сложений, так что при n ³ 3 она лучше схемы Горнера.
Рассмотрим процесс деления многочлена u(x) на многочлен x – x
0. В результате такого деления мы получаем u(x) = (x
– x0)q(x) + r(x); здесь deg(r
) < 1, поэтому r(x) есть постоянная, не зависящая от x
и u(x0) = 0*q(x0) + r
= r. Анализ этого процесса деления показывает, что вычисления почти те
же самые, что в схеме Горнера для определения u(x0).
Аналогично, когда мы делим u(z) на многочлен (z – z
0)(z – z0) = z2 – 2x
0z + x02 + y0
2, то соответствующие вычисления эквивалентны процедуре (3); мы получаем
u(z) = (z – z0)(z – z0)q(z) + anz + bn;
следовательно,
u(z0) = anz0 + bn.
Вообще, когда мы делим u(x) на, f(x) получая u
(x) = f(x) q(x) + r(x), то
из равенства f(x0) = 0 следует u(x
0) = r(x0); это наблюдение ведёт к дальнейшим
обобщениям правила Горнера. Мы можем положить, например, f(x) =
x2 – x02; это даст нам схему
Горнера «второго порядка»
u(x) = (.(u2ë n/2 û x2 + u2ë n/2 û – 2)x2 + u0 +
+((..u2é n/2
ù - 1 x2 + u2
é n/2 ù - 3
)x2 + . +)x2u1) x.
(4)
3.4.2 Интерполяционная формула Ньютона и табулирование значений многочлена
Рассмотрим специальный случай вычисления многочлена. Интерполяционный многочлен
Ньютона степени n, определяемый формулой
u[n](x) = an(x – x
0) (x – x1).(x – xn
– 1) +.+ an (x – x0) (x
– x1) + a1 (x – x0) + a
0, (5)
является единственным многочленом степени £ n от x,
который принимает предписанные значения y0, y1
, ., yn в заданных n + 1 различных точках x
0, x1, ., xn соответственно. После
того, как значения постоянных a найдены, интерполяционная формула Ньютона
становится удобной для вычислений, так как мы можем, обобщив правило Горнера,
записать
u[n](x) = ((.(an(x – xn – 1) + an – 1)(x – xn – 2) + .)(x – x1) + a1)*
*(x – x0) + a0. (6)
Теперь рассмотрим, как находятся постоянные a в формуле Ньютона. Их можно
определить, находя «разделённые разности» и сводя вычисления в следующую
таблицу (иллюстрирующую случай n = 3):
y0
(y1 – y0)/(x1 – x0) = y¢1
y1 (y2 – y’1)/(x2 – x0) = y¢¢2
(y2 – y1)/(x2 – x
1) = y¢2 (
y’’3 – y’’2)/(x3 – x
0) = y¢¢¢3
y2 (y3 – y’2)/(x3 – x1) = y¢¢3
(y3 – y2)/(x3 – x2) = y¢3
y3
(7)
Можно доказать, что a0 = y0, a1 =
y’1, a2 = y’2, и т. д.
Следовательно, для нахождения величин может быть использована следующая
вычислительная процедура (соответствующая таблице (7)):
Начать с того, что установить (a0, a1, ., an
) ¬ (y0, y1, . , yn);
затем для k = 1, 2, ., n (именно в таком порядке) установить
yj ¬ (yj – yj –
1)/(xj – xj – k
) для j = n, n – 1, ., k (именно в таком
порядке).
Если мы хотим вычислить многочлен u(x) степени n сразу
для многих значений x, образующих арифметическую прогрессию (т. е.
хотим вычислить u(x0), u(x0
+ h), u(x0 + 2h),.), то весь процесс
можно после нескольких первых шагов свести к одному только сложению вследствие
того факта, что n-я разность от многочлена есть постоянная.
1 Найти коэффициенты bn, ., b1, b0
представления нашего многочлена в виде интерполяционного многочлена Ньютона
u(x) = bn / n! hn(
x – x0 – (n – 1)h).(x – x
0 – h)(x – x0) +.+ b2 / 2!
h2* *(x – x0 – h)(x –
x0) + b1 / h2 (x – x
0) + b0. (8)
(Это можно сделать, беря повторные разности, в точности так же, как мы
определяли выше постоянные a в (5) (надо принять xj = x
0 + jh), с тем исключением, что все деления на xj
– xj – k из вычислительной процедуры
устраняются.)
2 Установить x ¬ x0.
3 Теперь значением u(x) является b0.
4 Установить bj ¬ bj + bj
+ 1 для j = 0, 1, ., n – 1 (именно в таком порядке).
Увеличить x на h и вернуться в шаг 3.
4. Дискретное логарифмирование
Пусть p – простое число. Ещё Эйлер знал, что мультипликативная группа
кольца циклична, т. е. существуют такие целые числа а, что сравнение
ax º b (mod p) (2)
разрешимо относительно x при любом bÎZ, не делящимся на
p. Числа а с этим свойством называются первообразными корнями, и
количество их равно j(p – 1), где j – функция Эйлера. Целое х,
удовлетворяющее сравнению (2), называется индексом или дискретным логарифмом
числа b.
Выше мы описали алгоритм, позволяющий по заданному числу x достаточно
быстро вычислять ах mod p. Обратная же операция –
вычисление по заданному b его дискретного логарифма, вообще говоря,
является очень сложной в вычислительном отношении задачей. Именно это свойство
дискретного логарифма и используется в его многочисленных криптографических
применениях. Наиболее быстрые (из известных) алгоритмы решения этой задачи,
основанные на так называемом методе решета числового поля, требуют выполнения
exp(c(ln p)1/3(ln ln p)2/3)
арифметических операций, где c – некоторая положительная постоянная.
Это сравнимо со сложностью наиболее быстрых алгоритмов разложения чисел на
множители. Конечно, указанная оценка сложности получена при условии
справедливости ряда достаточно правдоподобных гипотез.
Говоря о сложности задачи дискретного логарифмирования, мы имели в виду
«общий случай». Ведь и большое целое число легко может быть разложено на
простые сомножители, если все эти сомножители не очень велики. Известен
алгоритм, позволяющий быстро решать задачу дискретного логарифмирования, если
p – 1 есть произведение малых простых чисел.
Пусть q – простое число, делящее р – 1. Обозначим с
º а(p – 1)/q
(mod p), тогда классы вычетов 1, с, с2, . ,
сq – 1 все различны и образуют полное множество
решений уравнения хq = 1 в поле Fp = Z/Z
p. Если q не велико и целое число d удовлетворяет
сравнению хq º 1 (mod p), то показатель k
, 0 £ k < q, для которого выполняется d º
ck (mod p), легко может быть найден, например, с помощью
перебора. Именно на этом свойстве основан упомянутый выше алгоритм.
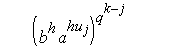 Допустим, что р – 1 =
qkh, (q,h) = 1. Алгоритм последовательно строит
целые числа uj, j = 0,1,.,k, для которых
выполняется сравнение Допустим, что р – 1 =
qkh, (q,h) = 1. Алгоритм последовательно строит
целые числа uj, j = 0,1,.,k, для которых
выполняется сравнение
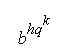 º 1 (mod p). (3)
º 1 (mod p). (3)
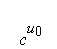 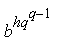 Так как выполняется сравнение º 1 (mod p), то найдётся
целое число u0, для которого º (mod
p). При таком выборе сравнение (3) с j = 0, очевидно, выполняется.
Предположим, что найдено число uj, удовлетворяющее сравнению
(3). Тогда определим t с помощью сравнения
Так как выполняется сравнение º 1 (mod p), то найдётся
целое число u0, для которого º (mod
p). При таком выборе сравнение (3) с j = 0, очевидно, выполняется.
Предположим, что найдено число uj, удовлетворяющее сравнению
(3). Тогда определим t с помощью сравнения
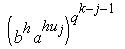 º ct (mod p), (4)
º ct (mod p), (4)
 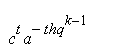 и положим. Имеют место сравнения
º º 1 (mod p), (5) и положим. Имеют место сравнения
º º 1 (mod p), (5)
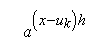 означающие справедливость (3) при j + 1.
При j = k сравнение означает в силу (2), что º
1 (mod p). Целое число а есть первообразный корень по модулю
р, поэтому имеем (x – uk)h º 0 (mod
p – 1) и означающие справедливость (3) при j + 1.
При j = k сравнение означает в силу (2), что º
1 (mod p). Целое число а есть первообразный корень по модулю
р, поэтому имеем (x – uk)h º 0 (mod
p – 1) и
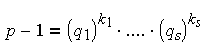 x º uk (mod qk). x º uk (mod qk).
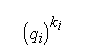 Если
, где все простые числа qj
малы, то указанная процедура позволяет найти вычеты x mod , i
= 1,.,s, и, с помощью китайской теоремы об остатках, вычет x mod
p – 1, т. е. решить сравнение (2).
В случае обычных логарифмов в поле действительных чисел имеется специальное
основание e = 2,171828., позволяющее достаточно быстро вычислять логарифмы с
произвольной точностью. Например, это можно делать с помощью быстро
сходящегося ряда
ln(1+x)/(1 – x) = 2(x + x3/3 + x5/5 + .), |x| < 1. (6)
Логарифмы по произвольному основанию с могут быть вычислены с помощью тождества
logc x = ln x/ ln c. (7)
В случае дискретных логарифмов нет основания, по которому логарифмы вычислялись
бы столь же быстро, как натуральные в поле действительных чисел. Вместе с тем,
последняя формула, связывающая логарифмы с различными основаниями, остаётся
справедливой и позволяет выбирать основание удобным способом. Единственное
условие для этого состоит в том, чтобы логарифм нового основания Log c
был взаимно прост c p - 1. Тогда в формуле (7) возможно деление по
модулю р – 1. Заметим, что это условие будет выполнено, если и только
если с – первообразный корень. Из расширенной гипотезы Римана следует,
что наименьший первообразный корень по модулю р ограничен величиной
O(log6 p). Поэтому в дальнейшем для простоты изложения мы
будем предполагать, что основание а в (2) невелико, именно а =
O(log6 p). Если
, где все простые числа qj
малы, то указанная процедура позволяет найти вычеты x mod , i
= 1,.,s, и, с помощью китайской теоремы об остатках, вычет x mod
p – 1, т. е. решить сравнение (2).
В случае обычных логарифмов в поле действительных чисел имеется специальное
основание e = 2,171828., позволяющее достаточно быстро вычислять логарифмы с
произвольной точностью. Например, это можно делать с помощью быстро
сходящегося ряда
ln(1+x)/(1 – x) = 2(x + x3/3 + x5/5 + .), |x| < 1. (6)
Логарифмы по произвольному основанию с могут быть вычислены с помощью тождества
logc x = ln x/ ln c. (7)
В случае дискретных логарифмов нет основания, по которому логарифмы вычислялись
бы столь же быстро, как натуральные в поле действительных чисел. Вместе с тем,
последняя формула, связывающая логарифмы с различными основаниями, остаётся
справедливой и позволяет выбирать основание удобным способом. Единственное
условие для этого состоит в том, чтобы логарифм нового основания Log c
был взаимно прост c p - 1. Тогда в формуле (7) возможно деление по
модулю р – 1. Заметим, что это условие будет выполнено, если и только
если с – первообразный корень. Из расширенной гипотезы Римана следует,
что наименьший первообразный корень по модулю р ограничен величиной
O(log6 p). Поэтому в дальнейшем для простоты изложения мы
будем предполагать, что основание а в (2) невелико, именно а =
O(log6 p).
 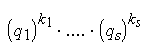 Так как поле Fp неполно, вычисление дискретных логарифмов не может
использовать предельный переход и основано на иных принципах. Прежде всего,
нужный дискретный логарифм log b вычисляется не сам по себе, а вместе с
совокупностью логарифмов ряда других чисел. Заметим, что всякое сравнение вида
º (mod p), (8)
где qi, ki, mi Î Z приводит к соотношению между логарифмами
(k1 – m1)Log q1 + . + (ks – ms)Log qs º 0 (mod p – 1). (9)
Так как поле Fp неполно, вычисление дискретных логарифмов не может
использовать предельный переход и основано на иных принципах. Прежде всего,
нужный дискретный логарифм log b вычисляется не сам по себе, а вместе с
совокупностью логарифмов ряда других чисел. Заметим, что всякое сравнение вида
º (mod p), (8)
где qi, ki, mi Î Z приводит к соотношению между логарифмами
(k1 – m1)Log q1 + . + (ks – ms)Log qs º 0 (mod p – 1). (9)
  А если выполняются сравнения
А если выполняются сравнения
a º
(mod p – 1) b º
(mod p), то
r1Log q1 +.+ rsLog qs º 1 (mod p – 1) (10)
и
Log b º x1Log q1 +.+ xsLog qs (mod p – 1) (11)
Имея достаточно много векторов k1,.,ks,
m1,.,ms с условием (8), можно найти решение
соответствующей системы сравнений (9), (10). Если эта система имеет
единственное решение, то им как раз и будет набор логарифмов Log q
1,.,Log qs. Затем с помощью (11) можно найти Log b
.
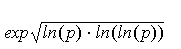 Мы опишем ниже реализацию этой
идеи, взятую из работы [1]. Эвристические соображения позволили авторам этой
работы утверждать, что предложенный ими алгоритм требует L1 + e
, где L = , арифметических операций для вычисления
Log b. Мы опишем ниже реализацию этой
идеи, взятую из работы [1]. Эвристические соображения позволили авторам этой
работы утверждать, что предложенный ими алгоритм требует L1 + e
, где L = , арифметических операций для вычисления
Log b.
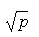 Положим Положим
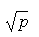 H = [ ] + 1, J = H2 – q.
Тогда 0 < J < 2 + 1, и, как легко проверить, для любой пары целых
чисел с1, с2 выполняется сравнение
(H + c1) (H + c2) º J + (c1 + c2)H + c1c2 (mod p). (12)
Если числа ci не очень велики, скажем ci
£ L1/2 + e при некотором e > 0, то правая часть
сравнения (12) не превосходит p1/2 + e/2
. Можно доказать, что случайно выбранное натуральное число x < p
1/2 + e/2 раскладывается в произведение простых
чисел, меньших с вероятностью, большей, чем L-1/2 - e
/2.
Обозначим через S = {q1,.,qs} совокупность
всех простых чисел q < L1/2, а также всех простых чисел
вида H + c при 0 < c < L1/2 + e.
Тогда s = O(L1/2 + e). Будем теперь
перебирать случайным образом числа и для каждой такой пары пытаться разложить
на множители соответствующее выражение из правой части (12). Для разложения
можно воспользоваться, например, делением на все простые числа, меньшие, чем L
1/2. Перебрав все (L1/2 + e )2/2 = O
(L1 + 2e ) указанных пар с1, с
2 мы найдём, как это следует из указанных выше вероятностных соображений,
не менее
L-1/2 - e/2 *O(L1 + 2e
) = O(L1/2 + 3e/2)
(13)
пар, для которых правая часть сравнения (12) полностью раскладывается на простые
сомножители, меньшие L1/2. Сравнение (12), таким образом, принимает
вид (8). Так строится система уравнений типа (9).
Напомним, что число а, согласно нашему предположению, существенно
меньше, чем L1/2. Поэтому оно раскладывается в произведение простых
чисел, входящих во множество {q1,.,qs}, и
это приводит к сравнению (10).
Заметим, что количество (13) найденных сравнений типа (9) превосходит число
s. Следовательно, построенная система неоднородных линейных сравнений
относительно Log qi содержит сравнений больше, чем
неизвестных. Конечно, множество её решений может при этом быть бесконечным.
Одна из правдоподобных гипотез состоит в том, что система имеет всё-таки
единственное решение, и, решив её, можно определить дискретные логарифмы всех
чисел qi. На этом завершается первый этап работы алгоритма
из [1].
Как было отмечено, каждое из чисел, стоящих в правой части сравнения (12), не
превосходит p1/2 + e/2. Поэтому оно
раскладывается в произведение не более O(ln p) простых
сомножителей и, следовательно, каждое из сравнений (9) построенной системы
содержит лишь O(ln p) отличных от нуля коэффициентов. Матрица
системы сравнений будет разреженной, что позволяет применять для её решения
специальные методы с меньшей оценкой сложности, чем обычный гауссов метод
исключения переменных.
Вместо перебора всех допустимых значений ci в [1]
предлагается использовать так называемое решето, отбрасывающее все пары этих
чисел, для которых правая часть (12) заведомо не раскладывается в произведение
малых простых сомножителей. Для каждого c1 и каждой малой
простой степени q' < L1/2 можно найти все решения c
2 < L1/2 линейного сравнения
J + (c1 + c2)H + c1c2 º 0 (mod q').
Организованная правильным образом, эта процедура одновременно отбирает все
нужные пары чисел c1,c2 и даёт разложение
на простые сомножители правых частей сравнений (12). H = [ ] + 1, J = H2 – q.
Тогда 0 < J < 2 + 1, и, как легко проверить, для любой пары целых
чисел с1, с2 выполняется сравнение
(H + c1) (H + c2) º J + (c1 + c2)H + c1c2 (mod p). (12)
Если числа ci не очень велики, скажем ci
£ L1/2 + e при некотором e > 0, то правая часть
сравнения (12) не превосходит p1/2 + e/2
. Можно доказать, что случайно выбранное натуральное число x < p
1/2 + e/2 раскладывается в произведение простых
чисел, меньших с вероятностью, большей, чем L-1/2 - e
/2.
Обозначим через S = {q1,.,qs} совокупность
всех простых чисел q < L1/2, а также всех простых чисел
вида H + c при 0 < c < L1/2 + e.
Тогда s = O(L1/2 + e). Будем теперь
перебирать случайным образом числа и для каждой такой пары пытаться разложить
на множители соответствующее выражение из правой части (12). Для разложения
можно воспользоваться, например, делением на все простые числа, меньшие, чем L
1/2. Перебрав все (L1/2 + e )2/2 = O
(L1 + 2e ) указанных пар с1, с
2 мы найдём, как это следует из указанных выше вероятностных соображений,
не менее
L-1/2 - e/2 *O(L1 + 2e
) = O(L1/2 + 3e/2)
(13)
пар, для которых правая часть сравнения (12) полностью раскладывается на простые
сомножители, меньшие L1/2. Сравнение (12), таким образом, принимает
вид (8). Так строится система уравнений типа (9).
Напомним, что число а, согласно нашему предположению, существенно
меньше, чем L1/2. Поэтому оно раскладывается в произведение простых
чисел, входящих во множество {q1,.,qs}, и
это приводит к сравнению (10).
Заметим, что количество (13) найденных сравнений типа (9) превосходит число
s. Следовательно, построенная система неоднородных линейных сравнений
относительно Log qi содержит сравнений больше, чем
неизвестных. Конечно, множество её решений может при этом быть бесконечным.
Одна из правдоподобных гипотез состоит в том, что система имеет всё-таки
единственное решение, и, решив её, можно определить дискретные логарифмы всех
чисел qi. На этом завершается первый этап работы алгоритма
из [1].
Как было отмечено, каждое из чисел, стоящих в правой части сравнения (12), не
превосходит p1/2 + e/2. Поэтому оно
раскладывается в произведение не более O(ln p) простых
сомножителей и, следовательно, каждое из сравнений (9) построенной системы
содержит лишь O(ln p) отличных от нуля коэффициентов. Матрица
системы сравнений будет разреженной, что позволяет применять для её решения
специальные методы с меньшей оценкой сложности, чем обычный гауссов метод
исключения переменных.
Вместо перебора всех допустимых значений ci в [1]
предлагается использовать так называемое решето, отбрасывающее все пары этих
чисел, для которых правая часть (12) заведомо не раскладывается в произведение
малых простых сомножителей. Для каждого c1 и каждой малой
простой степени q' < L1/2 можно найти все решения c
2 < L1/2 линейного сравнения
J + (c1 + c2)H + c1c2 º 0 (mod q').
Организованная правильным образом, эта процедура одновременно отбирает все
нужные пары чисел c1,c2 и даёт разложение
на простые сомножители правых частей сравнений (12).
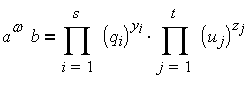 Итак, после первого этапа
работы алгоритма в нашем распоряжении оказываются дискретные логарифмы всех
чисел из множества S. Второй этап алгоритма сводит поиск дискретного логарифма
числа b к поиску логарифмов некоторого множества чисел u, не
превосходящих по величине L2. Выбирая случайным образом
число w не более L1/4 раз, можно, как показывают
вероятностные соображения, найти такое w, что вычет awb
mod p раскладывается в произведение простых чисел, меньших L
2. Пусть
(mod p)
такое разложение, где u1,.,ut – некоторые
простые числа с условием L1/2 < u < <
L2. На поиск этого сравнения потребуется O(L1/2
)арифметических операций. В результате вычисление дискретного логарифма числа
b сводится к вычислению t дискретных логарифмов для чисел u
j, 1 £ j £ t среднего размера.
Наконец, на последнем этапе производится вычисление логарифмов всех чисел u
j. Пусть u – простое число из интервала условием L
1/2 < u < L2. Обозначим
G = [Öp / u], I = HGu – p.
Для любых целых чисел c1, c2 < L1/2 + e выполняется сравнение
(H + c1) (H + c2)u
º I + (c1G+ c2H + c
1c2 )u (mod p).
(14)
Отметим, что правая часть этого сравнения не превосходит p1/2
L5/2 + e. Просеивая все числа c1,
c2 из указанного интервала, можно найти такие, что числа G+ c
2 и правая часть сравнения (14) состоят из простых сомножителей, не
превосходящих L1/2. Тогда сравнение (14) позволяет вычислить
Log u. Вычисление Log b при известных уже значениях Log q
1 требует L1/2 + e арифметических
операций.
Существуют и другие способы построения соотношений (8). В [2] для этого
используются вычисления в полях алгебраических чисел. В качестве множителей в
соотношения типа (8) используются не только простые числа, но и простые
идеалы с небольшой нормой.
Задача вычисления дискретных логарифмов может рассматриваться также и в полях F
pn, состоящих из pn элементов, в
мультипликативных группах классов вычетов (Z/mZ)*, в группах точек
эллиптических кривых и вообще в произвольных группах.
Список литературы
1. Введение в криптографию под общей редакцией Ященко, М.: МЦНМО:
«Черо», 1999.
2. Алгебраическая алгоритмика, Ноден П., Китте К., М.: «Мир», 1999.
[1] Coppersmith D., Odlyzko A. M., Schroeppel R. Descrete logarithms
in GF(p) // Algorithmica. V. 1,1986. P. 1-15.
[2] Lenstra A. K, Lenstra H. W. (jr.) The Development of the
Number Field Siev. Lect. Notes in Math. V. 1554. Springer, 1993.
[3] McCarthy D. P. “The optimal algorithm to evaluate x
n using elementary multiplication methods”, Math. Comp
., vol. 31, no 137, 1977, pp. 251 – 256. Итак, после первого этапа
работы алгоритма в нашем распоряжении оказываются дискретные логарифмы всех
чисел из множества S. Второй этап алгоритма сводит поиск дискретного логарифма
числа b к поиску логарифмов некоторого множества чисел u, не
превосходящих по величине L2. Выбирая случайным образом
число w не более L1/4 раз, можно, как показывают
вероятностные соображения, найти такое w, что вычет awb
mod p раскладывается в произведение простых чисел, меньших L
2. Пусть
(mod p)
такое разложение, где u1,.,ut – некоторые
простые числа с условием L1/2 < u < <
L2. На поиск этого сравнения потребуется O(L1/2
)арифметических операций. В результате вычисление дискретного логарифма числа
b сводится к вычислению t дискретных логарифмов для чисел u
j, 1 £ j £ t среднего размера.
Наконец, на последнем этапе производится вычисление логарифмов всех чисел u
j. Пусть u – простое число из интервала условием L
1/2 < u < L2. Обозначим
G = [Öp / u], I = HGu – p.
Для любых целых чисел c1, c2 < L1/2 + e выполняется сравнение
(H + c1) (H + c2)u
º I + (c1G+ c2H + c
1c2 )u (mod p).
(14)
Отметим, что правая часть этого сравнения не превосходит p1/2
L5/2 + e. Просеивая все числа c1,
c2 из указанного интервала, можно найти такие, что числа G+ c
2 и правая часть сравнения (14) состоят из простых сомножителей, не
превосходящих L1/2. Тогда сравнение (14) позволяет вычислить
Log u. Вычисление Log b при известных уже значениях Log q
1 требует L1/2 + e арифметических
операций.
Существуют и другие способы построения соотношений (8). В [2] для этого
используются вычисления в полях алгебраических чисел. В качестве множителей в
соотношения типа (8) используются не только простые числа, но и простые
идеалы с небольшой нормой.
Задача вычисления дискретных логарифмов может рассматриваться также и в полях F
pn, состоящих из pn элементов, в
мультипликативных группах классов вычетов (Z/mZ)*, в группах точек
эллиптических кривых и вообще в произвольных группах.
Список литературы
1. Введение в криптографию под общей редакцией Ященко, М.: МЦНМО:
«Черо», 1999.
2. Алгебраическая алгоритмика, Ноден П., Китте К., М.: «Мир», 1999.
[1] Coppersmith D., Odlyzko A. M., Schroeppel R. Descrete logarithms
in GF(p) // Algorithmica. V. 1,1986. P. 1-15.
[2] Lenstra A. K, Lenstra H. W. (jr.) The Development of the
Number Field Siev. Lect. Notes in Math. V. 1554. Springer, 1993.
[3] McCarthy D. P. “The optimal algorithm to evaluate x
n using elementary multiplication methods”, Math. Comp
., vol. 31, no 137, 1977, pp. 251 – 256.
Страницы: 1, 2
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



