|
Доказательство.
Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.
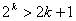 . (1) . (1)
Докажем, что тогда неравенство справедливо и при n=k+1, т.е.
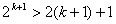 . .
Действительно, 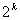 не не
меньше 2 при любом натуральном k. Прибавим к левой части неравенства (1) 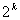
, а к правой 2. Получим справедливое неравенство 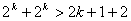
, или 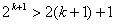 . Утверждение . Утверждение
доказано.
Пример 3. Доказать, что 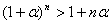 , где , где 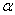 >-1, >-1, 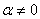 , n – натуральное число, большее 1. , n – натуральное число, большее 1.
Решение.
При n=2 неравенство справедливо, так как 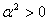 . .
Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.
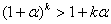 . (1) . (1)
Покажем, что тогда неравенство справедливо и при n=k+1, т.е.
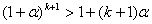 . (2) . (2)
Действительно, по условию, 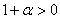 , поэтому справедливо неравенство , поэтому справедливо неравенство
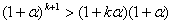 , (3) , (3)
полученное из неравенства (1) умножением каждой части его на 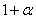
. Перепишем неравенство (3) так: 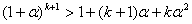
. Отбросив в правой части последнего неравенства положительное слагаемое 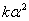
, получим справедливое неравенство (2).
Пример 4. Доказать, что
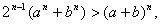 (1) (1)
где 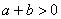 , , 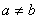 , n – натуральное число, большее 1. , n – натуральное число, большее 1.
Решение.
При n=2 неравенство (1) принимает вид
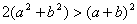 . (2) . (2)
Так как 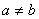 , то справедливо неравенство , то справедливо неравенство
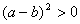 . (3) . (3)
Прибавив к каждой части неравенства (3) по 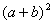 , получим неравенство (2). , получим неравенство (2).
Этим доказано, что при n=2 неравенство (1) справедливо.
Пусть неравенство (1) справедливо при n=k, где k – некоторое натуральное
число, т.е.
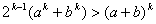 . (4) . (4)
Докажем, что тогда неравенство (1) должно быть справедливо и при n=k+1, т.е.
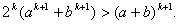 (5) (5)
Умножим обе части неравенства (4) на a+b. Так как, по условию, 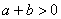
, то получаем следующее справедливое неравенство:
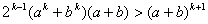 . (6) . (6)
Для того чтобы доказать справедливость неравенства (5), достаточно показать, что
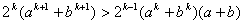 , (7) , (7)
или, что то же самое,
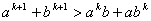 . (8) . (8)
Неравенство (8) равносильно неравенству
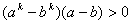 . (9) . (9)
Если 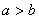 , то , то 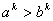
, и в левой части неравенства (9) имеем произведение двух положительных чисел.
Если 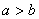 , то , то 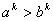
, и в левой части неравенства (9) имеем произведение двух отрицательных чисел. В
обоих случаях неравенство (9) справедливо.
Этим доказано, что из справедливости неравенства (1) при n=k следует его
справедливость при n=k+1.
Метод математической индукции в решении задач на делимость.
С помощью метода математической индукции можно доказывать различные
утверждения, касающиеся делимости натуральных чисел.
Следующее утверждение можно сравнительно просто доказать. Покажем, как оно
получается с помощью метода математической индукции.
Пример 1. Если n – натуральное число, то число 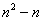 четное. четное.
 При n=1 наше При n=1 наше
утверждение истинно: 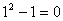
- четное число. Предположим, что 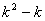
- четное число. Так как 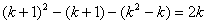
, a 2k – четное число, то и 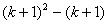
четное. Итак, четность 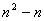
доказана при n=1, из четности 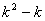
выведена четность 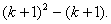
.Значит, 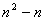 четно при четно при
всех натуральных значениях n.
Пример 2. Доказать истинность предложения
A(n)={число 5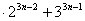 кратно 19}, n – натуральное число. кратно 19}, n – натуральное число.
Решение.
Высказывание А(1)={число 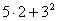 кратно 19} истинно. кратно 19} истинно.
Предположим, что для некоторого значения n=k
А(k)={число 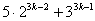 кратно 19} истинно. Тогда, так как кратно 19} истинно. Тогда, так как
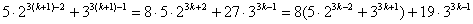
, очевидно, что и A(k+1) истинно. Действительно, первое слагаемое делится
на 19 в силу предположения, что A(k) истинно; второе слагаемое тоже делится на
19, потому что содержит множитель 19. Оба условия принципа математической
индукции выполнены, следовательно, предложение A(n) истинно при всех значениях
n.
Доказательство тождеств с помощью метода математической индукции
Доказать , что при всех допустимых значениях x имеет место тождество:
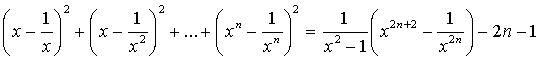
Решение. Надо доказать , что тождество справедливо при всех x , кроме
x=0, 1, -1.
При n=1 имеем:
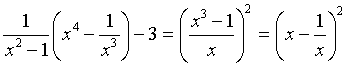 , ,
т.е. при n=1 тождество выполняется.
Предположим , что
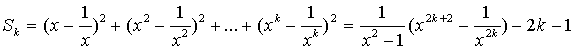
Докажем , что тогда
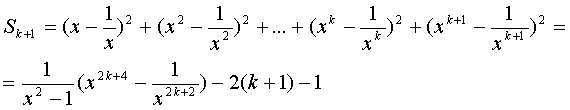
Имеем:
Итак, тождество верно для любого натурального числа n.
Метод математической индукции в применение к другим задачам.
Наиболее естественное применение метода математической индукции в геометрии,
близкое к использованию этого метода в теории чисел и в алгебре, - это
применение к решению геометрических задач на вычисление. Рассмотрим несколько
примеров.
Пример 1. Вычислить сторону 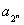
правильного 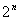 - -
угольника, вписанного в круг радиуса R.
Решение.
При n=2 правильный 2n – угольник есть квадрат; его сторона 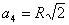
. Далее, согласно формуле удвоения
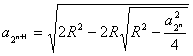
находим, что сторона правильного восьмиугольника 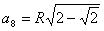
, сторона правильного шестнадцатиугольника 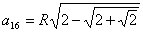
, сторона правильного тридцатидвухугольника 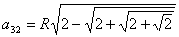
. Можно предположить поэтому, что сторона правильного вписанного 2n –
угольника при любом 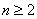
равна
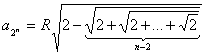 . (1) . (1)
Допустим, что сторона правильного вписанного 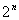
- угольника выражается формулой (1). В таком случае по формуле удвоения
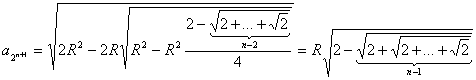
,
откуда следует, что формула (1) справедлива при всех n.
Пример 2. На сколько треугольников n-угольник (не обязательно выпуклый)
может быть разбит своими непересекающимися диагоналями?
Решение.
Для треугольника это число равно единице (в треугольнике нельзя провести ни
одной диагонали); для четырехугольника это число равно, очевидно, двум.
Предположим, что мы уже знаем, что каждый k-угольник, где k<n, разбивается
непересекающимися диагоналями на k-2 треугольника (независимо от способа
разбиения). Рассмотрим одно из разбиений n-угольника А1А2
.Аn на треугольники.
  Аn Аn
А1 А2
Пусть А1Аk – одна из диагоналей этого разбиения; она
делит n-угольник А1А2.Аn на k-угольник A1
A2.Ak и (n-k+2)-угольник А1АkAk
+1.An. В силу сделанного предположения, общее число
треугольников разбиения будет равно
(k-2)+[(n-k+2)-2]=n-2;
тем самым наше утверждение доказано для всех n.
Пример 3. Указать правило вычисления числа P(n) способов, которыми
выпуклый n-угольник может быть разбит на треугольники непересекающимися
диагоналями.
Решение.
Для треугольника это число равно, очевидно, единице: P(3)=1.
Предположим, что мы уже определили числа P(k) для всех k<n; найдем, чему
равно в таком случае P(n). Для этого рассмотрим выпуклый n-угольник А1
А2.Аn. При всяком разбиении его на треугольники сторона А
1А2 будет стороной одного из треугольников разбиения, третья
вершина этого треугольника может совпасть с каждой из точек А3, А
4, .,Аn. Число способов разбиения n-угольника, при которых эта
вершина совпадает с точкой А3, равно числу способов разбиения на
треугольники (n-1)-угольника А1А3А4.Аn
, т.е. равно P(n-1). Число способов разбиения, при которых эта вершина совпадает
с А4, равно числу способов разбиения (n-2)-угольника А1А
4А5.Аn, т.е. равно P(n-2)=P(n-2)P(3); число способов
разбиения, при которых она совпадает с А5, равно P(n-3)P(4), так как
каждое из разбиений (n-3)-угольника А1А5.Аn
можно комбинировать при этом с каждым из разбиений четырехугольника А2
А3А4А5, и т.д. Таким образом, мы приходим к
следующему соотношению:
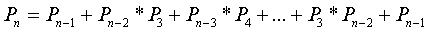
С помощью этой формулы последовательно получаем:
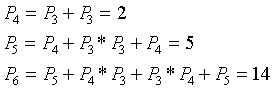
и т.д.
Так же при помощи метода математической индукции можно решать задачи с графами.
Пусть на плоскости задана сеть линий, соединяющих между собой какие-то точки и
не имеющие других точек. Такую сеть линий мы будем называть картой,
заданные точки ее вершинами, отрезки кривых между двумя смежными
вершинами – границами карты, части плоскости, на которые она
разбивается границами – странами карты.
Пусть на плоскости задана некоторая карта. Мы будем говорить, что она
правильно раскрашена, если каждая ее страна закрашена определенной краской,
причем любые две страны, имеющие между собой общую границу, закрашены в разные
цвета.
Пример 4. На плоскости дано n окружностей. Доказать, что при любом
расположении этих окружностей образуемую ими карту можно правильно раскрасить
двумя красками.
Решение.
При n=1 наше утверждение очевидно.
Предположим, что наше утверждение справедливо для любой карты, образованной n
окружностями, и пусть на плоскости задано n+1 окружностей. Удалив одну из
этих окружностей, мы получим карту, которую в силу сделанного предположения
можно правильно раскрасить двумя красками, например черной и белой.
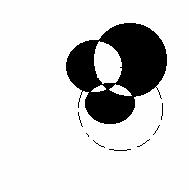 
Восстановим затем отброшенную окружность и по одну сторону от нее (например,
внутри) изменим цвет каждой области на противоположный (т.е. черный – на белый
и наоборот); легко видеть, что при этом мы получим карту, правильную
раскрашенную двумя красками.
Пример 5. Для того чтобы карту можно было правильно раскрасить двумя
красками, необходимо и достаточно, чтобы в каждой ее вершине сходилось четное
число границ.
Решение.
Необходимость этого условия очевидно, так как если в какой-нибудь вершине
карты сходится нечетное число границ, то уже страны, окружающие эту вершину,
нельзя правильно раскрасить двумя красками.
А В
Для доказательства достаточности условия проведем индукцию по числу границ
карты.
Для карты с двумя границами утверждение очевидно.
Предположим, что утверждение справедливо для любой карты, в каждой вершине
которой сходится четное число границ и общее число границ которой не
превосходит n, и пусть дана карта S, имеющая n+1 границ и удовлетворяющая тому
же условию. Начиная с произвольной вершины А карты S, станем двигаться в
произвольном направлении вдоль границ карты. Ввиду конечности числа вершин
карты мы вернемся в конце концов в одну из уже проведенных вершин (карта не
имеет крайних вершин, потому что на ней нет неразделяющих границ) и сможем
выделить некоторый не имеющий самопересечений замкнутый контур, состоящий из
границ карты. Удалив этот контур, мы получим контур S1 с меньшим
числом границ, в каждой вершине которой также сходится четное число границ
(потому что в каждой вершине карты S отбрасывается четное число границ – 0 или
2). В силу индуктивного предположения карту S1 можно правильно
раскрасить двумя красками.
Восстановив отброшенный контур и изменив все цвета с одной стороны от него
(например, внутри), мы и получим правильную раскраску карты S.
Страницы: 1, 2
| 


