двух ломаных, которые при соединении образуют выпуклую оболочку. Для начала

нужно определить две точки, которые будут являться соседними вершинами выпуклой

оболочки. Можно взять самую левую вершину, пусть это будет b, и самую

левую относительно b из оставшихся, пусть это будет e. После

чего нужно найти точку h максимально удаленную от прямой be.

Все точки, лежащие в треугольнике bel исключаются из дальнейшего

рассмотрения. Остальные точки будут делиться на два подмножества: точки,

которые лежать левее bh и eh, и точки, которые лежат правее и

bh, и eh. Каждое из них содержит ломаные которые в сочетании с e

, b и h дают выпуклую оболочку. С каждым из них проделываем то

же самое. В подмножестве точек S’, лежащих левее bh и eh

выбираем h’, максимально удаленную от eh, которая делит его на

три части. Из них одна выбрасывается, а остальные делятся опять. Это

реализуется рекурсивной процедурой, которая для данного ей множества возвращает

соответствующую часть выпуклой оболочки.

В случае, когда мощность каждого, из подмножеств, на которое делится множество,

не превосходит некоторой константы умноженной на мощность множества, получаем

сложность алгоритма, как и в быстрой сортировке O(N log N

). Но в худшем случае может потребоваться время O(N 2

).

Алгоритмы типа “разделяй и властвуй”.

В данном алгоритме, в отличие от предыдущего, множество S разбивается на

два равномощных подмножества S’ и S’’, а затем рекурсивно

строятся отдельно оболочки для каждого из них и объединяются.

CH(S) = CH(S’ È S’’) = CH(CH(S’) È CH (S’’))

Сложность этого метода состоит в эффективном нахождении слияния двух выпуклых

оболочек. Следующий алгоритм слияния был предложен Шеймосом

[7]:

Пусть у нас есть выпуклые многоугольники P’ и P’’. Нам требуется

найти P – их слияние. Этого берется любая внутренняя точка p

для P’ и проверяется на принадлежность P’’. Если она

принадлежит, то по теореме 4 мы имеем два упорядоченных относительно полярного

угла к p множества. За время равное сумме точек в них мы можем из них

получить один упорядоченный список. После чего, используя обход Грэхема за

такое же время получить требуемый выпуклый многоугольник.

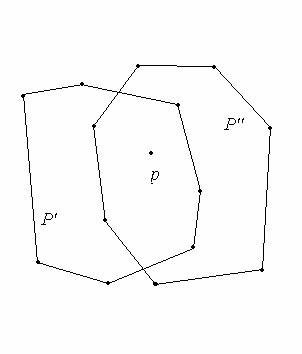
Рис. 2: Так как точка p внутри обоих многоугольников, то вершины, как

одного, так и второго, упорядочены относительно полярного угла к p.

В случае, когда p не принадлежит P’’, придется найти левую и

правую опорные прямые из p к P’’, pl и pr

соответственно. Опорной прямой к выпуклому многоугольнику P

будем называть прямую l, проходящую через некоторую вершину этого

многоугольника, таким образом, что внутренность P находится по одну

сторону от l. Для этого нам достаточно время O(N). Все

вершины P’’ между l и r, при движении от l к

r против часовой стрелки, убираем из рассмотрения и выполняем те действия,

которые выполняли в случае принадлежности.

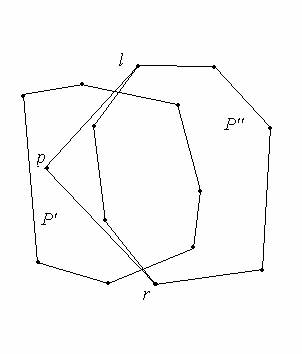
Рис. 3: Так как точка p внутри одного многоугольника, то удаляем все видимые из

p вершины второго многоугольника.

Как видно, и в этом случае на слияние требуется время O(N), где

N – это общее количество точек в многоугольниках. Отсюда следует теорема:

Теорема 6. Выпуклая оболочка объединения двух выпуклых

их вершин.

Динамические алгоритмы построения выпуклой оболочки

Все приведенные алгоритмы не являются открытыми, так как требуют изначально

знать все точки множества S. Но в некоторых случаях требуется иметь

алгоритм способный при поступлении новой точки изменять выпуклую оболочку. В

данном случае мы имеем дело с задачей ВО2.

Очевидно, что решение задачи существует. Можно каждый раз после поступления

точки использовать обход Грэхема и получить алгоритм со сложностью O(

N2 log N), но хотелось бы не приносить в жертву оценку

O(N log N).

Для этого следует обратить внимание на то, что каждую новую точку алгоритм

должен или отбрасывать, или вставлять его в список точек образующих выпуклую

оболочку. Чтобы получить это оценку, мы на каждую точку должны тратить время

O(log N), то есть мы должна находить место вставки и вставлять точку

за O(log N). Такой алгоритм построил Препарата

[8].

В этом алгоритме необходимо быстро находить опорные прямые к выпуклому

многоугольнику P и проходящие через некоторую точку p. После

этого одну из цепей, на которые разбивают опорные точки границу выпуклого

многоугольника, заменить на p.

Будем называть опорную прямую pl левой, если многоугольник P

лежит справа от pl, и соответственно прямую pr правой, если

слева. Точки l и r будем называть опорными. Так же будем

различать вогнутые вершины, т.е. те для которых отрезок, соединяющий их

и p, пересекает внутренность многоугольника. А те, которые ни вогнутые

и ни опорные будут выпуклыми.

При поверке какой-то вершины на вогнутость или выгнутость мы можем определить,

где искать опорную точку. Тык же мы должны иметь возможность быстро удалить

цепочку вершин и вставить место нее p. Для этого нам нужно хранить

многоугольник не писком, как это делалось в предыдущих алгоритмах, а AWL или

другим сбалансированным деревом.

В этом дереве T переход к левому потомку будет соответствовать движению

по часовой стрелке по выпуклой оболочке, а для правого против часовой стрелки.

Для каждого узла в этом дереве мы должны иметь возможность получать доступ к

самой левому узлу. Если рассмотреть корневой узел дерева M и m

– самый левый узел, то они разбивают границу выпуклого многоугольника на две

цепи, причем одна хранится в левом поддереве M, а вторая в правом. В

зависимости от типа вершины М и m, а также от того, какой угол

(mpM) – левый или правый, можно определить в каком поддереве находится

опорная вершина.

Рассмотрим поиск левой опорной вершины. Если (mpM) – левый а m –

вогнутая или то (mpM) – правый а M – выпуклая, то поиск нежно

продолжать в левом поддереве, иначе – в правом. Аналогично и для правой опорной

вершины.

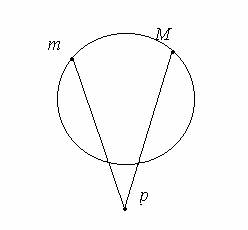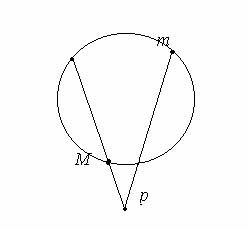
Рис. 4: Два варианта для m, M и p.

Таким способом мы находим за время O(log i) левую и правую

опорные прямые. После этого за время O(log i) мы можем удалить

все выпуклые вершины и сбалансируем дерево. Отсюда следует теорема:

Теорема 7. Выпуклая оболочка множества из N точек на плоскости может

быть найдена с помощью открытого алгоритма за время Q(N log N

) и со временем коррекции Q(log N).

Сравнительный анализ алгоритмов построения выпуклой оболочки

Так как теоретически показали, что время работы всех алгоритмов в среднем O

(log N), то следует ожидать при тестировании почти всегда результаты

отличающиеся на константу.

Проведем исследования зависимости времени работы алгоритмов от размеров

задачи при равномерном распределении точек:

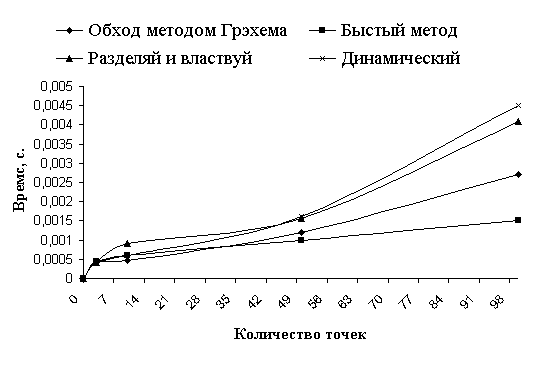
Рис. 5: Зависимость время выполнения алгоритмов при равномерном случайном

расположении точек (N<=100).

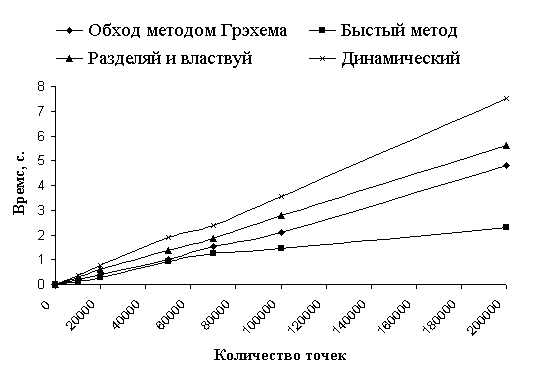
Рис. 6: Зависимость время выполнения алгоритмов при равномерном случайном

расположении точек (N<=200000).

Как видно из диаграмм, все алгоритмы в среднем при равномерном распределении

точек показали почти линейное время. Различается время примерно в одинаковое

число раз, что связано с реализацией данных алгоритмов. Так же видно, при

данном распределении быстрее всех работает быстрый алгоритм построения выпуклой

оболочки. Это объясняется тем, что в этом случае при каждом шаге он

отбрасывает примерно одинаковую часть точек. Поэтому на каждом i­­-том

уровне рекурсии происходит обработка Nki точек, где k

часть вершин, которая остается. Это k будет меньше единицы, и не будет

сильно изменяться на более глубоких вызовах рекурсивной процедуры. Отсюда

получаем то, что время будет стремиться к линейному.

Такого не должно наблюдаться при тестах, в которых почти все данные точки

будут являться вершинами выпуклой оболочки.

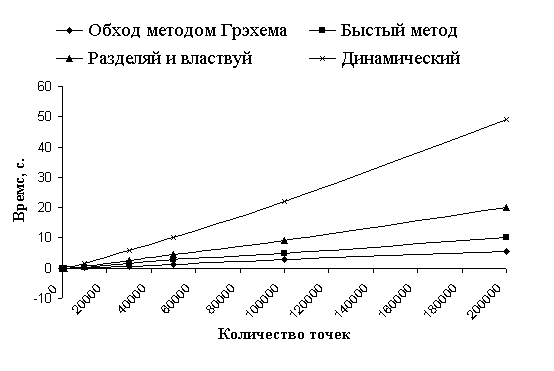
Рис. 7: Зависимость время выполнения при расположении точек на окружности.

Как видно в данном случае алгоритм Грэхема оказался самым эффективным. Быстрый

метод в этом случае не выбрасывает на каждом шаге точек, но так как делит их

примерно на равные части, то получается, что он работает примерно время O

(N log N), что вполне приемлемо. Что касается динамического

построения, то в процессе добавления точек в дерево попадают все вершины, а так

как при работе с AWL деревом в моей реализации используются сложные операции с

указателями то и процедура получилась медленной.

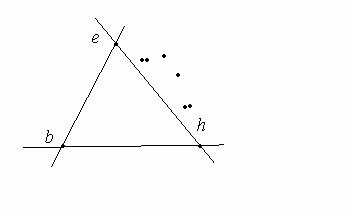
Рис. 8: Нежелательный случай расположения точек для быстрого алгоритма.

Из алгоритма быстрого построения следует, что в некоторых случая на каком-то

шаге может оказаться, что не была удалена ни одна вершина, и все точки

оказались по одну сторону от bh и eh (рис. 8). Если такое

случается очень редко, то это не отразится на времени выполнения значительно, а

если такое происходит на каждом шаге, то это приводит к оценке O(N

2). Для моей реализации этого алгоритма можно взять график ex

и точку, расположенную на оси ординат над точкой O.

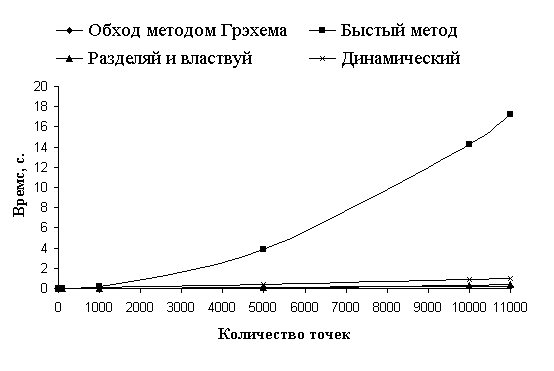
Рис. 9: Время работы быстрой оболочки O(N2).

Выводы

Как видно из результатов тестов, быстрый метод с данной задачей справляется

неудовлетворительно.

Теперь можно подвести итоги. В большинстве случаев самыми быстрыми являются

алгоритмы Грэхема и быстрый алгоритм. С учетом того, что они просты для

реализации, они вполне приемлемы для многих задач.

Но быстрый метод имеет существенный недостаток. Если нас интересует поведение

алгоритма в худшем случае, он неприемлем.

Алгоритм типа “разделяй и властвуй” не показал очень быстрых результатов и не

Страницы: 1, 2, 3, 4