|
принято называть коммутирующими.
Среди квадратных матриц выделим класс так называемых диагональных
матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны
нулю. Среди всех диагональных матриц с совпадающими элементами на главной
диагонали особо важную роль играют две матрицы. Первая из этих матриц
получается, когда все элементы главной диагонали равны единице, называется
единичной матрицей n-ого порядка и обозначается символом E
. Вторая матрица получается при всех элементах равных нулю и называется нулевой
матрицей n-ого порядка и обозначается символом O.
Допустим, что существует произвольная матрица A, тогда
AE = EA = A, AO = OA = O.
Первая из формул характеризует особую роль единичной матрицы Е,
аналогичную то роли, которую играет число 1 при перемножении
вещественных чисел. Что же касается особой роли нулевой матрицы О, то
ее выявляет не только вторая из формул, но и элементарно проверяемое равенство
: A + O = O + A = A. Понятие нулевой матрицы можно
вводить и не для квадратных матриц.
2. Определители. 2.1 Понятие определителя.
Прежде всего необходимо запомнить, что определители существуют только для
матриц квадратного вида, ибо для матриц другого типа не существует
определителей. В теории систем линейных уравнений и в некоторых других вопросах
удобно использовать понятие определителя, или детерминанта.
2.2 Вычисление определителей.
Рассмотрим какую-либо четверку чисел, записанных в виде матрицы 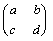
по два в строках и по два столбцах, Определителем или
детерминантом, составленным из чисел этой таблицы, называется число
ad—bc, обозначаемое так: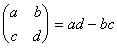
. Такой определитель Такой определитель
называется определителем второго порядка, поскольку для его составления
взята таблица из двух строк и двух столбцов. Числа, из которых составлен
определитель, называются его элементами; при этом говорят, что элементы
a и d составляют главную диагональ определителя,
а элементы b и c его побочную диагональ. Видно, что
определитель равен разности произведений пар элементов, стоящих на его главной
и побочной диагоналях . Определитель третьего и любого другого порядка
находится примерно также, а именно: Допустим, что у нас есть квадратная
матрица 
. Определителем следующей матрицы является такое выражение : a11a22a33 +
a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a22a31.. Как вы видите он
просчитывается довольно легко, если запомнить определенную последовательность.
С положительным знаком идут главная диагональ и образующиеся из элементов
треугольники, имеющие параллельную главной диагонали сторону, в данном случае
это треугольники a12a23a31, a13a21a32.
С отрицательным знаком идут побочная диагональ и треугольники ей
параллельные, т.е. a11a23a32 , a12a21a33. Таким образом находятся определители
любого порядка. Но бывают случаи, когда и этот метод становится довольно
сложным, например, когда элементов в матрице очень много, и для того, чтобы
сосчитать определитель нужно затратить уйму времени и внимания.
Существует более легкий способ вычисления определителя n-ого порядка, где n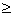
2. Договоримся называть минором любого элемента Aij матрицы n-ого порядка
определитель, соответствующий той матрице, которая получается из матрицы в
результате вычеркивания i-й строки и j-ого столбца ( той строки и того столбца,
на пересечении которых стоит элемент Aij ). Минор элемента Aij будем обозначать
символом 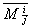 . В . В
этом обозначении верхний индекс обозначает номер строки, нижний – номер
столбца, ф черта над M означает, что указанные строка и
столбец вычеркиваются. Определителем порядка n,
соответствующим матрице, назовем число, равное 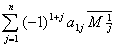
и обозначаемое символом 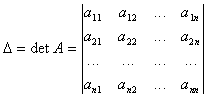
.
Теорема 1.1 Каков бы ни был номер строки i ( i =1, 2 ., n ),
для определителя n-ого порядка справедлива формула
 = det A = = det A = 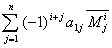
называемая разложением этого определителя по i-й строке
. Подчеркнем, что в этой формуле показатель степени, в которую возводится число
(-1), равен сумме номеров строки и столбца, на пересечении которых стоит
элемент Aij.
Теорема 1.2 Каков бы ни был номер столбца j ( j =1, 2 ., n ),
для определителя n-го порядка справедлива формула
 = det A = = det A = 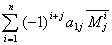
называемая разложением этого определителя по j-ому столбцу
.
2.3 Основные свойства определителей.
У определителей также есть свойства, с помощью которых задача их вычисления
становится более легкой. Итак, ниже устанавливается ряд свойств, которыми
обладает произвольный определитель n-го порядка.
1 . Свойство . Свойство
равноправности строк и столбцов. Транспонированием любой матрицы
или определителя называется операция, в результате которой меняются местами
строки и столбцы с сохранением порядка их следования. В результате
транспонирования матрицы A получается матрица, называется матрица, называемая
транспонированной по отношению к матрице A и обозначается
символом A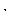
.
Первое свойство определителя формулируется так : при транспонировании
величина определителя сохраняется, т. е. 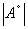
= 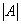 . .
2 . Свойство . Свойство
антисимметрии при перестановке двух строк ( или двух столбцов ). При
перестановке местами двух строк ( или двух столбцов ) определитель сохраняет
свою абсолютную величину, но меняет знак на противоположный. Для
определителя второго порядка это свойство проверяется элементарно ( из формулы
вычисления определителя второго порядка сразу вытекает, что определители
отличаются лишь знаком ).
3 . Линейное . Линейное
свойство определителя. Будем говорить, что некоторая строка (a) является
линейной комбинацией двух других строк ( b и c ) с коэффициентами 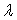
и 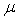 . Линейное . Линейное
свойство можно сформулировать так : если в определителе n-го порядка 
некоторая i-я строка является линейной комбинацией двух строк с коэффициентами 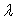
и 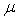 , то , то 
= 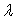 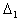
+ 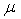 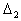
, где
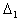 – определитель, у – определитель, у
которого i-я строка равна одной из двух строк линейной комбинации, а все
остальные строки те же, что и у 
, а 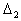 – –
определитель, у которого i-я строка равна второй из двух строк, а все остальные
строки те же, что и у 
.
Эти три свойства являются основными свойствами определителя, вскрывающими его
природу. Следующие пять свойств являются логическими следствиями трех
основных свойств.
Следствие 1. Определитель с двумя одинаковыми строками ( или
столбцами ) равен нулю.
Следствие 2. Умножение всех элементов некоторой строки ( или
некоторого столбца ) определителя на число a
равносильно умножению определителя на это число a. Иными
словами , общий множитель всех элементов некоторой строки ( или некоторого
столбца ) определителя можно вынести за знак этого определителя.
Следствие 3. Если все элементы некоторой строки ( или
некоторого столбца ) равны нулю, то и сам определитель равен нулю.
Следствие 4. Если элементы двух строк ( или двух столбцов )
определителя пропорциональны, то определитель равен нулю.
Следствие 5. Если к элементам некоторой строки ( или
некоторого столбца ) определителя прибавить соответствующие элементы другой
строки ( другого столбца ), умножение на произвольный множитель 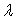
, то величина определителя не изменяется. Следствие 5, как и линейное свойство,
допускает более общую формулировку, которую я приведу для строк : если к
элементам некоторой строки определителя прибавить соответствующие элементы
строки, являющейся линейной комбинацией нескольких других строк этого
определителя ( с какими угодно коэффициентами ), то величена определителя не
изменится. Следствие 5 широко применяется при конкретном вычислении
определителей.
3. Системы линейных уравнений. 3.1 Основные определения.
...
3.2 Условие совместности систем линейных уравнений.
...
3.3 Решение систем линейных уравнений методом Крамера.
Известно, что используя матрицы мы можем решать различные системы уравнений,
при чем эти системы могут быть какой угодно величены и иметь сколько угодно
переменных. С помощью нескольких выводов и формул решение огромных систем
уравнений становится довольно быстрым и более легким.
В частности, я опишу методы Крамера и Гаусса. Наилегчайшим способом является
метод Крамера ( для меня ), или как его еще называют – формула Крамера. Итак,
допустим, что мы имеем какую-либо систему уравнений
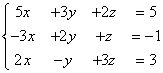 , в виде , в виде
матрицы эту систему можно записать таким образом : A = 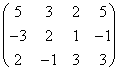
, где ответы будут уравнений будут находится в последнем столбце. Теперь мы
введем понятие основного определителя; в данном случае он будет выглядеть
таким образом :
 = = 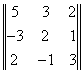
. Основным определителем как вы уже заметили является матрица составленная из
коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е.
в первом столбце стоят коэффициенты, которые находятся при x
, во втором столбце при y, и так далее. Это очень важно,
ибо в следующих действиях мы будем заменять каждый столбец коэффициентов при
переменной на столбец ответов уравнений. Итак, как я уже говорил, мы заменяем
столбец при первой переменной на столбец ответов, затем при второй, конечно это
все зависит от того, сколько переменных нам нужно найти.
 1 = 1 = 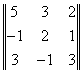 , ,  2 = 2 = 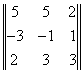 , ,  3 = 3 = 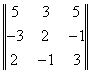 . .
Затем нужно найти определители 
1 ,  2 , 2 , 
3 . Как находится определитель третьего порядка вы уже знаете. А вот здесь мы и
применяем правило Крамера. Оно выглядит так :
x1 = 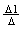 , x2 = , x2 = 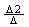
, x3 = 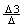 – –
для данного случая, а в общем виде оно выглядит следующим образом :
xi = 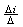 . .
Определитель составленный из коэффициентов при неизвестных, называется
определителем системы.
3.4 Решение систем линейных уравнений методом Гаусса.
...
4. Обратная матрица. 4.1 Понятие обратной матрицы.
..
4.2 Вычисление обратной матрицы.
..
Список литературы.
1. В. А. Ильин, Э. Г. Позняк “Линейная Алгебра”
2. Г. Д. Ким, Е. В. Шикин “Элементарные преобразования в линейной алгебре”
Страницы: 1, 2
| 


