| Реферат: Комплексные числа |
Запись комплексного числа Z в виде A+B·i называется
алгебраической формой комплексного числа. Помимо алгебраической формы
используются и другие формы записи комплексных чисел.
Рассмотрим тригонометрическую форму записи комплексного числа.
Действительная и мнимая части комплексного числа Z=A+B·i
выражаются через его модуль 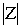 = r и аргумент j следующим образом:
A= r·cosj ; B= r·sinj.
Число Z можно записать так:
Z= r·cosj+ i·
= r и аргумент j следующим образом:
A= r·cosj ; B= r·sinj.
Число Z можно записать так:
Z= r·cosj+ i·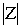 ·sinj = r·(cosj + i·sinj)
Z = r·(cosj + i·sinj) (2)
Эта запись называется тригонометрической формой комплексного числа.
r = ·sinj = r·(cosj + i·sinj)
Z = r·(cosj + i·sinj) (2)
Эта запись называется тригонометрической формой комплексного числа.
r =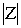 – модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z – модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z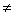 0 называется величина угла между положительным направлением действительной оси и
вектором Z, причем величина угла считается положительной, если отсчет ведется
против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается
только своим модулем.
Как уже говорилось выше
0 называется величина угла между положительным направлением действительной оси и
вектором Z, причем величина угла считается положительной, если отсчет ведется
против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается
только своим модулем.
Как уже говорилось выше 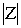 = r = = r =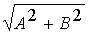 , равенство (2) можно записать в виде
A+B·i= , равенство (2) можно записать в виде
A+B·i=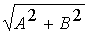 ·
cosj + i· ·
cosj + i·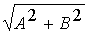 ·
sinj, откуда приравнивая действительные и мнимые части, получим:
cosj = ·
sinj, откуда приравнивая действительные и мнимые части, получим:
cosj =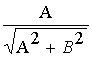 , sinj = , sinj =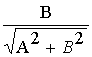 (3)
Если sinj поделить на cosj получим:
tgj= (3)
Если sinj поделить на cosj получим:
tgj=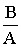 (4)
Эту формулу удобней использовать для нахождения аргумента j, чем формулы
(3). Однако не все значения j, удовлетворяющие равенству (4), являются
аргументами числа A+B·i . Поэтому при нахождении аргумента нужно
учесть, в какой четверти расположена точка A+B·i.
7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА
КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формы удобно находить произведение и частное
комплексных чисел.
Пусть Z1= r1·(cosj1 + i·sinj1), Z2 = r2·(cosj2 + i·sinj2). Тогда:
Z1Z2= r1·r2[cosj1·cosj2 – sinj1·sinj2 + i·( sinj1·cosj2 + cosj1·sinj2)]=
= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)].
Таким образом, произведение комплексных чисел, записанных в
тригонометрической форме, можно находить по формуле:
Z1Z2= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)] (5)
Из формулы (5) следует, что при умножении комплексных чисел их модули
перемножаются, а аргументы складываются.
Если Z1=Z2 то получим:
Z2=[r·(cosj + i·sinj)]2= r2·(cos2j + i·sin2j)
Z3=Z2·Z= r2·(cos2j + i·sin2j)·r·(cosj + i·sinj)=
= r3·(cos3j + i·sin3j)
Вообще для любого комплексного числа Z= r·( cosj + i·sinj) (4)
Эту формулу удобней использовать для нахождения аргумента j, чем формулы
(3). Однако не все значения j, удовлетворяющие равенству (4), являются
аргументами числа A+B·i . Поэтому при нахождении аргумента нужно
учесть, в какой четверти расположена точка A+B·i.
7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА
КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формы удобно находить произведение и частное
комплексных чисел.
Пусть Z1= r1·(cosj1 + i·sinj1), Z2 = r2·(cosj2 + i·sinj2). Тогда:
Z1Z2= r1·r2[cosj1·cosj2 – sinj1·sinj2 + i·( sinj1·cosj2 + cosj1·sinj2)]=
= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)].
Таким образом, произведение комплексных чисел, записанных в
тригонометрической форме, можно находить по формуле:
Z1Z2= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)] (5)
Из формулы (5) следует, что при умножении комплексных чисел их модули
перемножаются, а аргументы складываются.
Если Z1=Z2 то получим:
Z2=[r·(cosj + i·sinj)]2= r2·(cos2j + i·sin2j)
Z3=Z2·Z= r2·(cos2j + i·sin2j)·r·(cosj + i·sinj)=
= r3·(cos3j + i·sin3j)
Вообще для любого комплексного числа Z= r·( cosj + i·sinj)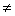 0 и любого натурального числа n справедлива формула:
Zn =[ r·(cosj + i·sinj)]n= rn·( cosnj+ i·sinnj), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел, записанных в тригонометрической форме, можно
находить по формуле:
0 и любого натурального числа n справедлива формула:
Zn =[ r·(cosj + i·sinj)]n= rn·( cosnj+ i·sinnj), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел, записанных в тригонометрической форме, можно
находить по формуле:
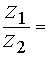 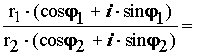 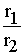 [ cos(j1 – j2) + i·sin(j1 – j2)]. (7) [ cos(j1 – j2) + i·sin(j1 – j2)]. (7)
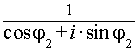 = = 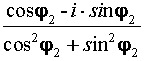 = cos(–j2) + i·sin(–j2)
Используя формулу 5 = cos(–j2) + i·sin(–j2)
Используя формулу 5
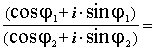 (cosj1 + i·sinj1)×( cos(–j2) + i·sin(–j2)) =
cos(j1 – j2) + i·sin(j1 – j2).
Пример 3:
Z3 = –8
Число –8 запишем в тригонометрической форме
8 = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:
r3×(cos3j + i×sin3j) = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Тогда 3j =p + 2pk, kÎZ
j = (cosj1 + i·sinj1)×( cos(–j2) + i·sin(–j2)) =
cos(j1 – j2) + i·sin(j1 – j2).
Пример 3:
Z3 = –8
Число –8 запишем в тригонометрической форме
8 = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:
r3×(cos3j + i×sin3j) = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Тогда 3j =p + 2pk, kÎZ
j = 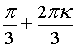 , kÎZ
r3 = 8
r = 2
Следовательно:
Z = 2·( cos( , kÎZ
r3 = 8
r = 2
Следовательно:
Z = 2·( cos(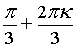 ) + i·sin( ) + i·sin(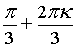 )), kÎZ
k = 0,1,2...
k = 0
Z1 = 2·( cos )), kÎZ
k = 0,1,2...
k = 0
Z1 = 2·( cos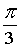 + i·sin + i·sin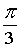 ) = 2·( ) = 2·(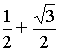 i) = 1+ i) = 1+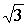 ×i
k = 1
Z2 = 2·( cos( ×i
k = 1
Z2 = 2·( cos(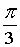 + + 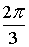 ) + i·sin( ) + i·sin(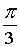 + + 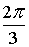 )) = 2·( cosp + i·sinp) = –2
k = 2
Z3 = 2·( cos( )) = 2·( cosp + i·sinp) = –2
k = 2
Z3 = 2·( cos(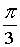 + + 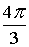 ) + i·sin( ) + i·sin(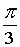 + + 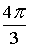 )) = 2·( cos )) = 2·( cos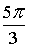 + i·sin + i·sin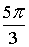 ) = 1– ) = 1–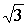 ×i
Ответ: Z13 = ×i
Ответ: Z13 = 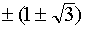 ; Z2 = –2
Пример 4:
Z4 = 1
Число 1 запишем в тригонометрической форме
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:
r4×(cos4j + i×sin4j) = cos(2pk) + i·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j = ; Z2 = –2
Пример 4:
Z4 = 1
Число 1 запишем в тригонометрической форме
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:
r4×(cos4j + i×sin4j) = cos(2pk) + i·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j = 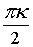 , kÎZ
r4 = 1
r = 1
Z = cos , kÎZ
r4 = 1
r = 1
Z = cos 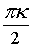 + i×sin + i×sin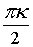 k = 0,1,2,3...
k = 0
Z1 = cos0+ i×sin0 = 1 + 0 = 1
k = 1
Z2 = cos
k = 0,1,2,3...
k = 0
Z1 = cos0+ i×sin0 = 1 + 0 = 1
k = 1
Z2 = cos 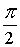 + i×sin + i×sin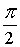 = 0 + i = i
k = 2
Z3 = cosp + i·sinp = –1 + 0 = –1
k = 3
Z4 = cos = 0 + i = i
k = 2
Z3 = cosp + i·sinp = –1 + 0 = –1
k = 3
Z4 = cos 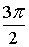 + i×sin + i×sin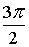 Ответ: Z13 =
Ответ: Z13 = 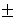 1
Z24 = 1
Z24 = 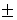 i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Из формулы 6 видно, что возведение комплексного числа r·( cosj + i
·sinj) в целую положительную степень с натуральным показателем его модуль
возводится в степень с тем же показателем, а аргумент умножается на показатель
степени.
[ r·(cosj + i·sinj)]n= rn·( cos nj + i·sin nj)
Число Z называется корнем степени n из числа w ( обозначается i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Из формулы 6 видно, что возведение комплексного числа r·( cosj + i
·sinj) в целую положительную степень с натуральным показателем его модуль
возводится в степень с тем же показателем, а аргумент умножается на показатель
степени.
[ r·(cosj + i·sinj)]n= rn·( cos nj + i·sin nj)
Число Z называется корнем степени n из числа w ( обозначается 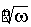 ), если Zn =w.
Из данного определения вытекает, что каждое решение уравнения Zn
= w является корнем степени n из числа w. Другими словами, для того,
чтобы извлечь корень степени n из числа w, достаточно решить уравнение
Zn = w. Если w=0, то при любом n уравнение Zn =
w имеет только одно решение Z= 0. Если w ), если Zn =w.
Из данного определения вытекает, что каждое решение уравнения Zn
= w является корнем степени n из числа w. Другими словами, для того,
чтобы извлечь корень степени n из числа w, достаточно решить уравнение
Zn = w. Если w=0, то при любом n уравнение Zn =
w имеет только одно решение Z= 0. Если w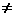 0, то и Z
0, то и Z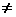 0
, а, следовательно, и Z и w можно представить в тригонометрической форме
Z = r·(cosj + i·sinj), w = p·(cosy + i·siny)
Уравнение Zn = w примет вид:
rn·( cos nj + i·sin nj) = p·( cosy + i·siny)
Два комплексных числа равны тогда и только тогда, когда равны их модули, а
аргументы отличаются слагаемыми, кратными 2p. Следовательно, rn = p
и nj = y + 2pk, где kÎZ или r = 0
, а, следовательно, и Z и w можно представить в тригонометрической форме
Z = r·(cosj + i·sinj), w = p·(cosy + i·siny)
Уравнение Zn = w примет вид:
rn·( cos nj + i·sin nj) = p·( cosy + i·siny)
Два комплексных числа равны тогда и только тогда, когда равны их модули, а
аргументы отличаются слагаемыми, кратными 2p. Следовательно, rn = p
и nj = y + 2pk, где kÎZ или r = 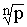 и j =
и j = 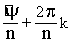 , где
kÎZ.
Итак, все решения могут быть записаны следующим образом:
ZK= , где
kÎZ.
Итак, все решения могут быть записаны следующим образом:
ZK=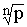 [cos( [cos(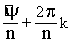 ) + i·sin( ) + i·sin(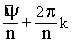 )], kÎZ (8)
Формулу 8 называют второй формулой Муавра.
Таким образом, если w )], kÎZ (8)
Формулу 8 называют второй формулой Муавра.
Таким образом, если w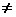 0, то существует ровно n корней степени n из числа w: все они содержатся в
формуле 8. Все корни степени n из числа w имеют один и тот же модуль
0, то существует ровно n корней степени n из числа w: все они содержатся в
формуле 8. Все корни степени n из числа w имеют один и тот же модуль 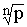 , но разные аргументы, отличающиеся слагаемым, кратным числу
, но разные аргументы, отличающиеся слагаемым, кратным числу 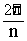 . Отсюда следует, что комплексные числа, являющиеся корнями степени n из
комплексного числа w, соответствует точкам комплексной плоскости, расположенным
в вершинах правильного n – угольника, вписанного в окружность
радиуса
. Отсюда следует, что комплексные числа, являющиеся корнями степени n из
комплексного числа w, соответствует точкам комплексной плоскости, расположенным
в вершинах правильного n – угольника, вписанного в окружность
радиуса 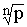 с центром
в точке Z = 0.
Символ с центром
в точке Z = 0.
Символ 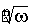 не имеет
однозначного смысла. Поэтому, употребляя его, следует четко представлять себе,
что под этим символом подразумевается. Например, используя запись не имеет
однозначного смысла. Поэтому, употребляя его, следует четко представлять себе,
что под этим символом подразумевается. Например, используя запись 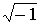 , следует подумать о том, чтобы было ясно, понимается под этим символом пара
комплексных чисел i и –i, или одно, то какое
именно.
Уравнения высших степеней
Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо
сложнее обстоит дело в случае общего алгебраического уравнения степени n:
an×Zn + an–1×Zn–1 +...+ a1×Z1 + a0 = 0 (9)
Где an,..., a0 – заданные комплексные числа.
В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое
уравнение имеет в множестве комплексных чисел по крайней мере один корень.
Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.
Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9
всегда может быть представлена в виде произведения:
, следует подумать о том, чтобы было ясно, понимается под этим символом пара
комплексных чисел i и –i, или одно, то какое
именно.
Уравнения высших степеней
Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо
сложнее обстоит дело в случае общего алгебраического уравнения степени n:
an×Zn + an–1×Zn–1 +...+ a1×Z1 + a0 = 0 (9)
Где an,..., a0 – заданные комплексные числа.
В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое
уравнение имеет в множестве комплексных чисел по крайней мере один корень.
Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.
Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9
всегда может быть представлена в виде произведения:
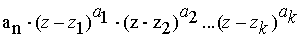 ,
Где Z1, Z2,..., ZK – некоторые различные комплексные числа,
а a1,a2,...,ak – натуральные числа, причем:
a1 + a2 + ... + ak = n
Отсюда следует, что числа Z1, Z2,..., ZK
являются корнями уравнения 9. При этом говорят, что Z1
является корнем кратности a1, Z2 – корнем
кратности a2 и так далее.
Если условиться считать корень уравнения столько раз, какова его кратность,
то можно сформулировать теорему: каждое алгебраическое уравнение степени n
имеет в множестве комплексных чисел ровно n корней.
Теорема Гаусса и только что сформулированная теорема дают решения о
существовании корней, но ничего не говорят о том, как найти эти корни. Если
корни первой и второй степени могут быть легко найдены, то для уравнений
третей и четвертой степеней формулы громоздки, а для уравнений степени выше
четвертой таких формул вообще не существует. Отсутствие общего метода не
мешает отыскивать все корни уравнения. Для решения уравнения с целыми
коэффициентами часто оказывается полезной следующая теорема: целые корни
любого алгебраического уравнения с целыми коэффициентами являются делителями
свободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an×Zn + an–1×Zn–1 +...+ a1×Z1 + a0 = 0
с целыми коэффициентами. Тогда
an×kn + an–1×kn–1 +...+ a1×k1 + a0 = 0
a0 = – k(an×kn–1 + an–1×kn–2 +...+ a1)
Число в скобках, при сделанных предположениях, очевидно, целое, значит k –
делитель числа a0.
9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число,
Z – неизвестное.
Это уравнение:
1. имеет один корень, если a = 0.
2. имеет два действительных корня Z1,2= ,
Где Z1, Z2,..., ZK – некоторые различные комплексные числа,
а a1,a2,...,ak – натуральные числа, причем:
a1 + a2 + ... + ak = n
Отсюда следует, что числа Z1, Z2,..., ZK
являются корнями уравнения 9. При этом говорят, что Z1
является корнем кратности a1, Z2 – корнем
кратности a2 и так далее.
Если условиться считать корень уравнения столько раз, какова его кратность,
то можно сформулировать теорему: каждое алгебраическое уравнение степени n
имеет в множестве комплексных чисел ровно n корней.
Теорема Гаусса и только что сформулированная теорема дают решения о
существовании корней, но ничего не говорят о том, как найти эти корни. Если
корни первой и второй степени могут быть легко найдены, то для уравнений
третей и четвертой степеней формулы громоздки, а для уравнений степени выше
четвертой таких формул вообще не существует. Отсутствие общего метода не
мешает отыскивать все корни уравнения. Для решения уравнения с целыми
коэффициентами часто оказывается полезной следующая теорема: целые корни
любого алгебраического уравнения с целыми коэффициентами являются делителями
свободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an×Zn + an–1×Zn–1 +...+ a1×Z1 + a0 = 0
с целыми коэффициентами. Тогда
an×kn + an–1×kn–1 +...+ a1×k1 + a0 = 0
a0 = – k(an×kn–1 + an–1×kn–2 +...+ a1)
Число в скобках, при сделанных предположениях, очевидно, целое, значит k –
делитель числа a0.
9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число,
Z – неизвестное.
Это уравнение:
1. имеет один корень, если a = 0.
2. имеет два действительных корня Z1,2=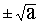 , если a > 0.
3. не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2
× , если a > 0.
3. не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2
× = i
2×( = i
2×(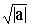 )
2. Тогда уравнение Z2 = a запишется в виде:
Z2 – i2×( )
2. Тогда уравнение Z2 = a запишется в виде:
Z2 – i2×(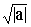 )2 = 0
т.е. (Z – i×
)2 = 0
т.е. (Z – i×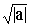 )(Z + i× )(Z + i×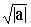 ) = 0
Следовательно, уравнение имеет два корня: Z1,2 = ) = 0
Следовательно, уравнение имеет два корня: Z1,2 = 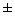 i× i×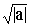 Введенное понятие корня из отрицательного числа позволяет записать корни
любого квадратного уравнения с действительными коэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2=
Введенное понятие корня из отрицательного числа позволяет записать корни
любого квадратного уравнения с действительными коэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2=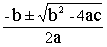 (10)
Итак, при любых действительных a(a (10)
Итак, при любых действительных a(a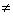 0), b, c корни уравнения можно находить по формуле 10. При это если
дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен , то уравнение a×Z2 + b×Z + c = 0 два
действительных различных корня. Если D = 0, то уравнение a×Z2
+ b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z
2 + b×Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и
известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2
+ b×Z + c = 0, a
0), b, c корни уравнения можно находить по формуле 10. При это если
дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен , то уравнение a×Z2 + b×Z + c = 0 два
действительных различных корня. Если D = 0, то уравнение a×Z2
+ b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z
2 + b×Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и
известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2
+ b×Z + c = 0, a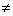 0. Тогда справедливы свойства:
1. Теорема Виета: Z1 + Z2 = –
0. Тогда справедливы свойства:
1. Теорема Виета: Z1 + Z2 = –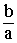 Z1×Z2 =
Z1×Z2 = 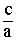 2. При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 =
2. При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 = 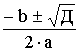 Z1,2 =
Z1,2 =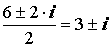 Ответ: Z1 = Z2 = 3 + i
Пример 6:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 =
Ответ: Z1 = Z2 = 3 + i
Пример 6:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = 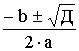 = = 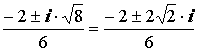 Z1,2 =
Z1,2 =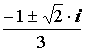 Z1 = – (
Z1 = – (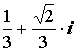 )
Z2 = – )
Z2 = –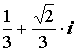 Ответ: Z1 = Z2 = –
Ответ: Z1 = Z2 = –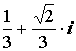 Пример 7:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 =
Пример 7:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = 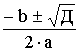 = = 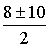 = 4 = 4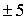 t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 =
t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 =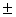 3 Z = 3 Z = 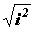 Z3,4 =
Z3,4 =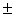 i
Ответ: Z1,2 = i
Ответ: Z1,2 =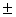 3, Z3,4 = 3, Z3,4 =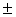 i
Пример 8:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = i
Пример 8:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = 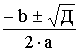 = = 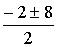 = –1 = –1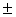 4
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 = 4
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 =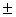 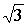 Z2 = i2·5
Z1,2 =
Z2 = i2·5
Z1,2 =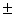 i i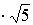 Ответ: Z1,2 =
Ответ: Z1,2 = i i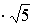 , Z3,4 = , Z3,4 =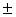 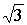 Пример 9:
Z2 = 24 – 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i –Y2
X2 + 2·X·Y·i – Y2 = 24 – 10·i
(X2 – Y2) + 2·X·Y·i = 24 – 10·i
Пример 9:
Z2 = 24 – 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i –Y2
X2 + 2·X·Y·i – Y2 = 24 – 10·i
(X2 – Y2) + 2·X·Y·i = 24 – 10·i
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



