|
, и 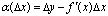
Поскольку 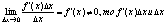 - б.м. одного порядка малости. - б.м. одного порядка малости.
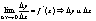 - б.м. одного порядка малости - б.м. одного порядка малости 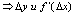 - б.м. эквивылентные, т.е. - б.м. эквивылентные, т.е. 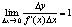
Пусть 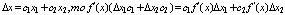
**************
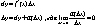
Zm1: 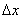 и х – независимые переменные, т.е. и х – независимые переменные, т.е. 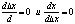
Zm1: 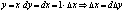 для независимых переменных. для независимых переменных.
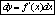
37.Правила диференц суммы,разн,произв,частн
1) 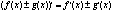 ; ;
2) 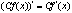 , где , где 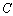 - постоянная; - постоянная;
3) 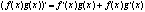 ; ;
4) 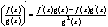 ; ;
5) если 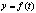 , а , а 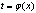 , то производная сложной функции , то производная сложной функции 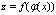 находится по формуле находится по формуле
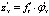 , ,
где индексы указывают, по какому аргументу производится дифференцирование.
38.Вычислен производных элемент.ф-ий: x^n,nЄN,cos,sin,tg ,ctg,
loga(основание)Х(а>0,a≠1,x>0)
39.Th о произв сложной ф-ии
Пусть:
1. 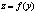 - дифф. в точке y0 . - дифф. в точке y0 .
2. 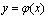 - дифф. в точке х0 . - дифф. в точке х0 .
3. 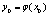
тогда сложная ф-ия 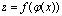 - дифф. в точке х0 и справедлива формула: - дифф. в точке х0 и справедлива формула:

Доказательство:
1. 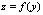 - дифф. в точке y0 - дифф. в точке y0 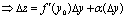
2. 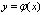 - дифф. в точке х0 - дифф. в точке х0 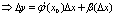
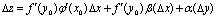
3. 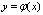 - дифф. в точке х0 а значит непрерывна в этой точке - дифф. в точке х0 а значит непрерывна в этой точке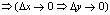 . .
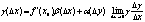
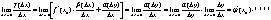
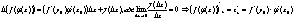
40.Производная ф-ий x^α, αЄR(прием логарифм. Диф)
41.Th о производной обратной ф-ии
Предложение: Если производная обратной функции g для ф-ции f существует в
точке y0, то g’(y0)=1/f’(x0), где y0
=f(x0)
Доказательство: g(f(x))=x g’(f(x))=1
g’(f(x0))=g’(f(x0))*f’(x0)=1, g’(f(x0))=g(y0)=1/f’(x0)
Теорема: Пусть ф-ция f строго монотонно и непрерывно отображает (a,b) в
(а,b) тогда $ обратная ей ф-ция g, которая строго монотонно и непрерывно
отображает (а,b) в (a,b). Если f диф-ма в точке x0Î(a,b) и
f’(x0)¹0, то g диф-ма в точке y0=f(x0) и
g’(y0)=1/f’(x0)
Доказательство:
Возьмем произвольную последовательность сходящуюся к y0: yN
®y0, yN¹y0 => $ посл-ть xN:
xN=g(yN), f(xN)=yN
g(yN)-g(y0)/yN-yO = xN-x
O/f(yN)-f(yO) = 1/f(yN)-f(yO
)/xN-xO ® 1/f’(xo) при n®¥, получили при xN
®xO g(yN)-g(yO)/yN-yO
®1/f’(xO) => g’(уO)=1/f’(xO)
42.Произв ф-ии: arcsinx,arccosx,arctgx,acctgx,a^x(a>0,a≠1)
1) x®Arcsin x по теореме имеем Arcsin’x=1/Sin’y, где Sin y=x при условии, что
Sin’y<0, получаем (используя производную синуса): Arcsin’x=1/Cos y, т.к.
Arcsin: [-1,1]®[-П/2,П/2] и Cos:[-П/2,П/2]®[0,1], то Cos y³0 и, значит
Arcsin’x = 1/Cos y = 1/(1-Sin2y)1/2 = 1/(1-x2)
1/2
2) x®Arccos’x = -1/(1-x2)1/2
3) x®Arctg’x = 1/1+x2
4) x®Arcctg’x= -1/1+x2
5) y=a^x(в степени х) y ‘ =a^xlna Док-во:y=a^x является обратной для ф-ии
x=loga(a-основание)y. Т.к. x’(y)=(1/y)loga(a-осн)e, то из соотношения loga(a-
OCH)b=1/logb(b-OCH)a получим y’(x)=1/x’(y)=y/loga(a-OCH)e=a^x(в степени х)lna
43.Производная высших порядков
Определение: Если ф-ция f диф-ма в некоторой окрестности точки xO
, то ф-ция f’(x):x®f’(x) в свою очередь может оказаться диф-мой в точке xO
или даже в некоторой ее окрестности. Производная ф-ции f’(x) - называется
второй производной (или производной порядка 2) ф-ции f в точке xO и
обознача ется f”(x). Аналогично определяется третья и четвертая производная и
так далее. Для единообразия обозначаем через fN(xO) -
производную порядка n функции f в точке xO и при n=0 считаем f0
(xO)=f(xO).
Замечание: Cуществование производной порядка n требует того чтобы
существовала производная пордка (n-1) уже в некоторой окрестности точки xO
(следует из теоремы о связи диф-ти и непрерывности), в таком случае функция x®f
N-1(x) непрерывна в точке xO, а при n³2 все производные
порядка не выше (n-2) непрерывны в некоторой окрестности точки xO.
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную
функцию у=f(g(t)). Если существуют производные у’(х) и х’(t) то cуществует
производная у’(t)=у’(х)*х’(t).
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную
функцию у=f(g(t)) Если существуют производные у’(х) и х’(t) то существует
производная у’(t)=у’(х)*х’(t)
+нужно док-во
44.Диференциалы высших порядков
dy= f‘(x)dx – диф. первого порядка ф-ции f(x) и обозначается d^2y, т.е.
d^2y=f‘‘(x)(dx)^2. Диф. d(d^(n-1)y) от диф. d^(n-1)y наз-ся диф. n-ного
порядка ф-ции f(x) и обознач. d^ny.
Опр-ие: Дифференциалом n-го порядка функции у=f(х) называется
дифференциал первого порядка от дифференциала (n-1)-го порядка. (обозначается
dny)По определению dny= d(dn-1
y). Иногда dy называют диф. Первого порядка. В общем случае, dn
y=f(n)(х)dxn, в предположении,
что n-ая производная f(n)(х) сущ-ет.
+нужно док-во
45.Возрастание и убывание ф-ии в точке. Достаточное условие возрастан и
убыван ф-ии в точке
46.Понятие локального экстремума, необходимое условие локального экстремума
Опр-ие: Функция у=f(х) имеет в точке x0 локальный
максимум, если сущ-ет окрестность (х0-d, х0+d),
для всех точек х которой выполняется неравенство f(х)£f(х0
). Аналогично определяется локальный минимум, но выполняться должно
равенство f(х)³f(х0).
Теорема Ферма: Если функция у=f(х) имеет в точке х0 локальный
экстремум и дифференцируема в этой точке, то ее производная f'(х0
) равна нулю.
Док-во: Проведем его для случая максимума в точке х0. Пусть
(х0-d, х0+d) - та окрестность, для точек которой
выполняется неравенство
Здесь возможно как 1 и 2 варианты, но | ∆х| <δ
При ∆х>0, будет ∆y:∆x ≤0, поэтому
При ∆х<0, будет ∆y:∆x ≥0, поэтому
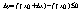
По условию теоремы, существует производная f'(х0)А это
означает, что правая производная fпр'(х0) и левая
производная fл'(х0) равны между собой: f
пр'(х0)= fл'(х0)= f'(х0).
Таким образом, с одной стороны, f'(х0)≤0, с другой
стороны, f'(х0)≥0, что возможно лишь, когда f'(х
0)=0.
47.Th Роля
Пусть ф-ция f(x) удовл. сл. усл.
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) принимает на коцах отрезков равные значения f(a)=f(b), тогда на (a,b) $ т-
ка такая что f‘(c)=0, т.е. с-крит. т-ка.
Док-во. Р-рим сначала, тривиальный случай, f(x) постоянная на
[a,b] (f(a)=f(b)), тогда f‘(x)=0 $ x Î (a,b), любую т-ку можно взять в
кач-ве с. Пусть f¹ const на [a,b], т.к. она непрер. на этом отрезке, то по
т-ме Вейерштрасса она достигает своего экстрем. на этом отрезке и max и min.
Поскольку f принимает равные знач. в гранич. т-ках, то хотя бы 1- экстр. – max
или min обязательно достигается во внутр. т-ке. сÎ(a,b) (в противном
случае f=const), то по т-ме Ферма, тогда f‘(c)=0, что и требовалось д-ть.
48.Th Логранжа (формула конечн.приращен)
Пусть ф-ция f(x) непрер. на отрезке [a,b] и диф. на интервале (a,b), тогда " т.
х и x+Dx Î [a,b] $ т-ка С лежащая между х и х+Dх такая что спаведлива
ф-ла (f(x+Dx)-f(x))=f(c)*Dx (7) => при сравнении с ф-лой приращения ф-ций с
диф. заметим, что (7) явл. точной ф-лой, однако теперь пр-ная фолжна считаться
в некоторой средней т-ке С «алгоритм» выбора которой неизвестен. Крайнее
значение (a,b) не запрещены.
Придадим ф-ле (7) классический вид => x=a x+Dx=b+> тогда ф-ла
(7)=(f(b)-f(a))/(b-a)=f‘(c) (7‘) – ф-ла конечных приращений Логранджа.
(f(b)-f(a))/(b-a)=f‘(c) (1)
Док-во сводится к сведению к т-ме Ролля. Р-рим вспом. ф-цию
g(x)=f(x)-f(a)-(f(b)-f(a))/(b-a) * (x-a)
Пусть ф-ция g(x) удовл. всем усл. т-мы Ролля на [a,b]
А)Непрерывна на [a,b]
Б) Дифференц. на (a,b)
В) g(a)=g(b)=0
Все усл. Ролля соблюдены, поэтому $ т-ка С на (a,b) g‘(c)=0 g‘(c)=f‘(x)-
(f(b)-f(a))/(b-a). Ф-ла (1) наз-ся ф-лой конечных приращений.
49.Th Коши(обобщенная формула конечн.приращен)
Теорема Коши: Пусть функции у=f(х) и у=g(х) неперырвны на отрезке
[a,b],дифференцируемы хотя бы в открытом промежутке (a,b) и на этом промежутке
g'(х) не обращается в нуль. Тогда существует такая точка c Î
(a,b), что выполняется равенство (1)
Докозательство: Вначале отметим, что знаменатель g(b)-g(a) ≠ 0
,т.к. из равенства g(b)=g(a) следовало бы по теореме Ролля, что
производная g'(х) обратилась бы в нуль в какой-нибудь точке промежутка
(a,b), что противоречит условию g'(х)≠0. Образуем вспомогательную
функцию:
К ней применима теорема Ролля: F(х) непрерывна в [a,b] и дифференцируема в
(a,b) как сумма функций, непрерывных и дифференцируемых в соответствующих
промежутках, кроме того, как легко проверить непосредственно, F(a)=F(b)=0.
Следовательно, существует точка c Î (a,b), , такая, что F'(c)=0.
Вычисляем:
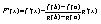
Подставляем x=c:
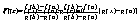
После деления на g'(х) (причем как говорилось раньше g'(х) ¹0), мы
приходим к формуле (1)
50.Усл. монотонности ф-ии по интервалам(монотонной,строгомонот ф-ии)
51.Правило Лопиталя (без док-ва,примеры)
Раскрытие 0/0. 1-е правило Лопиталя. Если lim(x®a)f(x)=
lim(x®a)g(x), то lim(x®a)f(x)/g(x)= lim(x®a)f‘(x)/g‘(x), когда предел $
конечный или бесконечный.
Раскрытие ¥/¥. Второе правило.
Если lim(x®a)f(x)= lim(x®a)g(x)=¥, то lim(x®a)f(x)/g(x)=
lim(x®a)f‘(x)/g‘(x). Правила верны тогда, когда
x®¥,x®-¥,x®+¥,x®a-,x®a+.
Неопред-ти вида 0¥, ¥-¥, 0^0, 1^¥, ¥^0.
Неопр. 0¥, ¥-¥ сводятся к 0/0 и ¥/¥ путем алгебраических
преобразований. А неопр. 0^0, 1^¥, ¥^0 с помощью тождества
f(x)^g(x)=e^g(x)lnf(x) сводятся к неопр вида 0
52.Стационарные точки (достаточн.усл.экстремума)
53.Экстремум ф-ии, недиф. В данной точке.
Th пусть ф-ия f(x) дифференцируема всюду в некоторой окрестности точки с за
исключением,может быть,самой точки с.Тогда, если в пределах указанной
окрестности f’(x)>0 слева от точки с и f’(x)<0 справа от точки с,то
функция f(x) имеет в точке с локальный максимум.Если f’(x)<0 слева от точки
с и f’(x)>0 справа от точки с, то ф-ия имеет в точке с локальный минимум.
Если ф-ия имеет один и тот же знак слева и справа от точки с, то экстремума в
точке с нет.
(док-во такое же как в вопросе «Стационарные точки, первое достаточное
условие локального экстремума)
54.Два достаточных условия экстремума.
55.Направление выпуклости ф-ии (опр,признаки)
Опр. Ф-ция явл. выпуклой (вогнутой) на (a,b) если кассат. к граф-ку ф-ции в
любой т-ке интервала, лежит ниже (выше) гр. ф-ции.
y=y0+f‘(x0)(x-x0)=f(x0)+f‘(x0)(x-x0) – линейная ф-ция х, который не
превосходит f(x) и не меньше f(x) в случае вогнутости неравенства хар-щие
выпуклость (вогнутость) через диф. f(x)³f(x0)+ f‘(x0)(x-x0) "
x,x0Î(a;b) f вогнута на (а,b). Хорда выше (ниже), чем график для вып.
ф-ций (вогн.) линейная ф-ция kx+b, в частности постоянна, явл. вып. и
вогнутой.
56.Точки перегиба графика ф-ии(опр,признаки)
Опр. Т-ки разд. интервалы строгой выпуклости и строгой вогнутости наз-ся т-ми
перегиба т. х0 есть т-ка перегибы, если f‘‘(x0)=0 и 2-я пр-ная меняет знак при
переходе через х0=> в любой т-ке перегиба f‘(x) имеет локальный экстремум.
Геометр. т-ка перегиба хар-ся тем что проведенная касат. в этой т-ке имеет т-
ки графика по разные стороны.
57.Достаточное усл. Точек перегиба
58.Ассимптоты графика: вертика, гор, накл. Геом смысл накл ассимптоты.
В некоторых случаях, когда график ф-ии имеет бесконечные ветви, оказывается,
что при удалении точки вдоль ветви к бесконечности, она неограниченно
стремится к некоторой прямой. Такие прямые называют асимптотами.
.Вертикальные асимптоты – прямая 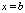
называется вертикальной асимптотой графика ф-ии 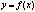
в точке b , если хотя бы один из разносторонних пределов равен
бесконечности.
Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота
появляется в тех точках, когда знаменатель равен нулю, а числитель не равен
нулю.
********************
Наклонная асимптота – прямая 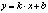
наклонная асимптота ф-ии 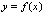
, если эта ф-ия представлена в виде 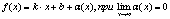
Необходимый и достаточный признак существования наклонной асимптоты:
Для существования наклонной асимптоты 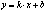
к графику ф-ии 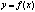
необходимо и достаточно существование конечных пределов:
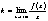 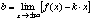
Доказательство: Пусть:
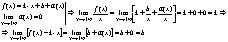
Пусть:
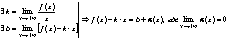
Следовательно существует асимптота.
Страницы: 1, 2, 3
| 


