|
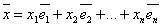

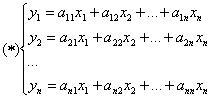
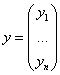 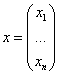 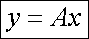
Линейное преобразование – матрица линейного оператора.
Каждому линейному преобразованию соответствует 1 матрица линейного оператора
и наоборот.
Если имеется квадратная матрица 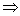 задано линейное преобразование пространства. задано линейное преобразование пространства.
17. Связь между координатами одного и того же линейного оператора в
разных базисах.
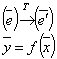
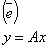 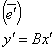
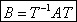
Т – матрица перехода от e к e’ , то:
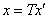 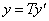
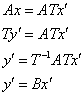
Если линейный оператор имеет в базисе невырожденную матрицу Т, матрица этого
оператора в любом другом базисе не будет вырождена.
18. Характеристическое уравнение линейного оператора. Собственные
векторы линейного оператора и их свойства.
Если в базисе 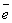
линейный оператор имеет матрицу А, а в базисе (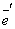
) оператор имеет матрицу В 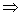
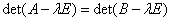
λ – произвольное число ≠0
Е – единичная матрица
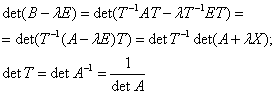
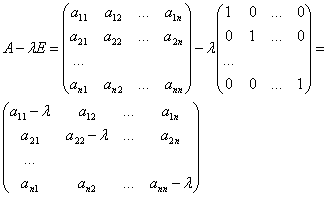 Если Если
характеристически многочлен линейного оператора прировнять к 0, получим
характеристическое уравнение линейного оператора.
Собственные векторы линейного оператора
Ненулевой вектор 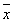
называется собственным вектором линейного оператора, если 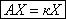
оператор к 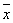 , получим , получим
этот же 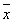 , ,
умноженный на некоторое к.
к – собственное число оператора А=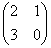
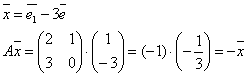
Каждый собственный вектор имеет единственное собственное число.
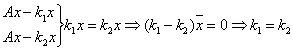
19. Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.
Векторное уравнение прямой.
Положение прямой можно задать по точке и направляющему вектору.
Пусть прямая L задана ее точкой M0(x0;y0;z
0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z).
Обозначим радиус-векторы точек M и M0 через r и r0.
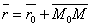
Тогда уравнение прямой запишется в виде: 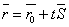
где t – скалярный множитель (параметр).
Параметрические уравнения прямой.
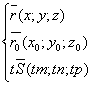
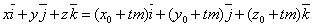
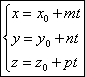
Канонические уравнения прямой.
S(m;n;p) – направляющий вектор прямой L. M0(x0;y0
;z0) – точка на прямой. 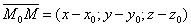
соединяет M0 с произвольной точкой М.
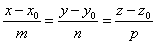
Уравнение прямой в пространстве, проходящей через две точки.
M1(x1;y1;z1) M2(x2;y2;z2)
В качестве направляющего вектора можно задать вектор 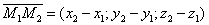
Следовательно:
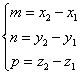 , тогда , тогда 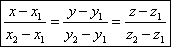
Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
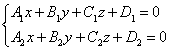 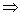 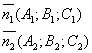
Т.к. прямая перпендикулярна векторам n1 и n2 то
направляющий вектор запишется как векторное произведение:
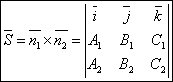
Угол между прямыми.
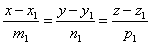 ; ;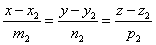
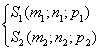
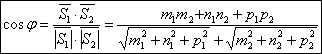
20. Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному
вектору.
Пусть плоскость задана точкой M0(x0;y0;z0
) и вектором 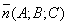 , ,
перпендикулярной этой плоскости.
Возьмем произвольную точку M(x;y;z) и составим вектор 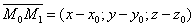
. При любом расположении точки М на плоскости Q 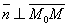
, поэтому 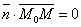 . .
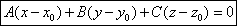
Общее уравнение плоскости.
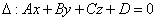
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)
· Если С=0 то вектор 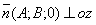
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то
ox.
· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.
Аналогично при A=D=0 и B=D=0.
· Если А=В=0 то уравнение примет вид 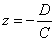 плоскость параллельна плоскости Oxy. плоскость параллельна плоскости Oxy.
· Если A=B=D=0, то уравнение имеет вид 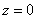 . Это уравнение плоскости Oxy. . Это уравнение плоскости Oxy.
Уравнение плоскости, проходящей через три точки
К (х1;у1) М (х2;у2) N (x3;y3)
Возьмем на плоскости точку P (x;y;z).
Составим векторы:
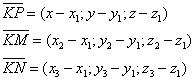
Эти векторы лежат в одной плоскости, следовательно они компланарны:
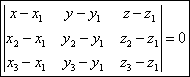
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
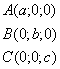 ; ; 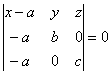 ; ; 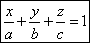
Нормальное уравнение плоскости.

21. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
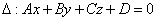
Прямая L: 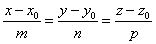
Пусть φ – угол между плоскостью и прямой.
Тогда θ – угол между 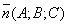 и и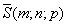 . .
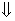
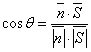
Найдем 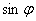 , если , если 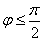
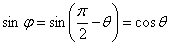 , т.к. , т.к. 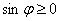
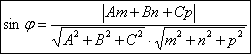
Расстояние от точки до плоскости.
Дано:
M0 (x0;y0;z0)
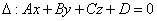
Расстояние d от точки М0 до плоскости ∆ равно модулю проекции
вектора 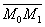 (где М (где М
1(x1;y1;z1) - произвольная точка
плоскости) на направление нормального вектора 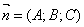
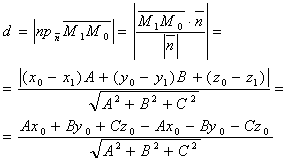
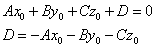
Страницы: 1, 2, 3, 4, 5
| 


