|
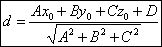
!!!Если плоскость задана уравнением:
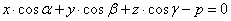
то расстояние до плоскости находится по формуле:

22. Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между
двумя прямыми.
Уравнение с угловым коэффициентом.
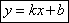
k= tg α – угловой коэффициент.
Если b=0 то прямая проходит через начало координат. Уравнение примет вид 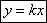
Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох. 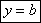
Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет
вид 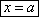 и пройдет и пройдет
параллельно оси оу.
Общее уравнение прямой.
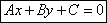
A, B, C – произвольные числа, причем А и В не равны нулю одновременно.
· Если В=0, то уравнение имеет вид 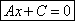
или 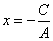 . Это уравнение . Это уравнение
прямой, параллельной оси оу. и проходящей через точку 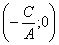
· Если В≠0, то получаем уравнение с угловым коэффициентом 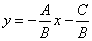 . .
· Если А=0, то уравнение имеет вид 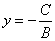 . Это уравнение прямой, параллельной оси ох. . Это уравнение прямой, параллельной оси ох.
· Если С=0, то уравнение проходит через т. О (0;0).
Уравнение прямой, проходящей через точку, в данном направлении.
т М (х0;у0).
Уравнение прямой записывается в виде 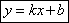 . .
Подставим в это уравнение точку М 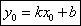
Решим систему:
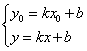 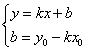
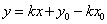
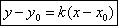
Уравнение прямой, проходящей через 2 точки.
К (х1;у1) М (х2;у2)

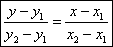
Уравнение прямой в отрезках.
К (а;0); М (0;b)
Подставим точки в уравнение прямой:
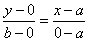
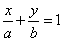
Уравнение прямой, проходящей через данную точку, перпендикулярно данному
вектору.
М0 (х0;у0). 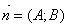
Возьмем произвольную точку М (х;у).
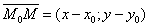
Т.к. 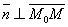 , то , то 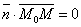
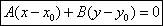
Нормальное уравнение прямой.
Уравнение прямой можно записать в виде:
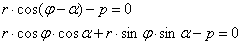
Т.к. 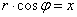 ; ;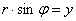 , то: , то:
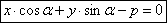
Угол между прямыми.
Дано: прямые L1 и L2 с угловыми коэффициентами
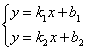
Требуется найти угол между прямыми:
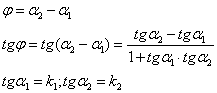
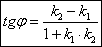
23. Эллипс. Определение. Вывод канонического уравнения.
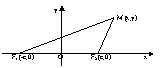 Эллипсом называется Эллипсом называется
геометрическое место всех
точек плоскости, сумма
расстояний от которых до
до фокусов есть величина
постоянная, большая, чем расстояние между фокусами.
Пусть М (х;у) – произвольная точка эллипса.
Т.к. MF1 + MF2 = 2a
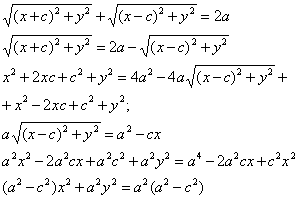
Т.к. 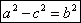
То получаем 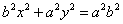
Или 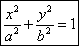
24. Гипербола. Определение. Вывод канонического уравнения.
Гиперболой называется множество всех точек плоскости, модуль разности
расстояний от каждой из которых до фокусов есть величина постоянная.
Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению
гиперболы |MF1 – MF2|=2a или MF1 – MF2
=±2a,
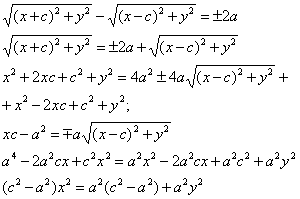
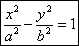 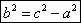
25. Парабола. Определение. Вывод канонического уравнения.
Парабола – множество всех точек плоскости, каждая из которых одинаково
удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой
называется параметром параболы и обозначается через р>0.
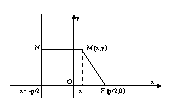 Пусть M(x;y) – произвольная Пусть M(x;y) – произвольная
точка M с F. Проведем отрезок
MN перпендикулярно
директрисе. Согласно
определению MF=MN.
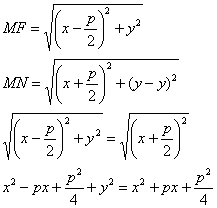
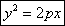
26. Поверхности вращения.
Поверхность, образованная вращением некоторой плоской кривой вокруг оси,
лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая
кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:
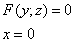
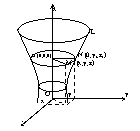 Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz. Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.
Возьмем на поверхности точку
M (x;y;z). Проведем через точку
М плоскость, перпендикулярную
оси oz, и обозначим точки
пересечения ее с осью oz
и кривой L соответственно O1 и N.
Обозначим координаты точки
N (0;y1;z1). Отрезки O1M и O1N
являются радиусами одной и той же окружности. Поэтому O1M = O1
N. Но O1M = (x2+y2)0.5, O1
N=|y1|.
Следовательно, |y1|=(x2+y2)0.5 или y1=±(x2+y2)0.5. Кроме того, очевидно, z1=z.
Следовательно 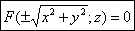 – –
искомое уравнение поверхности вращения, ему удовлетворяют координаты любой
точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на
поверхности вращения.
27. Поверхности 2-го порядка. Эллипсоид, Гиперболоид.
Эллипсоид.
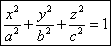
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения
таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении,
определяется двумя уравнениями:
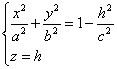
Если |h|>c, c>0, то 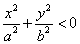 точек пересечения поверхности с плоскостями z=h нет. точек пересечения поверхности с плоскостями z=h нет.
Если |h|=c, т.е. h=±c, то 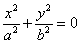
. Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и
z=–c касаются поверхности.
Если |h|<c, то уравнения можно переписать в виде: 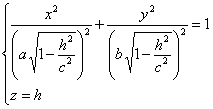
Линия пересечения есть эллипс с полуосями.
Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все
они различны, то эллипсоид называется трехосным. Если какие-либо две
полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело
называется сферой x2+y2+z2=R2
Однополостный гиперболоид.
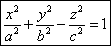
Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения
которой имеют вид.
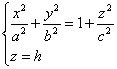 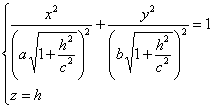
Полуоси достигают своего наименьшего значения при h=0, a1=a, b1
=b. При возрастании |h| полуоси будут увеличиваться.
Если пересекать поверхность плоскостями x=h или y=h, то в сечении получим
гиперболы. Найдем линию пересечения поверхности с плоскостью Oyx, уравнение
которой x=0. Эта линия пересечения описывается уравнениями:
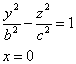
Поверхность имеет форму бесконечно расширяющейся трубки и называется
однополостным гиперболоидом.
Двуполостный гиперболоид.
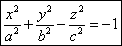
Если поверхность пересечь плоскостями z=h, то линия пересечение уравнениями
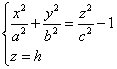
Если |h|<c, то плоскости z=h не пересекаются.
Если |h|=c, то плоскости h=±c касаются данной поверхности соответственно в
точках (0;0;с) и (0;0;-с).
Если |h|>c, то уравнения можно переписать в виде: 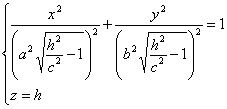
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.
У обеих гипербол действительной осью является ось oz. Метод сечения позволяет
Страницы: 1, 2, 3, 4, 5
| 


