|
|
| Диплом: К решению нелинейных вариационных задач |
Таблица 1
20
Математическая модель задачи
Обозначим через -^-количество груза, перевозимого со станции aj в пункт 6^
. Тогда общая стоимость перевозки будет + При этом Jl^t .?.
о и удовлетворяет условиям:
^ с/, х„ ^ е^ ^ ^... ^ ^з -г^ - и и е^;
(<) ^ с^ ^/
'S ^ ^CU Г ^ ^ ^ ^ •2?<5 = Ог
^ т.ч. \ ^-f-Xss. -f-^.^CLi
. ^-- ^ \ ^^Х,, =^
(2)
Л/2 + ^22 = Ьг
^ Зеез, ^ Д-^з = &
Итак: найти неотрицательное решение системы уравнений (2) дающее минимальное
значение линейной формы (1).
Решение задачи (частный случай) Пусть 0{ -- 200, Лг. = /60
^ ^ = f^O , & = 90, ^ = W,
Сн - б , С ^ = ^ С^ = 2 , С,, = S, С^ - J, ^з -= 2.
Для удобства обозначим -IV/ = :с » -^/'a :=
t/ . Тогда из (2) и условия задачи получаем следующую систему
неравенств:
Г X г0, У 7^0 , Х,л ^CL-( Х„ + Х^ ) = & - (^-+У) ^0 ' .У^^-ге^, Хаг ^&-^?^,
^2.^^^^/-^^)= ^2-^-&^ (^.^^>
В нашем случае оно примет вид:
' З^У.О^г.О Г О ^ эеf^ ^0
^у^2^ ^ ^^у^^ ^/;
^^^0,^^90 ]
/ JC^y^-У^ 1^^ ^^^У^^6?0
Тогда: -^ S^-h^^f-h 2- lsoo- (y^J -^S L W- X. J + + 3 ^^-^ + ^ L~
Юч- зе^З ш^ А зе^У + ^30 U f)
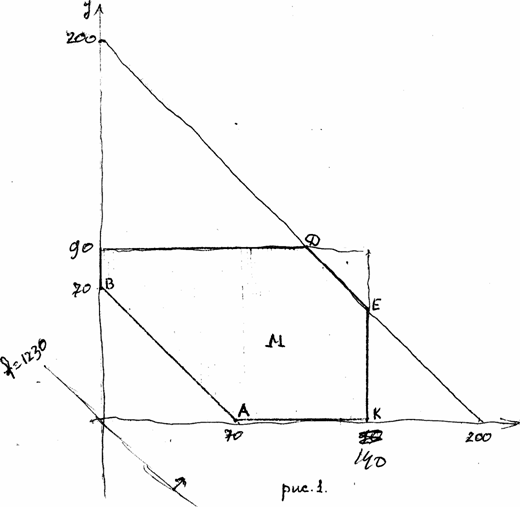
i Решение системы неравенств (2 ) будет выпуклое ограниченное
множество М. Рис. 1, а линейная форма т= х^У ^230 принимает при
этом минимальное значение на стороне C^6J множества J4., т.е. на прямой
"я^^ЧО Здесь решение задачи есть множество точек отрезка прямой Г^З
. Итак, мы можем взять любую точку на прямой х+-У= Ю . Возьмем,
например, точку A (f0',o) , т.е. 'JC-^OC^ Ю, У^О . Тогда
а?/з = ^0 , Хц ^ f0 , Лгг ^ 90, Х^ъ =0.
21
При этих значениях таблица 1 - принимает вид:
^^ь. ,4;-^ | &г | В. | Вз | Кол-во отправленного груза | А, | Ю | о | f30 | ^00 | Аг | 40 | 90 | о | /60 | | Кол-во поставленного груза | 1^0 | 90 | /зо | |
| При такой схеме перевозок затраты на них будут наименьшими и равны 1300. |
22
1.7.2. Задача о рационе
1. Поставка задачи
Пусть известно, что животному ежедневно надо выдать о^ единиц жиров
В/ , ш - углеводов Вг , V, - белков В^ . Для откорма
животных можно закупать 2 вида комбикормов. Единица веса первого корма dy
содержит <2// единицы вещества K-f , d/г. единицы вещества
В^ и <2/а единицы вещества 6э , а стоимость ее равна <?/
рубля. Для второго вида кормов данные соответственно равны 0^ , С^ц ,
<^гл и Сц . Требуется составить рацион, при котором была бы
обеспечена суточная потребность вещества вг , при чем стоимость ее была бы
наименьшей.
Все данные поместим в таблице 2.
| Виды корма | Белки | Жиры | Углеводы | Стоимость 1-й единицы | | I | ft/< 2 | CLfz 3 | ^<з ^ | ^ | | II | ^/ | CL^ tt | ^ f | е. | | 6< 6 | ^3. f2 | ^ ^ | |
Таблица 2
Математическая модель задачи
Пусть 1\- количество первого вида корма, х^ - количество второго
вида корма, получаемого животным за сутки. Так как животное может получить
питательных веществ больше нормы ^ , то очевидно:
(Ц.^^^ , '^--f^.s.
с--Г
(3)
Общая стоимость кормов, затраченных на одно животное будет:
т= C\x^C^Xs =
i^ W Итак, математическая задача формируется следующим
образом
23
Найти неотрицательное решение системы неравенств (3), дающее минимальное
значение линейной формы + = C-t з^ + Сг ^-а. . Выражение
для + называют линейной формой потому, что в него не входят члены со степенями
выше первой и произведением -с, и 3^.
Решение задачи (частный случай).
Пусть g/=6", 8>^f2, ^д=^ 0,^2 , Q^ ^, ^a ^/ ^ ^ gs.^ =^
CZ^i = / , С/ ^ Q 2 ^д. ^ ^ 3 , л? ^ д?/, js/ = •2?-2 .
Множество решений системы неравенств:
( <?^+ У >.6 2 э^ + ^у ^ ^ ^^1 + ^ ^- ^ |
есть открытый многоугольник А - (рис.2)
Среди всех точек этого множества нужно найти такую, координаты которой
минимизируют линейную форму +=с^5х+ о, -5 У . Если зафиксировать
какое-нибудь значение выражения -f= С , то получим линейное уравнение с
двумя неизвестными ^S-sa-O^y^c ^ график которого есть прямая. При
изменении от ~т>одо оо прямая o^v.-t-Qb'd^c , смещаясь параллельно
самой себе, "зачертит" всю плоскость. При некотором значении с = С/ эта прямая
достигнет многоугольника М в точке В • Очевидно, в этой точке
-f примет наименьшее значение. Координаты точки В, находим решив систему:
Г 2 х- i-y ^ G
i <?г ^ ^ = /'<?
Итак, наименьшее значение линейной формы -/=<^5х-к^3^ в М.
достигается в точке в ^г; 2) Таким образом, для наивыгоднейшего откорма
животных надо брать оба вида кормов по две единицы.
24
1.7.3. Задача об оптимальном использовании сырья
1. Постановка задачи
Пусть предприятие вырабатывает продукцию двух видов П, и Лд , для чего
используется сырье трех видов S<, ^ , -?э соответственно в количествах ^ ,
^z. , ^.i . Для изготовления единицы продукции (^потребуется и/, , й& ,
^<s единиц сырья Sf , ^г. , •5л соответственно. Условно запишем это
так: П = Он S{ + Ом. 5л ч- С?/& 5д .
Аналогично допускаем , что П = Ог/ ^ у- ^ -s;? +
^^ ^з . Доход, получаемый предприятием от выпуска единицы продукции
Л< и Па равна соответственно Су и Сд. рублям. Требуется спланировать работу
предприятия так, чтобы обеспечить наибольшую прибыль. Все данные представим в
виде таблицы 3.
Таблица 3
2. Математическое описание задачи
Предположим, что нужно изготовить •3?/ единиц продукции П< и Л^ единиц
продукции П^ . На это уйдет d^ Л\ + Cf^ Xa. единиц сырья J/
i. = /, 2/3 . Принимая во внимание ресурсы предприятия, можно написать:
(2// Л'< + 0.^ ^ ^ ^/ о^ О'/ + 0<.i ^ ^ ^
(2/s Я?/ + йгд ^ ^ ^з
Общий доход выражается линейной формой ^= б< а?/ + Сл. 3?г.
Итак, требуется найти неотрицательное решение системы неравенств, дающее
максимальное значение f^ e^ ^ -^ С^Ха. Эта
задача решается аналогично задаче о рационе.
25
1.7.4. Понятие о задаче нелинейного программирования
Рассмотрим примеры решения простейших задач нелинейного программирования.
Пример 1. , Найти
минимальное и максимальное значения функции ^= (^ ~^) +
(3^ "^ ) при ограничениях С X/-^ Хл. >
- ^ \ -?гс< +3^1 ^{2 L лу s^, эс^^О
Решение:
Область допустимых решений представляет собой многоугольник АВСЕ (рис.3).
Проводя из точки М, как из центра, окружности различных радиусов, получим:
минимальное значение функции г (SZ>)=196/13 принимает в точке Ю
(24/13, 36/13), в которой окружность касается области решений. Точка ^) не
является угловой, ее координаты находят решая систему уравнений,
соответствующих прямым /Йс> и C£~ . Имеется два локальных
максимума: з ( д\ = (f-^)^ + (о-б)2 = ^•5'
;
i(^}-- C&-^)2 + (о~б)2 = Ю
6 . ^ рис.3 Пример 2 Пусть область допустимых решений остается прежней, а й-s (,Т/-^) ^ -<- ( ^й~^)2 найти минимум и максимум i . Решение: |
| Так как | 2M> i | (е) | , то вершина А есть точка глобального мак- | | симума. | \. | • | —- | — — | ---^м | | | | | | | - | / 1 | | | | | | | | / | | | | | f- | is, | | / | | | | н | \^ ^ | | | | | | | | • ^ | s | | / | | | | | ,'' | | \ | ( | | | | | | | <2> | | | | | | | /' / | | • ':; ' •-- г | | | | | | / | | ^. 1 | | | | | | / | // | | | | | | | / | / / | | | | | | | | | у | | | | | в | | / | | | | | f | \ | | f / | / / / \>•~- | | | | | | \ | .А | Г4 | .—^-^- | | | б | Г л | ч | 6 -^ | '> |
Страницы: 1, 2, 3, 4, 5
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|
