|
=y(u0) и z1ÎFo, z0ÎF0.
Возьмем последовательность {dn} положительных чисел dn ,
сходящуюся к нулю при п®¥. Для каждого dn
найдется элемент un1 из Uo, для которого rU
(иn1, и0)< dn , но rF
(zn1,z0)>= e1 , где zn
1=y(un1). Очевидно, последовательность {un
1} сходится к элементу u0. Так как zn1
принадлежат компактному на F множеству Fo, то из последовательности {z
n1} можно выбрать подпоследовательность {Z1nk
}, сходящуюся по метрике F к некоторому элементу z0 Î
F. При этом z01¹z0 , так как для
всякого nk rF(Z1nk,z0
)>= e1 , следовательно и rF(z10,z
0)>= e1 . Этой подпоследовательности {Z1n
k} отвечает последовательность элементов u1nk= j (Z
1nk) из Uo, сходящаяся к u10= j(z
10) и являющаяся подпоследовательностью последовательности
{u1n}. Так как последовательность {u1
n} сходится к и0 =j(z0), то u1
0=j(z10)=u0=j(z0) , т. е. j(z
0)= j(z10). В силу взаимной однозначности
отображения F®U z10=z0, что
противоречит ранее установленному неравенству z10¹z
0. Лемма доказана.
Эту лемму можно сформулировать короче.
Если отображение FoàUo компакта Fo на множество Uo взаимно однозначно и
непрерывно, то обратное отображение UoàFo также непрерывно.
Эквивалентность этих формулировок следует из того, что замыкание F*
0 множества Fo, компактного на F, является компактом.
Таким образом, минимизирующая последовательность {zn} в методе
подбора сходится к zT при nà¥, если:
а)zT принадлежит классу возможных решений М;
б) множество М — компакт.
Пусть оператор А непрерывен и вместо точной правой части uT
мы имеем элемент ud такой, что rU(ud,uT
)<= d, причем ud принадлежит множеству AM (образу
множества М при отображении его с помощью оператора A) и М
есть компакт. Пусть {dn} — последовательность положительных чисел
таких, что dn à0 при nàоо. Для каждого п
методом подбора можно найти такой элемент zdn , что r
U(A zdn ,ud)<=dn . Элементы
zdn будут близки к решению zT уравнения
Az=uT. В самом деле, при отображении с помощью непрерывного
оператора образ AM компакта М есть компакт и, следовательно, по
лемме обратное отображение, осуществляемое оператором A-1,
непрерывно на AM. Так как
rU(A zdn ,u)<= rU(A zn ,ud)+rU(ud,uT),
то
rU(A zdn ,uT)<=dn+d=gdn.
Из этого неравенства и из непрерывности обратного отображения АМ
à М следует, что rF(zdn ,zT
)<= e( gdn) , причем e( gdn
)à0 при gdnà0. Таким образом, при
нахождении приближения zdn к zT надо
учитывать уровень погрешности d правой части ud.
2.1.3. На основе изложенных соображений М. М. Лаврентьев сформулировал понятие
корректности по Тихонову. В применении к уравнению (2; 0,1) задача
называется корректной по Тихонову, если известно, что для точного
значения u=uT существует единственное решение zT
уравнения (2; 0,1), AzT=uT, принадлежащее заданному
компакту М. В этом случае оператор А-1 непрерывен
на множестве N=AM и, если вместо элемента uT нам известен
элемент ud такой, что rU( uT, ud
)<=d и udÎN, то в качестве приближенного решения
уравнения (2; 0,1) с правой частью u= ud можно взять элемент zd
=A-1ud . При dà0 (udÎN) zd
будет стремиться к zT. Множество F1 (F1
Ì F), на котором задача нахождения решения уравнения (2; 0,1)
является корректно поставленной, называют классом корректности. Так,
если оператор А непрерывен и осуществляет взаимно однозначное
отображение, то компакт М, к которому принадлежит zT,
является классом корректности для уравнения (2; 0,1). Таким образом, если
задача (2; 0,1) корректна по Тихонову и правая часть уравнения uÎAM,
то метод подбора с успехом может быть применен к решению такой задачи. На первый
вопрос дан исчерпывающий ответ.
Рассмотрим задачу решения интегрального уравнения Фредгольма первого рода
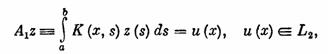 (2;1,1) (2;1,1)
на множестве М1 монотонно убывающих (возрастающих) и
равномерно ограниченных функций |z(s)|<=B. Она корректна по Тихонову, так
как множество M1 — компакт в пространстве L2.
Действительно, возьмем любую последовательность E= {z1(s), z
2(s), .... zn(s), ...} из M1. Согласно
теореме Хелли о выборе существуют подпоследовательность
E1 = {Zn1 (s), Zn2 (s), ..., Znk (s), ...},
последовательности Е и функция z*(s) из множества M1, z*(s) ÎL2, такие, что
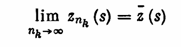
всюду, кроме, может быть, счетного множества точек разрыва функции z*(s). Из
поточечной сходимости подпоследовательности Е1 к функции
z*(s) всюду, кроме, может быть, счетного множества точек, следует, как
известно, сходимость подпоследовательности E1 к функции z*(s) по
метрике L2.
Таким образом, в качестве приближенного решения на множестве М1
уравнения (2; 1,1) с приближенно известной правой частью u1 Î
АМ1 можно брать точное решение этого уравнения с правой частью
u=u1 . Эта последняя задача эквивалентна задаче нахождения
на множестве M1 функции, минимизирующей функционал
N[z,u1]=|| A1z – u1 ||2L2 .
Пусть rU(uT, u1)<= d. Тогда, очевидно, в
качестве приближенного решения уравнения (2; 1,1) можно брать функцию zd
, для которой
|| A1zd – u1 ||2L2<= d
2 . (2;1,2)
Если заменить интегральный оператор A1z интегральной суммой на
фиксированной сетке с n узлами и обозначить значения искомой функции в узловых
точках через zi , то задача построения приближенного решения
уравнения (2; 1,1) сведется к задаче нахождения конечномерного вектора,
минимизирующего функционал N[z,и1] и удовлетворяющего
неравенству (2; 1,2).
В ряде других случаев компактные классы корректности можно указать
эффективно, что дает возможность строить устойчивые приближенные решения.
2.1.4. В силу погрешности исходных данных элемент и может не
принадлежать множеству AM. В этих условиях уравнение (2; 0,1) не имеет
решения (классического) и возникает вопрос: что надо понимать под приближенным
решением уравнения (2; 0,1)?
В этом случае вводится понятие квазирешения и метод подбора при условии
компактности множества М позволяет найти приближение к квазирешению. В
следующем параграфе вопрос о квазирешении рассматривается подробнее.
2.2. Квазирешения
2.2.1. Пусть оператор А в уравнении (2; 0,1) — вполне непрерывный.
Построение устойчивого к малым изменениям правой части и приближенного
решения уравнения (2; 0,1) по формуле
z=A-1u (2; 2,1)
возможно в тех случаях, как отмечалось в 2.1. , когда решение ищется на
компакте МÌF и правая часть уравнения принадлежит
множеству N = AM.
Обычно не существует эффективных критериев, позволяющих установить
принадлежность элемента и множеству N. Это приходится
предполагать известным априори. В практических задачах часто вместо точного
значения правой части иT нам известно ее приближенное
значение u1, которое может не принадлежать множеству N=
AM. В этих случаях нельзя строить приближенное решение уравнения (2; 0,1) по
формуле (2; 2,1), так как символ А-1u может не иметь смысла.
2.2.2. Стремление устранить затруднения, связанные с отсутствием решения
уравнения (2; 0,1) при неточной правой части, привело В. К. Иванова к
понятию квазирешения уравнения (2; 0,1) — обобщению понятия решения этого
уравнения.
Элемент z1ÎМ, минимизирующий при данном и
функционал rU(Az1,и) на множестве М,
называется квазирешением уравнения (2; 0,1) на М,
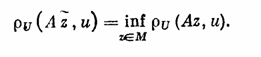
Если М — компакт, то квазирешение, очевидно, существует для любого
иÎU и если, кроме того, иÎAM, то
квазирешение z1 совпадает с обычным (точным) решением уравнения (2;
0,1). Квазирешение может быть и не одно. В этом случае под квазирешенпем будем
разуметь любой элемент из множества квазирешений D.
Можно указать достаточные условия, при которых квазирешение единственно и
непрерывно зависит от правой части и.
Напомним определение. Пусть элемент у и множество Q принадлежат
пространству U. Элемент q множества Q называется
проекцией элемента у на множество Q, q=Ру, если
выполняется равенство
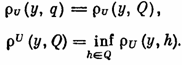
Теорема 1. Если уравнение Аz=u может иметь на компакте М не более
одного решения и проекция каждого элемента uÎU на множество N =
AM единственна, то квазирешение уравнения (2; 0,1) единственно и
непрерывно зависит от правой части u.
Доказательство. Пусть z1 — квазирешение и и1=Аz
1. Очевидно, и1 есть проекция элемента u на
множество N = AM. По условию теоремы она определяется
однозначно. Отсюда, в силу взаимной однозначности отображения множества М
на множество N, следует единственность квазирешения z1.
Очевидно, что z1 = А-1u=А-1Ри. Согласно
лемме о непрерывности обратного отображения компакта (см. предыдущий параграф)
оператор А-1 непрерывен на N. Оператор
проектирования Р непрерывен на U. Поэтому А-1P —
непрерывный на U оператор и, следовательно, квазирешение z1
непрерывно зависит от правой части и.
Таким образом, при переходе к квазирешению восстанавливаются все условия
корректности, т. е. задача нахождения квазирешения уравнения (2; 0,1) на
компакте М является корректно поставленной.
Если условие единственности решения уравнения (2; 0,1) не выполнено, то
квазирешения образуют некоторое множество D элементов компакта М.
В этом случае без упомянутых в теореме 1 ограничений на множество N
имеет место непрерывная зависимость множества квазирешений D от и
в смысле непрерывности многозначных отображений. Для случая, когда уравнение (2;
0,1) линейно, легко получить более общие результаты, содержащиеся в следующей
теореме .
Теорема 2. Пусть уравнение (2; 0,1) линейно, однородное уравнение
Az=0 имеет только нулевое решение, множество М выпукло, а всякая сфера в
пространстве U строго выпукла. Тогда квазирешение уравнения (2; 0,1) на
компакте М единственно и непрерывно зависит от правой части и.
Доказательство. Пусть z1 — квазирешение и u1=Az1
. Так как множество М выпукло, то в силу линейности оператора А
множество N=AM также выпукло. Очевидно, что и1
есть проекция элемента и на множество N. В силу того, что сфера
в пространстве U по условию теоремы строго выпукла, проекция и
определяется однозначно. Далее доказательство завершается, как в теореме 1.
2.2.3. Пусть F и U — гильбертовы пространства, МÎS
R — шар (|| z ||<=R ) в пространстве F и А — вполне
непрерывный линейный оператор.
В этом случае квазирешение уравнения (2; 0,1) можно представить в виде ряда по
собственным элементам (функциям, векторам) jn оператора А*А,
где А* — оператор, сопряженный оператору А.
Известно, что А*А — самосопряженный положительный вполне непрерывный
оператор из F в F. Пусть l1>=l2
>=.>=ln>=. — полная система его собственных значений, a j
Страницы: 1, 2, 3, 4, 5
| 


