функций С решения обратной задачи. Поэтому будем рассматривать задачу

нахождения некоторого обобщенного решения обратной задачи.

Пусть заданы число T > 0 и функция y(x), опреде­ленная в области D,

y(x) ÎL2. На функциях j(х) класса С определен

функционал

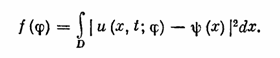
Обобщенным решением обратной задачи будем называть функцию j(х)., на

которой достигается

f0=inf f(j)

jÎC

Замечание. «Естественный» подход к решению этой задачи — выбрать функцию

j(х).так, чтобы f(j)=0 .

Для этого достаточно найти решение прямой задачи

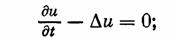
u(x, t) = 0 для х Î S, 0 < t < T;

u(x,T) = y(x)

и положить j (x) = u(x,0). Но такая задача при задан­ной функции y(x) из L2

, вообще говоря, неразрешима и, кроме того, неустойчива к малым изменениям

функ­ции y(x).

На некотором классе обобщенных функций j (x) f0=0 . Поэтому

рассматривается задача на­хождения приближенного значения f0 с

заданным уровнем погрешности.

Для заданного числа e > 0 найти функцию je(x), на которой f (je)<=e.

Эта задача и решается методом квазиобращения.

Идея метода квазиобращения состоит в том, что вмес­то оператора теплопроводности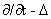

находится «близ­кий» ему оператор Вa , для которого

задача с обращением отсчета времени

Baua = 0, x Î D, t < Т, a > 0;

ua (x,T)= y(x);

ua (x,t) = 0 для xÎ S, t< Т

устойчива. Решив эту задачу, полагают j (x)=ua(x,0). Обычно в

качестве оператора Вa берут оператор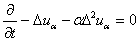

и решают прямую задачу

xÎ D, t<T, a>0;

ua (x,T)= y(x);

ua (x,t) = 0 для xÎ S, 0< t<= Т

Dua=0 для xÎ S, 0< t<= Т.

Затем полагают

j (x)=ua(x,0).

Следует отметить, что uaне сходится в обычном смыс­ле при a à0.

3.МЕТОД РЕГУЛЯРИЗАЦИИ РЕШЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ

В главе предыдущем разделе рассмотрены случаи, когда класс возможных решений

уравнения (2; 0,1) является компактом. Однако для ряда прикладных задач

характерна ситуация, когда этот класс F не является компактом, и, кроме

того, изме­нения правой части уравнения

Аz= u, (3; 0,1)

связанные с ее приближенным характером, могут выво­дить за пределы множества

AF — образа множества F при отображении его с помощью оператора

А. Такие задачи называются существенно некорректными. Был

разработан новый подход к решению некорректно поставленных задач, позволяющий

строить приближенные решения уравнения (3; 0,1), устойчивые к малым изме­нениям

исходных данных, для существенно некорректных задач. В основе этого подхода

лежит фундаментальное понятие регуляризирующего оператора (P.O.) . Для

упрощения изложения в настоящей главе мы будем полагать, что в уравнении (3;

0,1) приближенной может быть лишь пра­вая часть и, а оператор А

известен точно.

3.1. Понятие регуляризирующего оператора

3.1.1. Пусть оператор А в уравнении (3; 0,1) таков, что обратный ему оператор

A-1 не является непрерывным на множестве AF и

множество возможных решений F не является компактом.

Пусть zT есть решение уравнения Az =uT, т. е.

AzT=uT. Часто вместо uT мы имеем некоторый

элемент ud и известное число d > 0 такие, что rU(u

d,uT)<= d, т. е. вместо точных исходных данных (uT

,А) мы имеем при­ближенные исходные данные (ud, А) и

оценку их погрешности d. Задача состоит в том, чтобы по известным исход­ным

данным (ud, A, d) найти приближение zd к элементу zt

, обладающее свойством устойчивости к малым измене­ниям ud. Очевидно,

что в качестве приближенного реше­ния zd уравнения (3; 0,1) нельзя

брать точное решение этого уравнения с приближенной правой частью и= u

d, т. е. элемент zT, определяемый по формуле

zd=A-1 ud

так как оно существует не для всякого элемента u ÎU и не обладает

свойством устойчивости к малым изменениям правой части и.

Числовой параметр d характеризует погрешность пра­вой части уравнения (3;0,1).

Поэтому представляется естественным определить zd с помощью

оператора, зави­сящего от параметра, значения которого надо брать

согла­сованными с погрешностью d исходных данных ud . Эта

согласованность должна быть такой, чтобы при dà0, т. е. при приближении

(в метрике пространства U) правой части ud уравнения (3;

0,1) к точному значению uT, при­ближенное решение zd

стремилось бы (в метрике прост­ранства F) к искомому точному решению z

t уравнения AzT =uT.

Пусть элементы zT Î F и uT Î U связаны соотношением AzT = uT.

Определение 1. Оператор R(и, d), действующий из пространства U в

пространство F, называется регуля-ризирующим для уравнения

Az = и (относительно эле­мента uT), если он

обладает свойствами:

1) существует такое число d1 > 0, что оператор R(u, d) определен для

всякого d, 0<=d<=d1, и любого udÎU такого, что

rU(ud,uT)<= d;

2) для всякого e > 0 существует d0=d0(e, ud)<=d1 такое, что из неравенства

rU(ud,uT)<= d<= d0;

следует неравенство

rF(zd,zT)<= e,

где

zd=R(ud,d).

Здесь не предполагается, вообще говоря, однозначность оператора R(u,d).

Через zd обозначается произвольный элемент из множества {R(ud

,d)} значений оператора R(ud,d).

3.1.2. В ряде случаев целесообразнее пользоваться другим определением

регуляризирующего оператора (P.O.).

Определение 2. Оператор R(u, a), зависящий от параметра a и действующий из U

в F, называется регуляризирующим для уравнения Az=и

(относительно эле­мента uT), если он обладает свойствами:

1) существуют такие числа d1>0, a1>0, что опера­тор R(u, a )

определен для всякого a, принадлежащего промежутку (0, a1), и любого uÎ

U, для которого

rU(u,uT)<=d1;

2) существует такой функционал a=a(u, d), опреде­ленный на множестве Ud1

º{u; r(u,uT)<= d1} эле­ментов иÎU, что

для любого e > 0 найдется число d(e)<=d1 такое, что если u1

ÎU и rU(u1,uT)<= d<= d(e), то

rF(za,zT)<= e , где

za=R(u1, a(u1,d)).

В этом определении не предполагается однозначность оператора R(u1,

a(u1,d)). Следует отметить, что при a= d получаем

определение 1 .

3.1.3. Если rU(ud,uT)<= d, то известно, что

в качест­ве приближенного решения уравнения (3; 0,1) с прибли­женно известной

правой частью ud можно брать элемент za=R(d, a),

полученный с помощью регуляризирующе­го оператора R(u, a ), где a=a(ud

)=a1(d) согласовано с погрешностью исходных данных ud. Это решение

назы­вается регуляризованным решением уравнения (3; 0,1). Числовой параметр a

называется параметром регуляриза­ции. Очевидно, что всякий регуляризирующий

оператор вместе с выбором параметра регуляризации a, согласо­ванного с

погрешностью исходных данных ud , a=a(ud), определяет

устойчивый к малым изменениям правой час­ти и метод построения приближенных

решений уравнения (3;0,1). Если известно, что rU(ud,u

T)<= d, то согласно определению регуляризирующего оператора можно так

выбрать значение параметра регуляризации a=a(ud) ,

что при dà0 регуляризованное решение R(ud,a(ud))

стремится (в метрике F) к искомому точному ре­шению zT, т. е. r

F(zT,za(ud)). Это и

оправдывает пред­ложение брать в качестве приближенного решения урав­нения (3;

0,1) регуляризованное решение.

Таким образом, задача нахождения приближенного решения уравнения (3; 0,1),

устойчивого к малым изме­нениям правой части, сводится:

а) к нахождению регуляризирующих операторов;

б) к определению параметра регуляризации a по до­полнительной информации о

задаче, например, по величи­не погрешности, с которой задается правая часть u

d.

Описанный метод построения приближенных решений называется методом

регуляризации.

3.2. О решении вырожденных и плохо обусловленных систем линейных

алгебраических уравнений

3.2.1. Известно, с какими трудностями связано решение так называемых плохо

обусловленных систем линей­ных алгебраических уравнений: малым изменениям

пра­вых частей таких систем могут отвечать большие (выхо­дящие за допустимые

пределы) изменения решения.

Рассмотрим систему уравнений

Аz=u, (3; 2,1)

где А — матрица с элементами aij, А ={aij},

z — иско­мый вектор с координатами zj , z={zj},

и — известный вектор с координатами иi ,u= {ui

}, i, j =1, 2, ..., п. Система (3; 2,1) называется вырожденной,

если опреде­литель системы равен нулю, detA = 0. В этом случае матрица

А имеет равные нулю собственные значения. У плохо обусловленных систем

такого вида матрица А имеет близкие к нулю собственные значения.

Если вычисления производятся с конечной точностью, то в ряде случаев не

представляется возможным уста­новить, является ли заданная система уравнений

вырож­денной или плохо обусловленной. Таким образом, плохо обусловленные и

вырожденные системы могут быть не­различимыми в рамках заданной точности.

Очевидно, такая ситуация имеет место в случаях, когда матрица А имеет

достаточно близкие к нулю собственные значения.

В практических задачах часто правая часть и и эле­менты матрицы А,

т. е. коэффициенты системы (3; 2,1), известны приближенно. В этих случаях вместо

системы (3;2,1) мы имеем дело с некоторой другой системой Az=и

такой, что ||A-A||<=h, ||u-u||<= d, где смысл норм обычно определяется

характером задачи. Имея

вместо матрицы А матрицу A, мы тем более не можем высказать

определенного суждения о вырожденности или невырожденности системы (3; 2,1).

В этих случаях о точной системе Аz=u, решение которой надо определить,

нам известно лишь то, что для матрицы А и правой части и

выполняются неравенства

||A-A||<=h, ||u-u||<= d. Но систем с такими исходными данными (А, и)

бесконечно много, и в рамках извест­ного нам уровня погрешности они неразличимы.

Поскольку вместо точной системы (3; 2,1) мы имеем приближенную систему Аz=

и, то речь может идти лишь о нахождении приближенного решения. Но

приближенная система Аz=и может быть неразрешимой. Возникает вопрос:

что надо понимать под приближенным решением систе­мы (3; 2,1) в описанной

ситуации?

Среди «возможных точных систем» могут быть и вы­рожденные. Если они

разрешимы, то имеют бесконечно много решений. О приближенном нахождении

какого из них должна идти речь?

Таким образом, в большом числе случаев мы должны рассматривать целый класс

неразличимых между собой (в рамках заданного уровня погрешности) систем

урав­нений, среди которых могут быть и вырожденные, и неразрешимые. Методы

построения приближенных реше­ний систем этого класса должны быть одними и

теми же, общими. Эти решения должны быть устойчивыми к малым изменениям

Страницы: 1, 2, 3, 4, 5