|
точці х0:
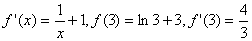
скориставшись рівнянням дотичної
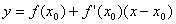 , ,
матимемо
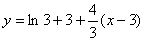
Звідси 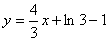 . .
Відповідь: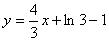 . .
Приклад 2. Який кут з віссю абсцис утворює дотична до параболи y=x2
-4x+8 в точці (3;5)?
Розв’язання. Безпосередньо підстановкою координат заданої точки в
рівняння параболи переконуємося, що вона їй належить.
Знайдемо похідну y’=2x-4.
Тоді 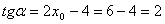 . Звідси . Звідси 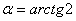
Відповідь: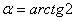
Приклад 3. Дотична до графіка функції
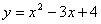
нахилена до осі абсцис під кутом 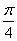 . Знайти координати точки дотику. . Знайти координати точки дотику.
Розв’язання. Знайдемо похідну функції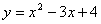 : :
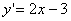 . .
За умовою y’(x0)=tg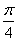 =1 маємо =1 маємо
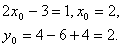
отже, дотична до параболи проходить через точку А(2;2).
Відповідь: А(2;2).
Розділ 2
Застосування похідної
2.1. Правила диференціювання
Теорема: Якщо функції u(x) і n(x) мають похідні у всіх точках
інтервалу (a; b), то
(u(x)±(x))’ = u’(x)±n’(x)
для любого х є (a; b). Коротше,
(u±n)’ = u±n’
Доведення: Суму функцій u(x)+n(x), де х є (a; b), яка представляє собою
нову функцію, позначимо через f(x) і знайдемо похідну цієї функції,
Нехай х0 – деяка точка інтервалу (a; b).
Тоді
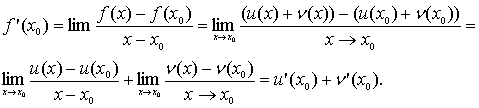

Також, 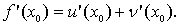
Так як
х0 – допустима точка інтервалу (a; b), то маємо:
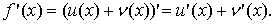
Випадок добутку розглядається аналогічно. Теорема доведена.
Наприклад,
а) 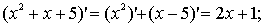
б) 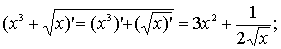
в) 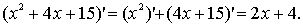
Зауваження. Методом математичної індукції доводиться справедливість
формули (u1(x) + u2 (x) +. кінцевого числа складених.
Теорема. Якщо функції u(x) і n(x) мають похідні у всіх точках
інтервалу (a; b), то
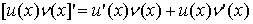
для любого х є (a; b). Коротше,
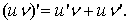
Доведення. Позначимо похідні 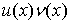
через  х є (a; b), і х є (a; b), і
найдемо похідну цієї функції, виходячи із визначення.
Нехай х0 – деяка точка інтервалу (a; b). Тоді
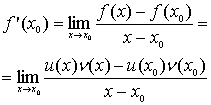
Навіть так як
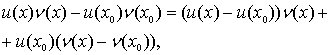
то
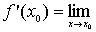 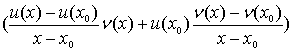
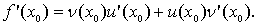
Так як х0 – вільна точка інтервалу (a; b), то маємо
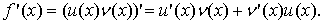
Теорема доведена.
Приклад,
а) 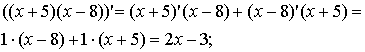  
б) 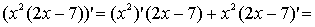
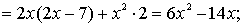
в) 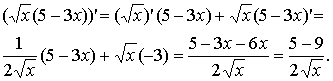
Наслідок. Постійний множник можна виносити за знак похідної:
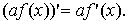
Доведення. Застосувавши множник можна виносити за знак теорему про
похідну де а – число, отримаємо
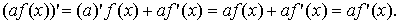
Приклади.
а) 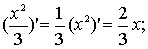
б) 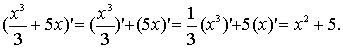
Похідна частки двох функцій .
Теорема. Якщо функції 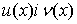
мають похідні у всіх точках інтервалу (a; b), причому 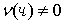
для любого х є (a; b), то
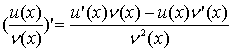
для любого х є (a; b).
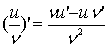
Доведення. Позначимо тимчасово 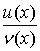
через  знайдемо знайдемо 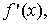
використовуючи визначення похідної.
Нехай х0 – деяка точка інтервалу (a; b).
Тоді,
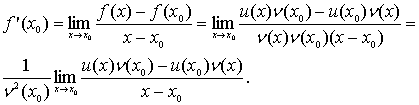
Навіть, так як
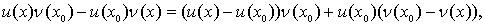
то
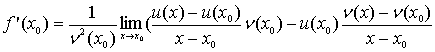
і послідовно
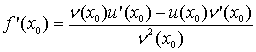
Так як х0 – вільна точка інтервалу (a; b), то в останній формулі х
0 можна замінити на х. Теорема доведена.
Приклади.
а) 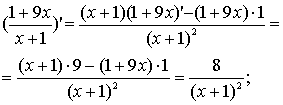
б) 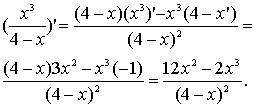
2.2. Дослідження функції та побудова графіка
Загально відомою є схема дослідження функції для побудови графіка:
1) знайти область визначення функції та множину її значень;
2) дослідити функцію на парність та непарність, періодичність;
3) знайти точки перетину графіка функції з осями системи координат, точки
розриву, проміжки знакосталості функції;
4) дослідити поводження функції біля точок розриву та на нескінченності,
знайти якщо вони є, асимптоти графіка;
5) знайти нулі та точки розриву похідної, інтервали монотонності функції,
точки екстремуму та екстремальні значення функції;
6) знайти нулі та точки розриву другої похідної, інтервали опуклості
графіка функції, точки перегину та значення функції в цих точках;
7) для побудови графіка необхідно знайти достатню кількість контрольних
точок, через які він проходить.
Зауважу, що на практиці не завжди є потреба досліджувати функцію за наведеною
схемою і в такій саме послідовності.
Так, наприклад, множину значень деяких функцій можна встановити лише після
знаходження екстремальних значень функції та її поводження біля точок розриву
і на нескінченності.
Можна спочатку знайти нулі функції. Якщо вони розташовані не симетрично
відносно нуля, то функція не може бути ні непарною, ні парною, ні
періодичною. Такий же висновок можна зробити у випадку, коли функція має
область визначення не симетричну відносно нуля, то, зрозуміло, що з такого
факту ми не можемо робити висновок про парність або непарність. Проте, якщо
нулі функції симетричні відносно нуля, але їх число скінчене, то вона не є
періодичною.
Не може бути функція ні парною, ні непарною, ні періодичною, якщо нулі першої
або другої похідних розміщені несиметрично відносно нуля.
Аналогічно можна зробити висновок і з несиметричного розміщення точок розриву.
Для складних функцій 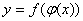 можна керуватися такими простими твердженнями: можна керуватися такими простими твердженнями:
1. якщо функція 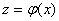 парна, то складна функція також парна; парна, то складна функція також парна;
Страницы: 1, 2, 3, 4, 5, 6
| 


