|
Зададим прямую точками М1(х1,у1) и М2(х2,у2), х1 ¹ х2. М1 и М2
принадлежат прямой, откуда следует:
у-у1=к(х-х1) для М1и у-у2=к(х-х2) для М2
откуда:
(12) Эта ф-ла позволяет вычисли ть угловой коэффициент, зная коорд двух точек.
Если у1 ¹ у2, то подставляя к из ф-лы (12) в равенство: у-у1=к(х-х1),
получаем:
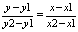 (13) Искомое уравнении прямой, проход через две заданных точки. (13) Искомое уравнении прямой, проход через две заданных точки.
28. Расстояние от точки до прямой на плоскости
Расстоянием от т. М* до прямой L наз. длину отрезка М*N – перпендикуляра L^
опущенного из т. М* на эту прямую.
Если М*(х*, у*) – заданная точка,
а 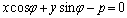 - нормальное ур-к прямой L, то расстояние от М* до L выч. по ф-ле: - нормальное ур-к прямой L, то расстояние от М* до L выч. по ф-ле:
d=d(M*,L)=|x*cosj+y*sinj-p| (14)
d=d(M*,L)=|rx×n0 -p|
обозначим через d(M*,L)= rx×n0 –p= x*cosj+y*sinj-p т. е.: d(M*,L)= |d|
по знаку d можно судить о расположении точек О и М*, относительно прямой L:
Если О и М* расположены по разные стороны относительно прямой, то d > 0 ,
если по одну сторону – то d<0. Величина d называется отклонением т. М* от
прямой L.
Если прямая задана общим уравнением, то расстояние вычисляется по ф-ле:
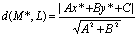
29. Уравнение прямой в отрезках
Рассматривая общее ур-е прямой, при А,В,С ¹ 0, переписав его в виде:
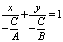 и положив и положив
а = - С/A в = - С/В получим ур-е прямой в отрезках:
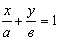 (16) (16)
Для нахождения т. М1 пересечения прямой (16) с осью ОХ достаточно решить
систему уравнений:
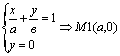
для пересечения с осью ОУ получаем:
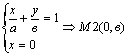
Параметры а и в в(16) определяют величину отрезков Ом1 и ОМ2, отсекаемых
прямой от осей координат.
30. каноническое уравнение прямой
Ненулевой в-р коллинеарный прямой называется ее направляющим в-ром.
Из аксиом следует, что через заданную точку проходит только одна прямая с
заданным направляющим в-ром.
Прямая L, с направл. в-ром S проходящая через т. М0(х0, у0). проходит через
т. М(х,у) тогда и только тогда, когда в-ры М0М и S 0 коллинеарны т. е.
М0М=tS, t'R) (17) Это ур-е наз векторным уравнением прямой.
Если М0(х0, у0), М(х,у) – текущие точки прямой L; S={m,n} – направляющий
вектор прямой , тогда в-р М0М = {x-x0, y-y0}
Записав условия коллинеарности из (17) в векторной форме получим: x-x0=tm, y-
y0=tn или:
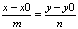 (18) Ур-е наз. каноническим ур-ем прямой на плоскости. (18) Ур-е наз. каноническим ур-ем прямой на плоскости.
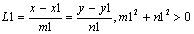 Обозначает лишь Обозначает лишь
пропорциональность и в случае, когда m = 0 или n = 0 равносильно ур-ям: х-х0=0
или у-у0=0 соответственно.
31. 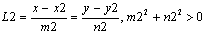 Параметрическое уравнение прямой на плоскости. Параметрическое уравнение прямой на плоскости.
Представляет собой другую форму записи ур-я (17)
пусть r=ОМ, а r0=OM0 – радиус в-ры точек М и М0 относительно начала
координат, тогда М0М = r-r0 и ур-е (17) зап. в виде: r=r0+tS, t'R
или в координатной форме, в системе ОХУ:
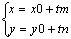 (20), t'R (20), t'R
ур-я (19) и (20) наз параметрическими уравнениями прямой на плоскости в
векторной и координатной формах.
32. Угол между двумя прямыми на плоскости.
Условия параллельности и перпендикулярности двух прямых на плоскости
а) прямые L1 L2 заданы общими уравнениями
L1:=А1х+В1у+С1=0, А12+В12>0
L2:=А2х+В2у+С2=0, А22+В22>0
j(угол между ними)= углу между их нормальными в-рами n1 ={A1,B1} и n2={A2,B2}
оттуда вытекает, что
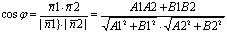
L1|| L2 Û n1 || n2Û n1 = ln2
A1=lA2, B1=lB2
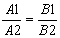
L1 ^ L2 Û n1 ^ n2Û n1×n2 =0 Û
Û A1×A2+B1×B2=0
б) прямые заданы каноническим уравнением
угол между ними равен углу между их направляющими векторами:
S1={m1,n1} S2{m2,n2} поэтому:
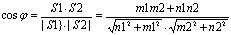 L1|| L2 Û S1 || S2 L1|| L2 Û S1 || S2
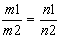
L1 ^ L2 Û S1 ^ S2 Û S1×S2=0 Û
m1×m2+n1×n2=0
в) прямые заданы ур-ем с угловым коэффициентом
L1:= у=к1х+в1
L2:= у=к2х+в2
за угол между прямыми принимаемся наименьший угол на который нужно повернуть
прямую L1 против часовой стрелки до совмещения с прямой L2 вокруг т.
пересечения прямых.
Через a1 и a2 обоз углы наклона прямых L1 и L2 к оси ОХ
Угол между прямыми j= a2- a1
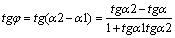
tga1=k1, tga2=k2
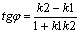
L1|| L2 Û a1 = a2 (j=0) Û k1=k2
L1 ^ L2 Û j=П/2
k2= -1/k1
33. Нормальное уравнение плоскости. Общее уравнение плоскости.
Зафиксировав неку т. О в пространстве положение плоскости П будет определено,
если задать следующие величины: расстояние до нее от начальной т. О, т. е.
длину р отрезка ОТ, перпендикуляра, опущенного из т. О на плоскость П и
единичный в-р n0, |n0|=1, перпендикулярный плоскости П и направленный из
начальной т. О к этой плоскости.
Когда текущая т. М движется по плоскости ее радиус в-р r меняется так, что
prn0 OM=p (1)
это соотношение вып для каждой т. принадлежащей плоскости, а для не
принадлежащей – нарушается.
(1) являет уравнением этой Плоскости П
prn0 OM=r×n0 или r×n0-p=0 (2)
ур-е (2) – нормальное уравнение плоскости в векторной форме. Радиус-вектор r
произвольной т. плоскости наз. ее текущим радиус вектором.
Введем в пространстве прямоугольную Декартову систему координат, поместив ее
начало в т. О, тогда в-ры r и n0 можно записать так: n0={cosa, cosb, cosd);
r={x,y,z}
Ур-е (2) примет вид:
x× cosa +y×cosb+z×cosd-p=0 (3) – нормальное уравнение
плоскости в координатной форме
Особенности ур-я (3)
1 Сумма квадратов коэффициентов при текущих координатах = 1:
cos2a+cos2b+cos2d=1
2 свободный член (-р) £0
Относительно переменных x,y,z – ур-е (3) явл. ур-ем 1 степени.
Всякое ур-е 1 степени определяет плоскость
Ур-е:
Ax+By+Cz+D=0 (4) – уравнение плоскости общего вида.
Всякий ненулевой, перпендикулярный плоскости вектор наз. нормальным вектором
этой плоскости. В-р n={A,B,C} нормальный в-р плоскости, заданной ур-ем (4),
таким образом коэффициенты при координатах в ур-е (4) являются координатами
нормального в-ра этой плоскости. Все другие нормальные вектора получают из в-
ра n умножая его на любое ¹ 0 число.
34. Ур-е плоскости проходящей через заданную точку перпендикулярно
заданному направлению
Уравнение плоскости, проходящей через т. М0, заданной r0={x0,y0,x0},
перпендикулярной в-ру n={A,B,C}строится так:
Проведем радиус в-р r={x,y,z} в произвольную т. М этой плоскости. В-р М0М=r-
r0 лежит в плоскости П и значит перпендикулярен в-ру n., поэтому их скалярное
пр-е = 0
(r-r0)×n=0 (1) Рав-во (1) справедливо для всех т. М плоскости П и
нарушается если М не принадлежит этой плоскости, тем самым – (1) – векторное
уравнение искомой плоскости, в координатной форме это выражается так:
A(x-x0)+B(y-y0)+C(z-z0)+D=0
35. Исследование ур-я плоскости. неполное ур-е плоскости
По виду общего ур-я можно судить о том как лежит плоскость относительно
системы координат OXYZ. Если хотя бы один из коэффициентов общего ур-я = 0,
то оно наз. неполным.
Возможны случаи:
1 D=0 П: Ax+By+Сz=0 т. О(0,0) удовлетворяет этому уравнению значит прямая
проходит через начало координат
2 А=0 П: Ву+ Сz +D=0 - нормальный в-р n={0,B,C} перпендикулярен оси ОХ
отсюда следует, что плоскость параллельна оси ОХ
3 В = 0 П: Aх + Cz +D=0 - нормальный в-р n={А,0,С} перпендикулярен оси ОY
отсюда следует, что плоскость параллельна оси ОУ
4 С=0 П: Ax+By+D=0, n={А,B,0} перпендикулярен OZÛП ||OZ плоскость
параллельна оси OZ
5 А=0, C=0 П: By+D=0Û y= - D/BÛ тогда из 2 П||ОХ, из 4 П||OZ
значит П||OXZ
6 А=0, В=0 П: Cz+D=0Ûz= - D/CÛ П||ОХ, П||OY значит П||OXY
7 C=0, В=0 П: Ax+D=0Û x= - D/AÛ П||ОZ, П||OY значит П||OYZ
8 A=0, В=0, D=0 П: Cz=0 Û z=0Û П||ОXY, O Î П значит П= OXY
9 A=0, C=0, D=0 П: By=0 Û y=0Û П||ОXZ, O Î П значит П= OXZ
10 B=0, C=0, D=0 П: Ax=0 Û x=0Û П||ОXY, O Î П значит П= OXY
11 A ¹ 0, В ¹ 0, С ¹ 0 П; - не параллельна ни одной из осей и
пересекает их.
36. Уравнение плоскости проходящей через три данный точки
Даны М1(x1,y1,z1), М2(x2,y2,z2), М3(x3,y3,z3) не лежащие на одной прямой.
Пусть М(x,y,z) – точка искомой плоскости.
r1={x1,y1,z1}, r2={x2,y2,z2}, r3={x3,y3,z3} и r={x,y,z} – радиус векторы
данных точек.
В силу компланарности в-ров М1М=r-r1, M1M2=r2-r1, M1M3=r3-r1 их смешанное
произведение = 0, т. е. радиус в-р т. М удовлетворяет условию:
(r-r1)(r2-r1)(r3-r1)=0 (10)
а ее координаты линейному уравнению:
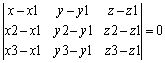 (11) (11)
ур-е (10) векторное, а ур-е (11) – координатные уравнения искомой плоскости.
37. Уравнение плоскости в отрезках.
Представив общее ур-е плоскости при A,B,C,D ¹ 0 в виде:
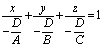
и положив a= - D/A, b = -D/B, c = -D/C, получим уравнение плоскости в отрезках:
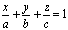
Найдем координаты точек М1, М2, М3 пересечения П с осями OX, OY, OZ
для М1 имеем
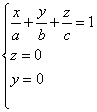
x=a, значит М1(а,0,0)
аналогично получаем:
М2(0,в,0): М3(0,0,с)
Значения а,в,с определяют величину отрезков, отсекаемых П на осях координат.
38. Расстояние от точки до плоскости
Пусть М*(x*,y*,z*) – заданная точка,
xcosa+ycosb+cosg-р=0 – заданное уравнение плоскости
расстояние от т. М* до плоскости П выч. по ф-ле:
d=d(M*, П) = |x*cosa+y*cosb+z* cosg| (13)
обозначим через d(M*, П)=r*×n0-p= x*cosa+y*cosb+z* cosg-p. Если т М* и т.
О –начало координат лежат по разные стороны от П, то d>0, а если по одну
сторону, то d<0, d - отклонение т. М* от плоскости П.
Если П задана общим уравнением, то расстояние от т. М* до П =
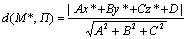
39. Угол между двумя плоскостями, условия параллельности и
перпендикулярности двух плоскостей.
П1 и П2 две заданные плоскости
П1: A1x+B1y+C1Z+D1=0
П2: A2x+B2y+C2Z+D2=0
A12+B12+C12>0, A22+B22+C22>0
углом между двумя плоскостями будем называть любой из двух смежных двугранных
углов образованных этими плоскостями. (в случае параллельности угол между ними
равен 0 или П) один из этих двугранных углов = <j между нормальными в-рами:
n1={A1,B1,C1} и n2={A2,B2,C2} этих плоскостей.
Отсюда вытекает:
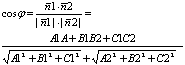
П1 || П2 Û n1 || n2 Û n1=ln2 Û A1=lА2, B1=lB2, C1=lC2
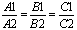 условие параллельности плоскостей условие параллельности плоскостей
П1 ^ П2 Û n1^ n2 Û n1×n2=0 Û A1A2+B1B2 + C1C2=0 условие
перпендикулярности плоскостей.
40. параметрические уравнения прямой в пространстве.
Положение прямой в пространстве будет однозначно определено, если задать т.
М0 на прямой (при помощи радиус-в-ра r0, относит некоторого фиксированного О)
и направляющего в-ра S (S ¹ 0), которому прямая параллельна.
Перемещение т. М прямой, соотв ее радиус в-ру ОМ=r ОМ=ОМ0+М0М (1)
М0М||S, M0M=t×S
r=r0+t×S (2)
Введем в пространство прямоугольную декартову систему координат, поместив
начало координат в т. О.
т. М0 имеет коорд. (x0,y0,z0); т. M (x,y,z), напр. в-р S={m,n,k}, тогда ур-е
записанное в коорд форме:
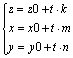 (3) (3)
Ур-я (2) и (3) наз. параметрическими уравнениями прямой в пространстве в
векторной и координатной форме соответственно. Числа m,n,k наз.
направляющими коэффициентами этой прямой.
41. Каноническое уравнение прямой в пространстве
Уравнение (2), озн. коллинеарность в-ров r-r0 и S может быть записана и в
терминах пропорциональности в-ров.
r-r0={x-x0,y-y0,z-z0}; S={m,n,k}
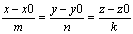 (4) (4)
Ур-е (4) наз. каноническим ур-ем прямой в пространстве, в нём x0,y0,z0 –
коорд. Т. М., лежащей на прямой, а m,n,k – координаты направляющего в-ра
прямой.
Система ур-й (4) определяет прямую, как линию пересечения двух плоскостей.
Также как и для канонического уравнения на плоскости ур-е (4) говорит лишь о
пропорциональности координат в-ров: r-r0 и S. Если например m=0, то ур-е
переходит в ур-е x-x0=0, 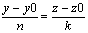
если m=0 и n=0, то у р-е будет:
x-x0=0, у-у0=0, 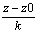
42. Уравнение прямой в пространстве, проходящей через две заданные точки
Еси на до найтить урювнение примой проход. через т. М1(x1,y1,z1) и M2(x2,y2,z2)
Для решения в каноническом виде:
Надо знать коорд одной из точек нах на прямой и направляющий в-р. За т. на
прямой можно принять любую , например, М1(x1,y1,z1), за направляющий вектор
прямой –
вектор М1М2 = {x2-x1,y2-y1,z2-z1}
Уравнение искомой прямой следует из ур-я (4):
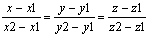 (5) (5)
43. Общее уравнение прямой в пространстве. переход к каноническим уравнениям
Всякие две непараллельные между собой и не совпадающие плоскости, определяют
прямую, как линию их пересечения.
Пусть ур-я этих плоскостей в прямоугольной декартовой системе координат OXYZ:
П1: A1x+B1y+C1z+D1=0
П2:A2x+B2y+C2z+D2=0
рассматриваемые совместно:
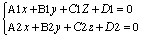 (6) (6)
Эти уравнения наз. общими уравнениями прямой L, являющийся линией пересечения
этих плоскостей. От общий уравнений прямой можно перейти к каноническим, для
этого надо знать какую-нибудь точку прямой и её направляющий вектор. точку
прямой наёдем из (6), выбирая одну из координат произвольно и решая
полученную систему относительно оставшихся 2 координат. Для отыскания
направляющего в-ра S прямой, заметим, что этот в-р, направленный по линии
пересечения данных плоскостей должен быть перпендикулярен нормальным в-рам
n1={A1,B1,C1} и n2{A2,B2,C2} так как векторное произведение n1х n2
перпендикулярно каждому из векторов n1 n2, то в качестве напр. в-ра можно
взять в-р S= n1х n2.
Найденные координаты подставляются в ур-е (4) 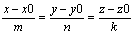
44. Угол между прямыми в пространстве. Условия параллельности и
перпендикулярности двух прямых
<j между двумя прямыми L1, L2 = углу между направляющими в-рами:S1={m1,n1,k1}
и S2={m2,n2,k2}, посему:
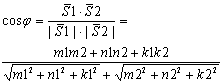 (8) (8)
Возможные случаи:
1 L1 || L2 отсюда вытекает S1 || S2
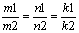 (9) (9)
2 L1 ^ L2 отсюда вытекает S1 ^ S2 = 0Û Û m1×m2+n1×n2+ к1×к2=0
45. Угол между прямой и плоскостью. Условия параллельности и
перпендикулярности прямой и плоскости.
Если дана прямая:
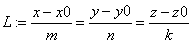
и плоскость:
П: Ax+By+Cz+D=0
<j между прямой и плоскостью называют наименьший из углов, образованных
прямой с её проекцией на эту плоскость.
Угол буде равен:
a=углу между нормальным в-ром Плоскости П n и направляющим в-ром прямой S.
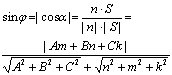
возможны случаи:
1 L || П отсюда вытекает S ^ n Û S× n = 0
Am+Bn+Ck=0 –уравнение параллельности прямой и плоскости.
2 L1 ^ L2 отсюда вытекает n || S
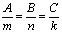 - уравнение перпендикулярности прямой и плоскости. - уравнение перпендикулярности прямой и плоскости.
Страницы: 1, 2, 3
| 


