|
|
| Методические указания: Метод наименьших квадратов |
Методические указания: Метод наименьших квадратов
10 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
10.1 Постановка задачи
Рассмотрим один из методов, позволяющих проанализировать и обработать данные,
полученные в результате эксперимента (таблица 10.1). Пусть в результате
измерений получена таблица зависимости одной величины 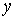 от другой
от другой 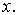 Таблица 10.1
Необходимо найти формулу
Таблица 10.1
Необходимо найти формулу 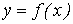 , выражающую таблично заданную зависимость аналитически. Применение интерполяции
в данном случае нецелесообразно, т.к. значения
, выражающую таблично заданную зависимость аналитически. Применение интерполяции
в данном случае нецелесообразно, т.к. значения 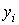 в узлах получены экспериментально и поэтому являются сомнительными (в ходе
эксперимента возникает неустранимая погрешность, обусловленная неточностью
измерений). Кроме того, совпадение значений в узлах не означает совпадения
характеров поведения исходной и интерполирующей функции. Поэтому необходимо
найти такой метод подбора эмпирической формулы, который не только позволяет
найти саму формулу, но и оценить погрешность подгонки.
Постановка задачи. Найдем функцию заданного вида
в узлах получены экспериментально и поэтому являются сомнительными (в ходе
эксперимента возникает неустранимая погрешность, обусловленная неточностью
измерений). Кроме того, совпадение значений в узлах не означает совпадения
характеров поведения исходной и интерполирующей функции. Поэтому необходимо
найти такой метод подбора эмпирической формулы, который не только позволяет
найти саму формулу, но и оценить погрешность подгонки.
Постановка задачи. Найдем функцию заданного вида
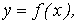 (10.1)
которая в точках (10.1)
которая в точках 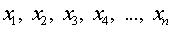 принимает значения как можно более близкие к табличным значениям
принимает значения как можно более близкие к табличным значениям 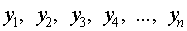 .
Практически вид приближающей функции можно определить визуально: по таблице
10.1 строится точечный график функции, а затем проводится кривая, по
возможности наилучшим образом отражающая характер расположения точек
(рис.10.1).
.
Практически вид приближающей функции можно определить визуально: по таблице
10.1 строится точечный график функции, а затем проводится кривая, по
возможности наилучшим образом отражающая характер расположения точек
(рис.10.1).
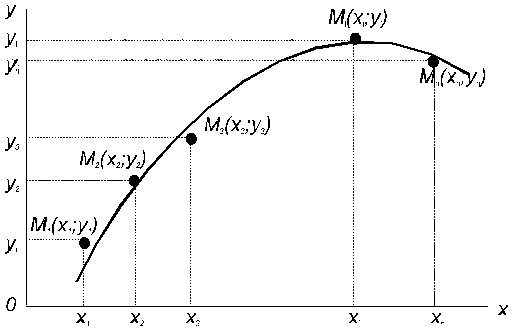 Рис.10.1
По полученной кривой устанавливается вид приближающей функции (обычно из
числа простых по виду аналитических функций: линейная, степенная,
экспоненциальная или показательная, логарифмическая, гипербола, дробно-
рациональная и т.д.).
Заметим, что формула (10.1), называемая эмпирической формулой или уравнением
регрессии
Рис.10.1
По полученной кривой устанавливается вид приближающей функции (обычно из
числа простых по виду аналитических функций: линейная, степенная,
экспоненциальная или показательная, логарифмическая, гипербола, дробно-
рациональная и т.д.).
Заметим, что формула (10.1), называемая эмпирической формулой или уравнением
регрессии 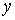 на на 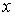 , позволяет находить значения функции
, позволяет находить значения функции 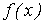 для нетабличных значений
для нетабличных значений 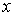 , «сглаживая» результаты измерений величины
, «сглаживая» результаты измерений величины 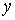 .
Из рисунка 10.1 видно, что для каждого значения
.
Из рисунка 10.1 видно, что для каждого значения 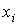 экспериментальное
экспериментальное 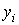 и
расчетное и
расчетное 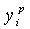 значения
различаются на некоторую величину значения
различаются на некоторую величину 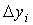 , называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных
разностей для всех точек была минимальной, найдем оптимальные параметры функции
, называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных
разностей для всех точек была минимальной, найдем оптимальные параметры функции 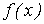 : если выполняется условие
: если выполняется условие
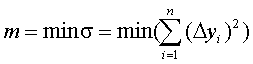 (10.2)
где (10.2)
где 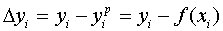 , то считается, что функция , то считается, что функция 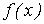 подобрана наилучшим образом.
Рассмотрим все изложенное выше на примере линейной регрессии.
10.2 Линейная регрессия
Будем искать приближающую функцию в виде: подобрана наилучшим образом.
Рассмотрим все изложенное выше на примере линейной регрессии.
10.2 Линейная регрессия
Будем искать приближающую функцию в виде:
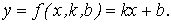 Абсолютная разность
Абсолютная разность 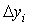 для для 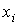 определяется следующим образом: определяется следующим образом:
 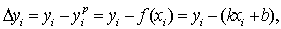 формулу (10.2) перепишем в виде:
формулу (10.2) перепишем в виде:
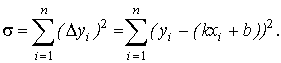 Рассматриваемая сумма является функцией с двумя параметрами
Рассматриваемая сумма является функцией с двумя параметрами 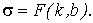 Задача сводится к отысканию минимума этой функции. Используем необходимое
условие экстремума:
Задача сводится к отысканию минимума этой функции. Используем необходимое
условие экстремума:
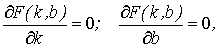 т.е.
т.е. 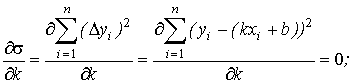 (10.3)
(10.3)
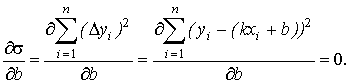 Решив систему двух уравнений с двумя неизвестными относительно параметров
Решив систему двух уравнений с двумя неизвестными относительно параметров 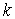 и
и 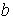 , получим
конкретный вид искомой функции , получим
конкретный вид искомой функции 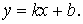 Опуская математические выкладки, запишем выражения для искомых параметров:
Опуская математические выкладки, запишем выражения для искомых параметров:
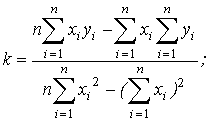 (10.4)
(10.4)
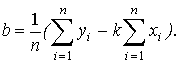 Рассчитав значение
Рассчитав значение 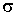 ,
получим величину среднеквадратичной ошибки рассматриваемого приближения.
Замечание: найденные значения ,
получим величину среднеквадратичной ошибки рассматриваемого приближения.
Замечание: найденные значения 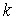 и
и 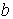 определяют точку
экстремума определяют точку
экстремума 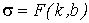 .
Используя неравенство Коши-Буняковского можно доказать, что в этой точке
функция принимает минимальное значение (см. [2]).
Как видно из рассмотренного примера, изменение количества параметров не приведет
к искажению сущности самого подхода, изменится лишь количество уравнений в
системе (10.3) (для .
Используя неравенство Коши-Буняковского можно доказать, что в этой точке
функция принимает минимальное значение (см. [2]).
Как видно из рассмотренного примера, изменение количества параметров не приведет
к искажению сущности самого подхода, изменится лишь количество уравнений в
системе (10.3) (для 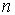 параметров соответственно будет записано
параметров соответственно будет записано 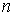 уравнений).
10.3 Подбор эмпирических формул
Чтобы подобрать формулу, выражающую зависимость между двумя величинами, если
это зависимость найдена опытным путем, строят график этой зависимости.
Полученный график сравнивают по внешнему виду с графиками, построенными при
помощи известных формул. Формулы содержат небольшое число параметров
(коэффициенты, показатели степеней и т.д.), изменением которых можно в той
или иной степени менять вид кривой. Чтобы формула не оказалась слишком
сложной, число параметров не должно быть велико. Обычно берут два-три
параметра. При сравнении обращают внимание на наличие максимумов и минимумов,
поведение функции при больших и малых значениях аргумента, выпуклость кривой
вверх или вниз на отдельных участках и т.д. Выбрав среди известных графиков
подходящий, следует подобрать такие значения параметров в формуле, чтобы
разница между опытными значениями величины и значениями, найденными по
формуле, не превышала ошибок эксперимента. Если эта разница получается
слишком большой, берут другой подходящий график и повторяют попытку.
Ниже приведены наиболее употребимые формулы и соответствующие им графики.
10.3.1 Степенная зависимость (геометрическая регрессия)
Степенная зависимость имеет вид
уравнений).
10.3 Подбор эмпирических формул
Чтобы подобрать формулу, выражающую зависимость между двумя величинами, если
это зависимость найдена опытным путем, строят график этой зависимости.
Полученный график сравнивают по внешнему виду с графиками, построенными при
помощи известных формул. Формулы содержат небольшое число параметров
(коэффициенты, показатели степеней и т.д.), изменением которых можно в той
или иной степени менять вид кривой. Чтобы формула не оказалась слишком
сложной, число параметров не должно быть велико. Обычно берут два-три
параметра. При сравнении обращают внимание на наличие максимумов и минимумов,
поведение функции при больших и малых значениях аргумента, выпуклость кривой
вверх или вниз на отдельных участках и т.д. Выбрав среди известных графиков
подходящий, следует подобрать такие значения параметров в формуле, чтобы
разница между опытными значениями величины и значениями, найденными по
формуле, не превышала ошибок эксперимента. Если эта разница получается
слишком большой, берут другой подходящий график и повторяют попытку.
Ниже приведены наиболее употребимые формулы и соответствующие им графики.
10.3.1 Степенная зависимость (геометрическая регрессия)
Степенная зависимость имеет вид
 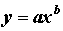 (10.5)
Во всех случаях
(10.5)
Во всех случаях 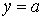 при при 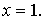 При
При 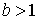 в точке в точке 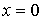 кривая касается оси абсцисс. В этом случае, чем больше
кривая касается оси абсцисс. В этом случае, чем больше 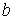 , тем ближе подходит кривая к оси абсцисс при
, тем ближе подходит кривая к оси абсцисс при 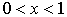 и тем быстрее она возрастает при
и тем быстрее она возрастает при 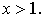 При
При 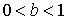 в точке в точке 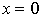 кривая касается оси ординат. При
кривая касается оси ординат. При 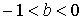 кривая ближе подходит к оси ординат, чем к оси абсцисс, при
кривая ближе подходит к оси ординат, чем к оси абсцисс, при 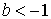 наоборот.
наоборот.
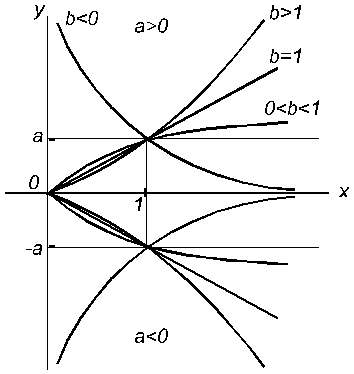 Рис. 10.2
График степенной зависимости
Покажем, как нахождение приближающей функции в виде геометрической регрессии
может быть сведено к нахождению параметров линейной функции. Предполагая, что в
исходной таблице 10.1 значения аргумента и функции положительны,
прологарифмируем равенство (10.5) при условии
Рис. 10.2
График степенной зависимости
Покажем, как нахождение приближающей функции в виде геометрической регрессии
может быть сведено к нахождению параметров линейной функции. Предполагая, что в
исходной таблице 10.1 значения аргумента и функции положительны,
прологарифмируем равенство (10.5) при условии 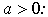
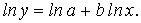 (10.6)
Введем новую переменную (10.6)
Введем новую переменную 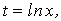 тогда
тогда 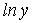 будет
функцией от будет
функцией от 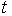 .
Обозначим .
Обозначим 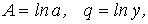 тогда
равенство (10.6) примет вид: тогда
равенство (10.6) примет вид:
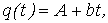 т.е. задача свелась к отысканию приближающей функции в виде линейной.
Практически для нахождения приближающей функции в виде степенной (при
сделанных выше предположениях) необходимо проделать следующие операции:
1) по данной таблице 10.1 составить новую таблицу 10.2, прологарифмировав
значения
т.е. задача свелась к отысканию приближающей функции в виде линейной.
Практически для нахождения приближающей функции в виде степенной (при
сделанных выше предположениях) необходимо проделать следующие операции:
1) по данной таблице 10.1 составить новую таблицу 10.2, прологарифмировав
значения 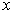 и и 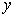 в исходной таблице;
в исходной таблице;
Таблица 10.1 | Таблица 10.2 | 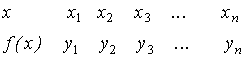
| 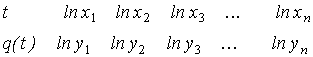
|
Страницы: 1, 2, 3
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



