Крэга «Метод определения квадратур для фигур, ограниченных прямыми и кривыми

линиями», где содержался первый и благожелательный отклик на но­вое

исчисление и применялся метод Лейбница проведе­ния касательных.

В статье Лейбница есть небезынтересные историче­ские замечания о развитии

инфинитезимальных методов в XVII в., начиная с Галилея и Кавальери. В этом

крат­ком обзоре обращает на себя внимание отсутствие име­ни Кеплера, а

заканчивается он указанием на то, что «глубочайшего дарования геометр» Исаак

Ньютон не только весьма общим образом развил метод бесконечных рядов при

определении квадратур (первый пример кото­рого дал выдающийся математик

Меркатор): вот если бы Ньютон не задерживал опубликования своих соображе­ний,

он несомненно открыл бы новые пути «для немало­го приращения науки».

Тут же Лейбниц, уже вторично в печати, выступил против того, чтобы

ограничиваться в геометрии, как то­го требовал Декарт, алгебраическими

кривыми. Лейбниц отстаивал необходимость открыть, как он выражался, источник

трансцендентных величин. А основное истори­ческое значение статьи в том, что

в ней приведены пер­вые сведения об интегральном исчислении, правда, в са­мом

кратком виде. К указанным двум статьям 1686 г. можно добавить решение

поставленной Лейбницем в 1687 г. задачи об отыскании «изохроны» (линии,

па­дая по которой тяжелая точка опускается по вертикали на равные отрезки за

равные промежутки времени) и этим будет исчерпано все, что появилось в печати

до 1690 г. о новом исчислении и его приложениях.

С 1691 по 1710 г. Лейбниц больше публикует статей и пишет писем математического

со­держания, чем в 80-е годы. То, что относится к анализу, можно собрать под

двумя рубриками: 1) новые резуль­таты, 2) обоснование анализа и полемика

с критиками, к чему в последние годы жизни Лейбница добавляется еще спор о

приоритете в открытии исчисления беско­нечно малых. Новые результаты

Лейбница достаточно разнообраз­ны. Некоторые из них относятся к технике

дифферен­цирования. Так, в «Новом методе...» 1684 г. дифферен­цируются только

алгебраические функции, рациональные и иррациональные, и, в неявном виде,

логарифм, а в 90-е годы Лейбниц, можно сказать, мимоходом в раз­личных работах

указывает дифференциалы синуса и арк­синуса, функции вида uv,

где основание и пока­затель степени - функции независимого переменного, вводит

дифференцирование по параметру. Позже Лейбниц дает носящую его имя формулу для

дифференциала лю­бого порядка от произведения функций. Можно сказать, что на

этой стадии операция дифференцирования у Лейб­ница охватила весь запас

известных тогда функций.

Другая группа результатов Лейбница относится к диф­ференциальной геометрии.

Один из наиболее существен­ных - введение огибающей семейства плоских

кривых, зависящих от некоторого параметра. Это было сделано Лейбницем

в двух статьях (1692 и 1694 гг.). К этой группе можно отнести и

замечательную работу 1693 г. «Дополнение измерительной геометрии или

выполнение в общем виде всех квадратур с помощью движения, равно как

многократное построение линий по данному условию относительно ее

касательных». Рассматривая так назы­ваемую задачу о трактрисе - о волочении

нити по плос­кости, Лейбниц совершенно четко формулирует общую идею

интеграфа, указывает условия, которым должна удовлетворять

конструкция такого прибора, и предлагает свое техническое решение,

правда, не вполне удачное.

В третью группу можно объединить результаты по интегральному

исчислению. Кроме формул, представляю­щих собой обращение упомянутых формул

дифференци­рования, Лейбниц дал две работы об интегрировании ра­циональных

дробей (1701 и 1703 гг.). В первой из них он допустил ошибку, сделав

вывод, что при наличии комп­лексных корней у знаменателя рациональной дроби с

дей­ствительными коэффициентами интегрирование должно ввести новые

трансцендентные функции, кроме обратных круговых и логарифмов. Когда же И.

Бернулли указал правильный результат, Лейбниц с ним не согласился и

повторил свое ошибочное заключение во второй работе. Эта ошибка Лейбница - не

только математический недо­смотр, она имеет любопытные корни. Утверждение,

что интегралы вида

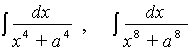
дают новые трансцендентные функции казалось ему и привлекательным и

правдоподобным еще потому, что ото соответствовало лейбницевой метафизике.

Если бы все интегралы такого вида сводились, как выражается Лейбниц, только к

квадратуре гиперболы (т. е. логарифмам) и к квадратуре круга (к обратным

круговым функциям), то все было бы единообразно. «Но природа, мать вечного

разнообразия, или, лучше сказать, божественный дух слишком цепко оберегает

свою прекрасную многоликость, чтобы допустить слияние всего в одну породу. И

таким образом он находит изящный и удивительный выход в этом чуде анализа,

этом побочном порождении мира идей, двойственном существе как бы между бытием

и небыти­ем, что мы называем мнимым корнем. И посему всякий раз, когда

знаменатель рациональной дроби имеет мнимые корни, что может получиться

бесконечно многими способами, будет мнимой и гипербола, квадратура которой

нам нужна, и ее никоим образом нельзя будет построить» . От Лейбница не

ускользнуло и то, что интеграл можно рассматривать как дифференциал с

показателем - 1, и это привело его к введению дифференциалов любых

отрицательных и дробных порядков с помощью беско­нечных рядов. Теорию

интегралов и производных дробно­го порядка развивали в XVIII в. Эйлер, в XIX

в.- Лиу-виль, Риман, Летников, в XX в. - Г. Вейль, М. Рис и др., и сейчас она

составляет один из разделов анализа. Лейбниц же первый в печати указал на то,

что операция ин­тегрирования вводит произвольную постоянную и на связь между

определением первообразной функции и квадра­турой. Он указал также, как

интегрировать некоторые типы обыкновенных дифференциальных уравнений.

Существенно то, что Лейбниц отчетливо определил взаимоотношение

интегрирования дифференциальных уравнений и интегрирования функций (первое

следует считать выполненным, если оно сведено ко второму), и, аналогично,

интегрирования функций и алгебраических операций (например, определение

корней знаменателя подынтегральной рациональной дроби считается при

интегрировании задачей решенной).

Лейбниц много занимался также интегрированием иррациональностей (в конечном

виде, как стали позже вы­ражаться) и глубоко проник в суть этой проблемы. Без

этого он не мог бы заявить, что «найдутся люди, кото­рые разнесут дальше

семена нового учения и соберут бо­лее богатую жатву, особенно тогда, когда с

большим, чем до сих пор, усердием возьмутся за развитие алгебры Дио­фанта,

которая у учеников Декарта почти в полном не­брежении, ибо они недооценивают

ее полезности в гео­метрии. Мне помнится, я уже не раз указывал на то (хотя

это может показаться удивительным), что прогресс нашего инфинитезимального

анализа в выполнении квадратур в значительной мере зависит от дальнейшего

развития той арифметики, которой, насколько нам известно; первым

целеустремленно занимался Диофант». Эти замечательные слова оправданы в

полной мере результатами Абеля, Чебышева, Золотарева, результатами,

полученными лишь в XIX в.

Заслугой Лейбница является и применение к интегрированию и функций и

дифференциальных уравнений бесконечных рядов с использованием метода

неопределенных коэффициентов (последний метод восходит к Декарту). Немалое

значение для успехов нового анализа имело достаточно общее введение такого

понятия, как функция, и систематические выступления Лейбница против

ограничения (по Декарту) предмета геометрии изучением только алгебраических

кривых. Наконец, Лейбниц на де­ле доказал достоинства своего исчисления, с

успехом участвуя в конкурсах на решение таких трудных для того времени задач,

как задача Галилея о цепной линии и задача И. Бернулли о брахистрохроне.

Были у Лейбница и попытки, которые можно оха­рактеризовать как

оппортунистические: оправдать применение бесконечно малых алгебраическими

аналогиями или сравнениями вроде того, что песчинкой можно пре­небречь по

сравнению с массой земного шара. К идее предельного перехода Лейбниц

подходит, когда рассматривает дифференциалы как потенциально исчезающие

величины; такую трактовку он использует, чтобы показать исчезновение ошибки в

конечном результате вычислений. Применял Лейбниц и свой принцип непрерывности

в такой формулировке: если явления (или данные) непрерывно сближаются так,

что в конце концов одно переходит в другое, то это же должно произойти и с

соответствую­щими последующими результатами (или искомыми). В этих трактовках

Лейбниц приближается к методам обос­нования анализа Л. Карно и Коши. Но надо

признать, что с Лейбницем мы еще целиком в мистическом периоде (определение

К. Маркса) развития математического анализа. Многие из указанных выше

результатов Лейбница были раньше известны Ньютону, медлившему с их

опубли­кованием, некоторые результаты были найдены незави­симо от Лейбница

Якобом и Иоганном Бернулли, которые к тому же значительно расширили область

применений анализа бесконечно малых в геометрии и механике, име­ют свои

заслуги в этом деле Лопиталь и Вариньон.

Но если взять отдельно сделанное только Лейбницем, то и этого достаточно,

чтобы новая математическая дис­циплина в своих основах и главных применениях

предста­ла перед современниками в почти законченном виде. Сло­вом, то, что

принадлежит Лейбницу, могло сделать его единоличным создателем исчисления

бесконечно малых.

Как ни велико сделанное Лейбницем для анализа, в анализе и с помощью анализа

бесконечно малых, этим не исчерпывается его математическое творчество. Но в

других областях математики он не мог достичь столь же значительных результатов

уже в силу самого состояния этих областей. Так, в теории чисел Лейбниц тоже

искал общий метод и, видимо, иной раз ему казалось, что он подобный метод,

какое-то регулярное исчисление нашел, но затем ему приходилось отказываться от

таких притя­заний. Результатами его поисков в этой области остались

опубликованные в 700-е годы работы по бинарной арифметике. Лейбницу принадлежит

также доказательство малой теоремы Ферма. Он интересовался и магическими

квадратами и кубами, и в последнем письме Вариньона к Лейбницу речь идет о

составленном Лейбницем магическом кубе из 27 клеток.

И в геометрии Лейбниц искал соответствующую гео­метрической сути задач

«характеристику», т. е. адек­ватную систему обозначений и действий. По этим

вопросам он ничего не опубликовал и лишь изредка касался их в переписке с

Гюйгенсом, с Лопиталем. Последнему он писал (27 декабря 1694 г.): «Я не

решаюсь еще опубликовать мои проекты характеристики положения, ибо если я не

придам ей убедительность, приведя сколько-нибудь существенные примеры, то ее

примут за фантазию. Тем не менее, я предвижу, что дело не может не удасться»

. Как указывает А. П. Юшкевич, новых конкретных ре­зультатов Лейбниц не имел

и дальнейшее развитие его гео­метрические идеи получили только в XIX в. у

Мебиуса, Штаудта, Г. Грассмана и др.

К алгебре после парижских лет Лейбниц редко обра­щался. Тут ему принадлежит

оригинальный способ иск­лючения (одной неизвестной из двух уравнений) и метод

индексации и записи результатов при решении линейных уравнений, равносильный

введению определителей. Он изложен в письме к Лопиталю 1693 г. и показан там

на примере исключения из трех линейных уравнений с тре­мя неизвестными двух

из этих неизвестных. Это дейст­вительно «первые ростки теории определителей».

Лейбница считают основоположником математической логики, и для этого есть все

основания. Конечно, он имел предшественников в XVII в. и среди них Иоахима

Юнга. О нем Лейбниц писал, что среди всех, кто когда-либо брался за

разработку истинного искусства доказа­тельства, никто так глубоко не проник в

этот предмет. Притом Юнг стремился математически рассматривать проблемы

логики и показал, что многие весьма частые в математических доказательствах

умозаключения не мо­гут быть включены в аристотелеву силлогистику. Но Лейбниц

пошел значительно дальше, стремясь, как не раз отмечалось , не только

математизировать логику, но и логизировать математику.

По Лейбницу, универсальная математика (идея Де­карта) становится истинной

формальной логикой. Ибо та­кая математика есть общая наука об отношениях, а

каж­дое отношение (например, отношение подобия в геомет­рии) может служить

основой особой теории со своими аксиомами и теоремами и соответственно

порождает осо­бое исчисление, особую алгебру. Классическая алгебра

математиков основана на отношении равенства, алгебра тождества и включения

охватывает силлогическую логи­ку и т. д., и все эти алгебры основаны на

формально определяемых правилах действий над теми или иными символами.

И Лейбниц многократно предпринимал попытки по­строить логические исчисления.

Соответствующие наброски и отрывки уже предназначавшихся для печати, но

оставшихся незаконченными работ составляют немалую долю ганноверского архива

Лейбница и содержат ряд интересных результатов и плодотворных идей. Так,

Лейбниц применил арифметическую модель - составление сложного числа из

простых множителей - для представления образования сложных понятий из простых

- идея, использованная в математической логике XX в., и, следуя по такому

пути, дал арифметическую интерпретацию логики силлогизма.

Стремясь к созданию логического исчисления, он затем перешел к алгебраизации

логики, вводя операции логического умножения и деления, логического сложения

и вычитания. Вполне последовательной алгебры логики Лейбниц все же не

построил и не только потому, что он не смог уделить этой проблеме достаточно

времени и сил: большим препятствием было то, что он сразу ста­вил перед собой

слишком трудную и обширную задачу, не расчленяя ее на более легкие и частные.

Действительно, он одновременно и расширял предмет традици­онной логики,

включая в него то, что составляет ис­числение предложений, теорию классов и

даже вероят­ностную логику, и строил для расширенной таким обра­зом логики

исчисление, пытаясь ввести сразу и прямые (сложение и умножение) и обратные

операции (вычи­тание и деление).

В итоге «не все в логической программе Лейбница выдержало испытание временем.

Развитие современной науки показало, в частности, принципиальную

неосуществимость его «всеобщей характеристики». Несостоятельной оказалась эта

типично метафизическая концепция Лейбница о сведении всего содержательного

человеческого мышления к определенному конечному чиклу формальных

математических исчислений. Провалились, естественно, и вытекающие из этой

концепции следствия, в частности, попытка Лейбница вложить вето

содержательную математику в узкие рамки формальной логики.

Однако лейбницева идея об алгебраизации задач естествознания получила

блестящую реализацию в ходе поступательного развития современной науки и

практики». В переписке и неопубликованных фрагментах Лейбница можно найти еще

немало интересных замечаний по поводу математики.

Заключение

Не раз, говоря о Лейбнице-математике, прежде всего выделяли в его даровании

силу абстрактного и обобщающего мышления. В этом отношении он действительно

превосходит всех своих современников и ближе к науке XX в., чем к науке XVII

в. И не раз, ссылаясь на некоторые ошибки Лейбница и на его собственные

заявления, занижение, на наш взгляд, оценивали Лейбница-геометра,

алгебраиста, аналитика. Изложенное выше дает достаточный материал для того,

чтобы признать Лейбница и здесь одной из замечательных фигур в историй

математики.

Чем больше мы узнаем о Лейбнице, чем основательнее обрабатываются его архив и

другие надежные источники, тем больше подтверждается достоверность

приведенного описания его дел и дней. В таких условиях мог продолжать творить

и давать значительные результаты только математический гений. И именно в

математике Лейбниц достиг вершин своего творчества. Историческое значение

математического творчества Лейбница огромно. Оно длилось около сороки лет, и

за такой сравнительно небольшой срок математика преобразилась. Наука, в

которую вступил Лейбниц, и наука, которую он оставил, принадлежат разным

эпохам, и это плод главным образом его трудов и трудов его школы. До Лейбница

в обширную область неведомого пытались проникнуть то тут, то там, наскоками,

пусть порою очень удачными, не имея общего плана. Благодаря Лейбницу

разрозненные прежде усилия были подчинены общей программе, прояснились и

близкие и далекие цели, средства для их достижения оказались в распоряжении

не только сверходаренных одиночек и значительно выиграли в эффективности.

Синтез Декарта - объединение алгебры и геометрии, давший аналитическую

геометрию, был заменен гораздо более широким синтезом - созданием анализа

бесконечно малых, который сделал полноправной дифференциальную геометрию,

воистину открыл «источник трансцендентных величин», позволил механике обрести

язык, которого ей не хватало.

Математика и математическое естествознание XVIII в. добивались своих успехов,

следуя за Лейбницем. Многие его идеи были оценены и развиты еще позже, в XIX

л XX вв. И не так давно Норберт Винер писал, что если бы кибернетика

нуждалась в святом покровителе, им надо было бы признать Лейбница.

Страницы: 1, 2, 3, 4