|
|
| Реферат: Производная и ее применение в алгебре, геометрии, физике |
|
/td> |
2. α =1—х и β=1— x2 —бесконечно малые, если
х→1. Отношение β/α=(1- x2)/(1-x) = 1+x.
Значит, 1—х и 1—x2 —бесконечно малые одинакового порядка малости при х→1.
3. Сравним 1 —cosx с х при x→ 0.
| | lim((1-cosx)/x) = lim((2sin2(x/2))/x) = lim((sin(x/2))*sin(x/2)/(x/2))= x→0 x→0 x/2→0 =lim((sin(x/2))/(x/2))*lim(sin(x/2)) = 1*0 = 0 x/2→0 x/2→0 |
|
т. е. 1—cos x при х → 0 есть бесконечно малая высшего
порядка малости, чем х.
Дифференциал функции
1°. Определение. Дифференциалом (dy) функции y=f(x) называется
произведение значения производной f '(х) на произвольное приращение ∆x
аргумента х, т. е.
(I)
2°. Для получения значения дифференциала функции необходимо знать два
числа: начальное значение аргумента, х, и его приращение, ∆x
.
Пример. Вычислить дифференциал функции у = x2 при изменении
значения аргумента х от 3 до 3,1.
Решение. dy=f '(х)* ∆х. Найдем dy сначала для произвольных
значений х и ∆x.
f '(x) = (x2)' =2x.
Поэтому
dy=2x*∆x.
Начальное значение аргумента х=3, приращение его ∆x = 3,1 — 3
= 0,1. Подставляя эти значения в выражение dy находим:
dy =2*3*0,1=0,6.
 Для данного значения
независимого переменного х дифференциал функции f(x) есть линейная функция
приращения независимого переменного ∆х.
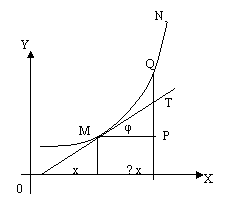
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в
точке х проведена касательная к графику функции y=f(x). Из
∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается
приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны
между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например,
если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х
от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆
x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy
= 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное
значение ∆у, имеем: абсолютная погрешность приближения равна
разности ∆у—dy=0,01, а относительная погрешность приближения есть
отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy,
высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела
f '(x) на бесконечно малую α, причем α → 0
при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x=
α, Для данного значения
независимого переменного х дифференциал функции f(x) есть линейная функция
приращения независимого переменного ∆х.
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в
точке х проведена касательная к графику функции y=f(x). Из
∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается
приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны
между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например,
если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х
от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆
x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy
= 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное
значение ∆у, имеем: абсолютная погрешность приближения равна
разности ∆у—dy=0,01, а относительная погрешность приближения есть
отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy,
высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела
f '(x) на бесконечно малую α, причем α → 0
при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x=
α,
| | lim((∆y-dy)/ ∆x) = lim α = 0. ∆x → 0 ∆x → 0 |
|
7°. Из сказанного следует: дифференциал функции есть
приближенное значение ее приращения с относительной погрешностью, стремящейся к
нулю вместе с приращением аргумента.
8°. Из изложенного следует, что дифференциал dy функции y=f(x)
обладает двумя свойствами:
1) dy пропорционален ∆x (dy = k∆x, где k=y');
2) отношение (∆y—dy)/∆x стремится к нулю при стремлении ∆x
к нулю.
Обратно. Если величина z обладает двумя свойствами:
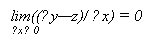 1) z=k∆x и 2) то z есть дифференциал функции у. 1) z=k∆x и 2) то z есть дифференциал функции у.
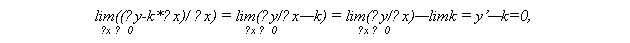 Доказательство. Внося из (1) значение z во (2), имеем:
т. е. k = y',
а следовательно,
z = k∆x = y’∆x,
т. е. z есть дифференциал функции у.
Таким образом, эти два условия полностью определяют дифференциал.
Дифференциал аргумента. Производная как отношение дифференциалов
1°. Определение. Дифференциалом (dx) аргумента х называется, его
приращение, ∆x:
dx = ∆х (II)
Может быть, некоторым основанием к этому служит то, что дифференциал функции
у=х и приращение ее аргумента совпадают. Действительно,
dy = (x)' ∆x, или dy = ∆x.
Но так как
dy = dx, то dx = ∆x,
т.е. дифференциал функции у =х и приращение ее аргумента совпадают.
2°. Внеся в формулу (I) значение ∆x=dx, получаем:
(III)
т. е. дифференциал функции есть произведение ее производной на дифференциал
аргумента.
3°. Формула (III) обладает замечательным свойством, именно: формула
dy = f '(x)dx справедлива и в том случае, если x не является независимой
переменной величиной, а является функцией другого аргумента, например и.
Действительно, если х есть функция от и, то f(x) есть
сложная функция от u приращение dx обусловлено приращением
∆u, и dy надо вычислять по формуле;
dy = f 'u (x)* ∆u.
Но
f 'u (x)= f’x (x)* x’u
Значит,
dy = f’(x)—x'u * ∆u.
Но так как, по определению,
x'u ∆u = dx,
то, следовательно,
dy = f '(x)dx.
4°. Пример. Найти дифференциал функции:
_____________________
у = √ (e2x—1).
Решение. По формуле (III)
dy = у'*dx.
Находим у':
________
________
y’ = e2x*2/( 2√ (e2x—1)) = e2x/ √ (e2x—1).
Значит
_______
dy = e2x*dx/ √ (e2x—1)
5°. Из формулы (III) следует;
f’(x)=dy/dx,
т. е. производная функции равна отношению дифференциала функции к
дифференциалу аргумента. Это иллюстрирует черт., где
dy/dx = PT/MP = tgφ=f '(x)
для произвольного значения dx = MP.
Приложения понятия дифференциала к приближенным вычислениям
1°. Разность ∆y—dy—бесконечно малая высшего порядка
малости, чем ∆x, поэтому при достаточно малом ∆x
(IV)
Это означает, что при малых изменениях аргумента (от начального значения х)
величину изменения функции y=f(x) можно приближенно считать пропорциональной
величине изменения аргумента с коэффициентом пропорциональности, равным
значению производной f '(x); кривую y=f (x) при этом можно приближенно заменить
касательной к ней в точке х.
Так как ∆у = f(х + ∆x)—f (x), то, заменяя в формуле (IV)
∆у его выражением, имеем: f(x+∆x) - f(x) ≈ f '(x)*
∆x
Доказательство. Внося из (1) значение z во (2), имеем:
т. е. k = y',
а следовательно,
z = k∆x = y’∆x,
т. е. z есть дифференциал функции у.
Таким образом, эти два условия полностью определяют дифференциал.
Дифференциал аргумента. Производная как отношение дифференциалов
1°. Определение. Дифференциалом (dx) аргумента х называется, его
приращение, ∆x:
dx = ∆х (II)
Может быть, некоторым основанием к этому служит то, что дифференциал функции
у=х и приращение ее аргумента совпадают. Действительно,
dy = (x)' ∆x, или dy = ∆x.
Но так как
dy = dx, то dx = ∆x,
т.е. дифференциал функции у =х и приращение ее аргумента совпадают.
2°. Внеся в формулу (I) значение ∆x=dx, получаем:
(III)
т. е. дифференциал функции есть произведение ее производной на дифференциал
аргумента.
3°. Формула (III) обладает замечательным свойством, именно: формула
dy = f '(x)dx справедлива и в том случае, если x не является независимой
переменной величиной, а является функцией другого аргумента, например и.
Действительно, если х есть функция от и, то f(x) есть
сложная функция от u приращение dx обусловлено приращением
∆u, и dy надо вычислять по формуле;
dy = f 'u (x)* ∆u.
Но
f 'u (x)= f’x (x)* x’u
Значит,
dy = f’(x)—x'u * ∆u.
Но так как, по определению,
x'u ∆u = dx,
то, следовательно,
dy = f '(x)dx.
4°. Пример. Найти дифференциал функции:
_____________________
у = √ (e2x—1).
Решение. По формуле (III)
dy = у'*dx.
Находим у':
________
________
y’ = e2x*2/( 2√ (e2x—1)) = e2x/ √ (e2x—1).
Значит
_______
dy = e2x*dx/ √ (e2x—1)
5°. Из формулы (III) следует;
f’(x)=dy/dx,
т. е. производная функции равна отношению дифференциала функции к
дифференциалу аргумента. Это иллюстрирует черт., где
dy/dx = PT/MP = tgφ=f '(x)
для произвольного значения dx = MP.
Приложения понятия дифференциала к приближенным вычислениям
1°. Разность ∆y—dy—бесконечно малая высшего порядка
малости, чем ∆x, поэтому при достаточно малом ∆x
(IV)
Это означает, что при малых изменениях аргумента (от начального значения х)
величину изменения функции y=f(x) можно приближенно считать пропорциональной
величине изменения аргумента с коэффициентом пропорциональности, равным
значению производной f '(x); кривую y=f (x) при этом можно приближенно заменить
касательной к ней в точке х.
Так как ∆у = f(х + ∆x)—f (x), то, заменяя в формуле (IV)
∆у его выражением, имеем: f(x+∆x) - f(x) ≈ f '(x)*
∆x
| | f(x+∆x) ≈ f(x) + f '(x)* ∆x |
|
(V)
В математике производную применяют для:
1. Исследования функции на монотонность, экстремумы.
2. Нахождения касательной к графику.
3. Нахождения наибольших, наименьших значений функций.
4. Нахождения дифференциала для приближенных вычислений.
5. Для доказательства неравенств.
Рассмотрю некоторые примеры применения производной в алгебре, геометрии и
физике.
Задача 1. Найти сумму 1+2*1/3+3(1/3)2+.+100(1/3)99;
Решение.
Найду сумму g(x)=1+2x+3x2+.+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+.+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)
2=(1—102x100+101x101)(1—x)2.
Подставлю x = 1/3.
Ответ: 0,25(9—205*3-99)
Задача 2. Найти сумму 1+2*3+3*32+.+100*399;
Решение.
Найду сумму g(x)=1+2x+3x2+.+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+.+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)
2=(1—102x100+101x101)(1—x)2.
Подставлю x = 3.
Ответ: ≈ 2,078176333426855507665737416578*1050.
Задача 3. Найдите площадь треугольника AMB, если A и
B — точки пересечения с осью OX касательных, проведенных к графику
y = (9—x2)/6 из точки M(4;3).
Решение.
т. A = укас1∩OX Решение:
т. B = укас2∩OX укас =y(x0)+у’(x0)(x—x0);
y = (9—x2)/6 y’(x0) = -2x*1/6 = -x/3;
M(4;3)________ т.к. укас проходит через M(4;3), то
SAMB —? 3 = (9—x02) — (4—x0)* x0/3 | *3
18 = 9—x02—2x0(4—x0);
x02—8 x0—9 = 0;
Д/4 = 16 + 9;
x0 = 4+5 = 9;
x0 = 4—5 = -1
укас1 = -12 — (x—9)*9/3 = -3x+15;
укас1 = 4/3 + (x+1)*1/3 = x/3+5/3;
A(5;0); B(-5;0);
AM = √10 (ед.);
AB = 10 (ед.);
BM = 3√10 (ед.);
p — полупериметр; __
p = (4√10 + 10)/2 = 2√10 + 5;
__ __ __ __ __ __
S = √(2√10 + 5) (2√10 + 5—√10
) (2√10 + 5—3√10) (2√10 + 5—10) =
= √(2√10 + 5)(√10 + 5)(5—3√10)(2√10—5) =
= √(40—25)(25—10) = 15 (ед2);
Ответ: 15 (ед2).
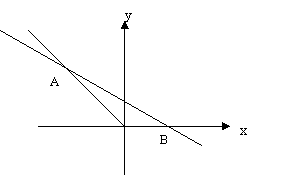 Задача 4. Какая
наименьшая плоскость может быть у треугольника OAB, если его стороны
OA и OB лежат на графике функции y = (|x|—x)/2, а прямая
AB проходит через точку M(0;1).
Решение: Задача 4. Какая
наименьшая плоскость может быть у треугольника OAB, если его стороны
OA и OB лежат на графике функции y = (|x|—x)/2, а прямая
AB проходит через точку M(0;1).
Решение:
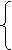 -x, x<0
y =
0, x>0
A(a;-a); B(b;0);_
AO = |a|√2 = -a√2 (т.к. a<0);
BO = b;
Для т. B:
у1 = kx +z;
т.к. у1—график линейной пропорциональности, проходящий через
т M(0;1), то z = 1.
0=kx+1;
k=-1/b;
Для т. A:
у1=kx+1;
-a=kx+1;
k=(-1-1a)/a;
у1A= у1B
(-a—a)/a = -1/b;
b+ab=a;
a(1—b)=b;
a = b/(1-b);
S∆AOB=0,5*AO*OB*sin/_AOB
ÐAOB =180o—45o = 135o
S∆AOB=0,5*(√2/2)* (-a)b√2 = -ab/2;
S∆AOB = -b2/(2(1—b)) = b2/(2(1—b))
; D(y): b>1(т.к. при b<1 не образует
∆AOB.);
т.к. функция непрерывна и дифференцируема на b>1, то найду ее производную:
S’ = (4b(b—1)—b2)/(4(b—1)2) = (4b2—4b—2b2)/(4(b—1)2) = 2b(b—2)/(4(b—1)2) =
= b(b—2)/(2(b—1)2);
S’ = 0;
точки экстремума: -x, x<0
y =
0, x>0
A(a;-a); B(b;0);_
AO = |a|√2 = -a√2 (т.к. a<0);
BO = b;
Для т. B:
у1 = kx +z;
т.к. у1—график линейной пропорциональности, проходящий через
т M(0;1), то z = 1.
0=kx+1;
k=-1/b;
Для т. A:
у1=kx+1;
-a=kx+1;
k=(-1-1a)/a;
у1A= у1B
(-a—a)/a = -1/b;
b+ab=a;
a(1—b)=b;
a = b/(1-b);
S∆AOB=0,5*AO*OB*sin/_AOB
ÐAOB =180o—45o = 135o
S∆AOB=0,5*(√2/2)* (-a)b√2 = -ab/2;
S∆AOB = -b2/(2(1—b)) = b2/(2(1—b))
; D(y): b>1(т.к. при b<1 не образует
∆AOB.);
т.к. функция непрерывна и дифференцируема на b>1, то найду ее производную:
S’ = (4b(b—1)—b2)/(4(b—1)2) = (4b2—4b—2b2)/(4(b—1)2) = 2b(b—2)/(4(b—1)2) =
= b(b—2)/(2(b—1)2);
S’ = 0;
точки экстремума:
 b=0;
b=1;
b=2;
но b>1, значит
Sнаим =S(2) = 4/(2(2—1))=2(ед2);
Ответ: 2 ед2.
Задача 5. В прямоугольном параллелепипеде ABCDA1B1
C1D1 с ребрами CD = 24, AD= 6 и DD
1 =4 проведена плоскость через центр симметрии грани A1
B1C1D1 , вершину А и точку Р
, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение
параллелепипеда этой плоскостью? На какие части делит точка P ребро
DC в этом случае?
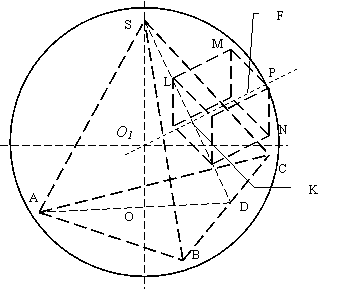
Решение. Проведем плоскость и построим сечение (рис.). АО Î АA1
C1С - линия, принадлежащая данной плоскости. Продолжим АО
до пересечения с CC1 в точке S. Тогда SP -
линия пересечения грани DD1C1C и данной плоскости,
а сечение ANMP - параллелограмм. Sсеч = SAMNP
= SK*AP/2 , потому что SK/2— высота параллелограмма ANMP.
Это видно из следующего рассуждения. b=0;
b=1;
b=2;
но b>1, значит
Sнаим =S(2) = 4/(2(2—1))=2(ед2);
Ответ: 2 ед2.
Задача 5. В прямоугольном параллелепипеде ABCDA1B1
C1D1 с ребрами CD = 24, AD= 6 и DD
1 =4 проведена плоскость через центр симметрии грани A1
B1C1D1 , вершину А и точку Р
, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение
параллелепипеда этой плоскостью? На какие части делит точка P ребро
DC в этом случае?
Решение. Проведем плоскость и построим сечение (рис.). АО Î АA1
C1С - линия, принадлежащая данной плоскости. Продолжим АО
до пересечения с CC1 в точке S. Тогда SP -
линия пересечения грани DD1C1C и данной плоскости,
а сечение ANMP - параллелограмм. Sсеч = SAMNP
= SK*AP/2 , потому что SK/2— высота параллелограмма ANMP.
Это видно из следующего рассуждения.
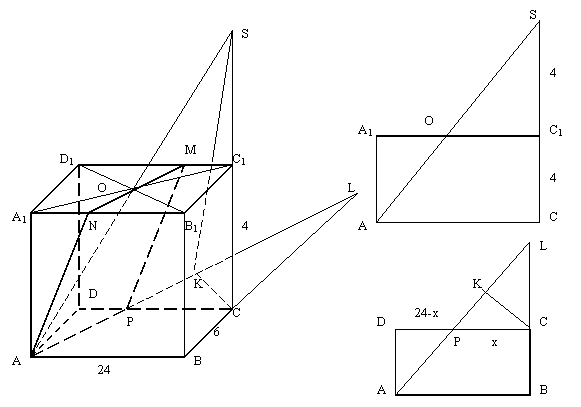 В ΔASC ОC1 - средняя линия (значит SC1 =
4), в ΔPSC также средняя линия МC1, а
плоскость A1B1C1D1 делит
пополам любую линию между S и плоскостью ABCD, а значит и
SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2
)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 =
√64+36x2/(36+(24—x)2) = 2√16+9x2
/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;
_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x
2/(36+(24—x)2) = √16(36+(24—x)2)+9x2
;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
В ΔASC ОC1 - средняя линия (значит SC1 =
4), в ΔPSC также средняя линия МC1, а
плоскость A1B1C1D1 делит
пополам любую линию между S и плоскостью ABCD, а значит и
SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2
)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 =
√64+36x2/(36+(24—x)2) = 2√16+9x2
/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;
_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x
2/(36+(24—x)2) = √16(36+(24—x)2)+9x2
;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
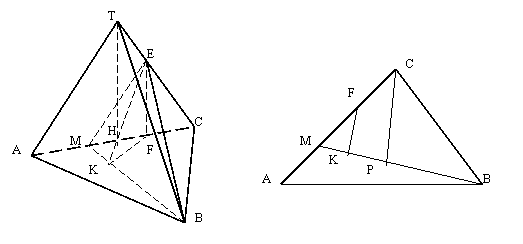 Задача 6. Высота пирамиды TABC с основанием ABC проходит
через середину ребра AC. Выберите на AC точку М так,
чтобы площадь сечения пирамиды плоскостью, проходящей через точку M,
середину ребра TC и вершину B, была наименьшей, если
AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+
EF2 = √3(x—1/2)2/(
x2—2x+4)+3/4;
_
S∆BME = 0,5√x2—2x+4
*√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)
2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
Задача 7. В сферу радиусом R вписана правильная треугольная
пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o
. Какую наименьшую площадь может иметь треугольник MBK, если точка M
лежит на апофеме пирамиды, а BK — высота основания пирамиды, не
пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
Задача 6. Высота пирамиды TABC с основанием ABC проходит
через середину ребра AC. Выберите на AC точку М так,
чтобы площадь сечения пирамиды плоскостью, проходящей через точку M,
середину ребра TC и вершину B, была наименьшей, если
AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+
EF2 = √3(x—1/2)2/(
x2—2x+4)+3/4;
_
S∆BME = 0,5√x2—2x+4
*√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)
2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
Задача 7. В сферу радиусом R вписана правильная треугольная
пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o
. Какую наименьшую площадь может иметь треугольник MBK, если точка M
лежит на апофеме пирамиды, а BK — высота основания пирамиды, не
пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
 AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
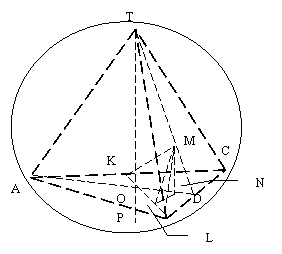
Задача 8. В сферу радиусом R вписана правильная треугольная
пирамида, высота которой в 1,5 раза меньше высоты основания. Между
боковой гранью пирамиды и сферой расположена правильная четырехугольная призма,
одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой
грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна
быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу
радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,
AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
Задача 8. В сферу радиусом R вписана правильная треугольная
пирамида, высота которой в 1,5 раза меньше высоты основания. Между
боковой гранью пирамиды и сферой расположена правильная четырехугольная призма,
одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой
грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна
быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу
радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,
Страницы: 1, 2, 3, 4, 5, 6
|
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|




 Для данного значения
независимого переменного х дифференциал функции f(x) есть линейная функция
приращения независимого переменного ∆х.
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в
точке х проведена касательная к графику функции y=f(x). Из
∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается
приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны
между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например,
если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х
от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆
x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy
= 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное
значение ∆у, имеем: абсолютная погрешность приближения равна
разности ∆у—dy=0,01, а относительная погрешность приближения есть
отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy,
высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела
f '(x) на бесконечно малую α, причем α → 0
при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x=
α,
Для данного значения
независимого переменного х дифференциал функции f(x) есть линейная функция
приращения независимого переменного ∆х.
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в
точке х проведена касательная к графику функции y=f(x). Из
∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается
приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны
между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например,
если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х
от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆
x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy
= 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное
значение ∆у, имеем: абсолютная погрешность приближения равна
разности ∆у—dy=0,01, а относительная погрешность приближения есть
отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy,
высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела
f '(x) на бесконечно малую α, причем α → 0
при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x=
α,
 Задача 4. Какая
наименьшая плоскость может быть у треугольника OAB, если его стороны
OA и OB лежат на графике функции y = (|x|—x)/2, а прямая
AB проходит через точку M(0;1).
Решение:
Задача 4. Какая
наименьшая плоскость может быть у треугольника OAB, если его стороны
OA и OB лежат на графике функции y = (|x|—x)/2, а прямая
AB проходит через точку M(0;1).
Решение:
 В ΔASC ОC1 - средняя линия (значит SC1 =
4), в ΔPSC также средняя линия МC1, а
плоскость A1B1C1D1 делит
пополам любую линию между S и плоскостью ABCD, а значит и
SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2
)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 =
√64+36x2/(36+(24—x)2) = 2√16+9x2
/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;
_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x
2/(36+(24—x)2) = √16(36+(24—x)2)+9x2
;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
В ΔASC ОC1 - средняя линия (значит SC1 =
4), в ΔPSC также средняя линия МC1, а
плоскость A1B1C1D1 делит
пополам любую линию между S и плоскостью ABCD, а значит и
SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2
)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 =
√64+36x2/(36+(24—x)2) = 2√16+9x2
/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;
_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x
2/(36+(24—x)2) = √16(36+(24—x)2)+9x2
;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
 Задача 6. Высота пирамиды TABC с основанием ABC проходит
через середину ребра AC. Выберите на AC точку М так,
чтобы площадь сечения пирамиды плоскостью, проходящей через точку M,
середину ребра TC и вершину B, была наименьшей, если
AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+
EF2 = √3(x—1/2)2/(
x2—2x+4)+3/4;
_
S∆BME = 0,5√x2—2x+4
*√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)
2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
Задача 7. В сферу радиусом R вписана правильная треугольная
пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o
. Какую наименьшую площадь может иметь треугольник MBK, если точка M
лежит на апофеме пирамиды, а BK — высота основания пирамиды, не
пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
Задача 6. Высота пирамиды TABC с основанием ABC проходит
через середину ребра AC. Выберите на AC точку М так,
чтобы площадь сечения пирамиды плоскостью, проходящей через точку M,
середину ребра TC и вершину B, была наименьшей, если
AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+
EF2 = √3(x—1/2)2/(
x2—2x+4)+3/4;
_
S∆BME = 0,5√x2—2x+4
*√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)
2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
Задача 7. В сферу радиусом R вписана правильная треугольная
пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o
. Какую наименьшую площадь может иметь треугольник MBK, если точка M
лежит на апофеме пирамиды, а BK — высота основания пирамиды, не
пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
 AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
Задача 8. В сферу радиусом R вписана правильная треугольная
пирамида, высота которой в 1,5 раза меньше высоты основания. Между
боковой гранью пирамиды и сферой расположена правильная четырехугольная призма,
одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой
грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна
быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу
радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,
AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
Задача 8. В сферу радиусом R вписана правильная треугольная
пирамида, высота которой в 1,5 раза меньше высоты основания. Между
боковой гранью пирамиды и сферой расположена правильная четырехугольная призма,
одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой
грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна
быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу
радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,