|
Теорема3. Пусть F – поле, |F|=q, тогда 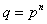 , p – простое, , p – простое, 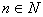 . .
Cледствие. Если F – конечное поле, то оно имеет характеристику p –
простое натуральное число, таким образом содержит подполе, изоморфное 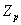
.
Теорема о примитивном корне (4). Элемент группы называется примитивным корнем,
если его степени 0,1,2,. пробегают все элементы группы. Cуть теоремы в том, что
в поле F из q элементов найдётся элемент а , что каждый ненулевой
элемент поля представляет степень а, т.е. a – примитивный
корень, и порядок элемента а равен q-1.
Теорема 5. Пусть F – поле и 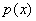
- нормализованный полином из F[х]. Тогда существует таккое содержащее F
поле K, что в К[x] полином 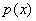
разлагается в произведение линейных сомножителей. Это поле К называют полем
расщепления для 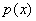 . К . К
примеру,
C – поле расщепления для любого полинома из Q[x].
Пусть 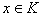 - корень - корень
некоторого ненулевого полинома из F[x]. Тогда элемент х
называют алгебраичным над F. Иначе – трансцендентным.
Теорема 6. Пусть 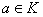
алгебраичен над F. Тогда существует единственный неприводимый
нормированный полином 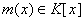
, что 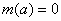 , и каждый , и каждый
полином 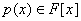 с корнем с корнем
а делится на m(x). Этот полином называют минимальным полиномом
элемента а над F.
Разложение полиномов на множители в конечных полях. Любой полином степени
n в 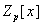 может быть может быть
разложен на множители за конечное число шагов, так как существует 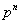
возможных полиномов степени <n, но такой алгоритм "проб и ошибок” чрезмерно
трудоёмкий(этот алгоритм осуществляется через PDF). Так что неплохо бы иметь
более быстрые алгоритмы.
Если взять полином 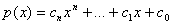
, то его производная 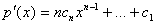
равна нулю тогда и только тогда 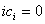
для каждого i. Это будет выполнено в случаях p|i или 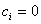
для каждого i. Поэтому 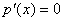
если 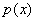 - полином от - полином от 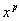
. Теперь несколько обобщим данную ранее теорему о НОД(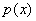
,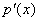 ): ):
Теорема. Пусть K - область с однозначным разложением на множители, произвольной
характеристики . И пусть 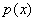
- примитивный полином в K[x], отличный от константы. Возьмём его однозначное
разложение на множители 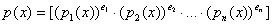
.Пусть 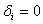 , если , если 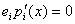
, в противном случае 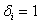
. Тогда НОД(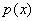 , ,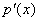
)=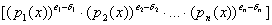 . .
Доказательство данной полностью аналогично доказательству уже доказанной
теоремы.
На этой теореме также основана некоторая модификация алгоритма PSQFF, но
перед этим нужно доказать ещё две вспомогательные теороемы.
Теорема 1. Пусть 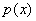 - полином в - полином в 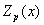 . Тогда . Тогда 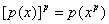 . .
Доказательство:Пусть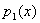 , ,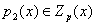 .Тогда .Тогда 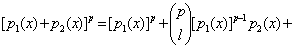
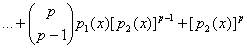 = =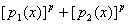
(все биномиальные коэффициенты делятся на р). Так как 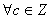 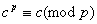
(малая теорема Ферма) то 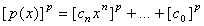
=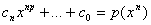 . .
Теорема 2. Пусть 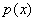 - -
полином в 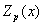 . Тогда . Тогда 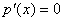
в том и только в том случае, когда p(x) eсть р-ая степень некоторого полинома 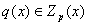
.
Доказательство:
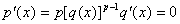 . Обратно, если . Обратно, если 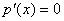 , то , то 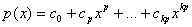 . Тогда . Тогда 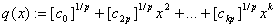 . .
Таким образом получен следующий алгоритм PSQFFF разложения на свободные от
квадратов множители над конечным полем (Polynomial Square-free
Factorization over a Finite Field) :
Вход: 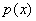 - -
нормированный полином из 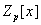
, не являющийся константой, p>0 – простое число.
Выход: 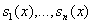 и е и е
, такие что 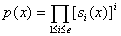 - -
разложение полинома 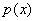
на свободные от квадратов множители.
Реализация:
BEGIN
k:=0; m:=1; e:=0 // инициализировали
label3:
j:=1; 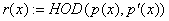 ; ; 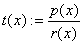
IF 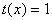 THEN GOTO label1 THEN GOTO label1
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9
| 


