|
степени n>1 неприводим в 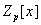
тогда и только тогда когда 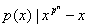
и 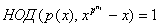 для всех для всех 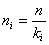
, 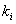 - простые - простые
делители n.
Алгоритм Берлекампа разложения на множители над конечными полями. Идея
Берлекампа основана на китайской теореме об остатках для полиномов:
Пусть 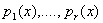 - полиномы - полиномы
из 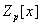 , причём , причём 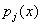
взаимно прост с 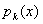 при при 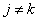
. Пусть 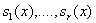 - -
произвольные полиномы из 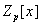
. Тогда существует единственный полином 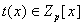
, такой что 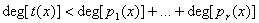 и и 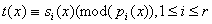
. Это же можно сформулировать на языке отображений:
Отображение, ставящее в соответствие полиному 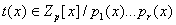
вектор 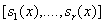 , где , где 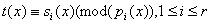
, является биекцией между 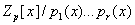
и 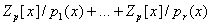 . .
Доказательство: Проводится расширенным алгоритмом Евклида. То есть определяются
полиномы 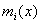 , такие , такие
что 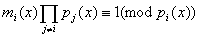 . Полагаем . Полагаем 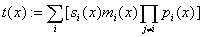
. Тогда 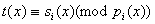 , , 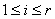
. Если бы нашёля такой 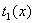
, который бы был решением этих сравнений, то полином 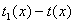
должен делиться на все 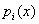
. Поэтому 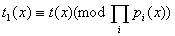 . .
Теорема. В поле GF(p) – поле Галуа (конечное поле, содержащее p (простое
число) элементов) имеет место разложение:
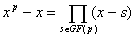 . .
Доказательство: В поле Галуа 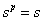
(а также по малой теореме Ферма) . Значит s является корнем полинома 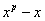
, то есть (x-s) является делителем 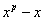
. А так как это выполнено для всех 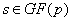
то 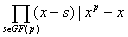 . Также следует . Также следует
заметить, что 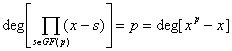 и и
это два нормированных полинома, из этого всего и следует их равенство.
Следствие. Для 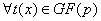 имеет место равенство: имеет место равенство:
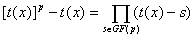 . .
Теорема. Пусть 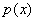 и и 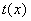 - два нормированных полинома над GF(p), такие что - два нормированных полинома над GF(p), такие что
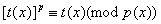 , , 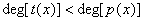 . .
Тогда 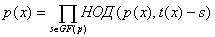
Доказательство: Из предположения следует, что 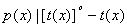 . Поэтому . Поэтому
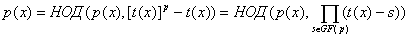
Помимо этого 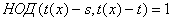 для для 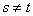 , и полиномы , и полиномы 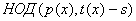 и и 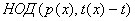 также взаимно просты. Поэтому также взаимно просты. Поэтому 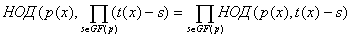 . .
Таким образом, пусть 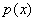
- свободный от квадратов полином степени n, который нужно разложить на множители
над GF(p), и предположим, удалось найти полиномы 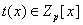
, 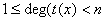 , такие что , такие что 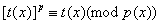
. По одной из ранее доказанных теорем, полином 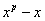
имеет в 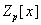 ровно p ровно p
корней. А именно 0,1.p-1. Значит он раскладывается следующим образом 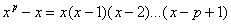
. Заменив х на 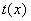 , в , в
кольце 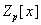 получим получим 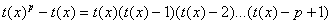
. Так как 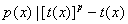 , то , то 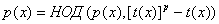
. Кроме того поскольку полиномы 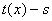
и 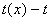 - взаимно простые - взаимно простые
при 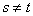 , то , то 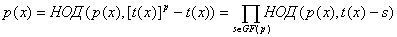
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9
| 


