|
Описание реализации:
- Построить матрицу Q.
2. Триангуляция этой матрицы. Привести матрицу Q к треугольному виду,
вычислив её ранг n-r и найдя нуль-пространство (т.е. его базис 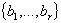
). Здесь r – число неприводимых сомножителей полинома. Так как решением
уравнения сравнения являются 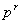
полиномов, соответствующие векторам 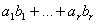
при любом выборе чисел 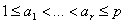
. И если r=1 то полином неприводим и алгороитм завершает работу.
3. Вычисление сомножителей. Пусть 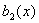
- полином, соответствующий вектору 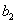
. Вычислим 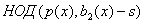 для для
всех 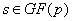 . Если с . Если с
помощью 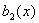 получено получено
менее r сомножителей, вычислим 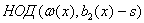
для всех 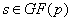 и всех и всех
сомножителей 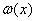 , ,
найденных к данному времени, k=3,4,.,r, пока не найдётся r сомножителей. Это
гарантируется предидущими теоремами.
На шаге 2 этого алгоритма матрица матрица Q приводится к треугольному виду,
затрачивается время 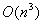
. Так как требуется не более p вычислений НОД для каждого базисного вектора и не
более r из этих вычислений будут нетривиальны, то 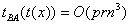
. Так что алгоритм не очень эффективен при больших p. Разберём
Пример. Разложим над GF(13) полином 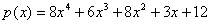 , свободный от квадратов. , свободный от квадратов.
Решение. Вместо данного полинома рассмотрим нормированный эквивалентный полином 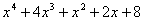
.
Для начала вычислим обратные элементы ненулевым элементам GF(13) (1,.,12).
Это соответственно будут (1,7,9,10,8,11,2,5,3,4,6,12).
Первая строка матрицы Q [4x4] всегда представляет собой (1,0,0,0), соответствуя
полиному 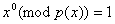 . Вторая . Вторая
строка представляет 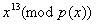
, третья 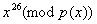 , четвёртая , четвёртая 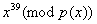
.
Пусть 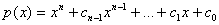 . Предположим, что . Предположим, что 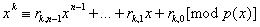 . Тогда . Тогда 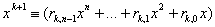 или или
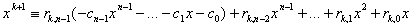
. Что означает
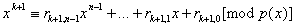 . Здесь . Здесь 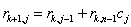 , , 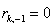 . .
Эти формулы объясняют вычисление 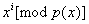
. Вычисления можно проводить используя массив 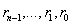
. В цикле 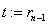 , , 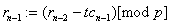
,., 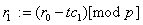 , , 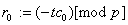
. Результаты отображаем в таблице:
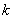
| 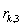
| 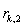
| 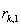
| 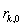
| | 0 | 0 | 0 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 2 | 0 | 1 | 0 | 0 | | 3 | 1 | 0 | 0 | 0 | | 4 | 9 | 12 | 11 | 5 | | 5 | 2 | 2 | 0 | 6 | | 6 | 7 | 11 | 2 | 10 | | 7 | 9 | 8 | 9 | 9 | | 8 | 11 | 0 | 4 | 6 | | 9 | 8 | 6 | 9 | 3 | | 10 | 0 | 2 | 0 | 1 | | 11 | 2 | 0 | 1 | 0 | | 12 | 5 | 12 | 9 | 10 | | 13 | 5 | 4 | 0 | 12 |
Нетрудно видеть вторую строку матрицы Q: (12,0,4,5). Аналогично строим для
k=26,39 и получаем матрицу
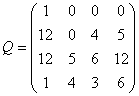 , , 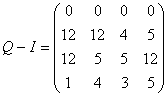 . .
Теперь нужно находить нуль-пространство матрицы Q-I. На основании
эквивалентных преобразований матрицы составляется следующий алгоритм NS
(Null-Space algorithm):
Вход: Матрица размера n 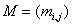 , , 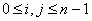 , с элементами из поля. , с элементами из поля.
Выход: Линейно независимые вектора 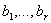 , такие что , такие что 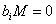 , n-r – ранг матрицы М. , n-r – ранг матрицы М.
Реализация:
- r:=0;
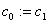 ,., ,., 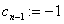
2. Для h от 0 до n-1 : если найдётся столбец с номером h и 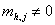
, 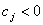 , j=0,.,n-1, то , j=0,.,n-1, то
j-тый столбец матрицы M умножаем на 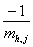
, чтобы 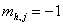 , затем для , затем для
всех 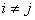 прибавляем прибавляем
умноженный на 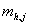
столбец j к столбцу i. И 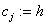
. Если не найдётся столбца j, чтобы 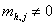
, то положить 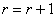 , ,
выдать вектор 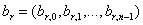 , ,
где для 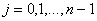
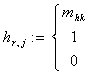
если 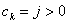 , если таких k не одно, то взять любое. , если таких k не одно, то взять любое.
если 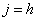
в противном случае.
При 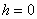 получится получится
вектор 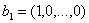 . Он . Он
соответствует полиному-константе 1. При 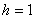
можно взять j равным 0,1,2,3, поскольку 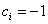
для i=1,2,3 – выбор на данном этапе полностью произволен, хотя он и влияет на
получаемые при выходе векторы. Берём j=0 и после ранее описанных преобразований
матрица Q имеет вид:
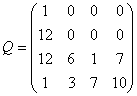 . .
Второй элемент в первом столбце 12 – означает 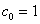 . Для h=2 матрица будет . Для h=2 матрица будет
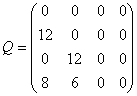 . .
Третий элемент второго столбца означает, что 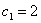
. Два последние столбца, состоящие только из нулей, обуславливают на выходе
вектор 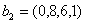 при h=3. при h=3.
Соответствующий полином будет 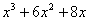
.
Из вида матрицы Q-I при h=3 видно, что векторы 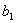
и 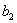 удовлетворяют удовлетворяют
условию 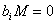 . Так как . Так как
эти вычисления дали только два линейно независимых вектора, то 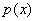
должен иметь только два неприводимых сомножителя над GF(13).
Теперь нужно переходить к третьему шагу алгоритма Берлекампа, в котором
непосредственно найдутся эти сомножители. Этот шаг состоит в нахождении 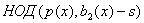
для всех 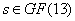 . Здесь . Здесь 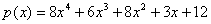
и 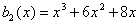 . После . После
вычислений получаем при 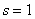 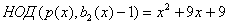
и при 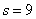 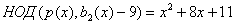
. Непосредственная проверка показывает, что полиномы найдены правильно.
Но если p достаточно велико, то алгоритм имеет огромную трудоёмкость,
связанную с вычислением НОДов для всех 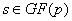
. Лучший способ вычислений был предложен Кантором и Пассенхаузом, и с ними мне
предстоит разобраться в следующей курсовой работе.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9
| 


