|
, значение ArgZ не определено, а при 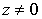
оно определено с точностью до кратного 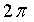
. Упомянутая ранее формула Эйлера позволяет записать число z в виде 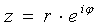
(показательная форма комплексного числа).
Геометрическое истолкование комплексных чисел позволило определить многие
понятия, связанные с функцией комплексного переменного, расширило область их
применения.
Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с
величинами, которые изображаются векторами 
на плоскости: при изучении течения жидкости, задач теории упругости.
После создания теории комплексных чисел возник вопрос о существовании
“гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую
систему вида 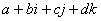 , где , где 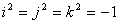
, построил в 1843 году ирландский математик У. Гамильтон, который назвал их
“кватернионами”.
Большой вклад в развитие теории функций комплексного переменного внесли
русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к
упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н.
Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.
Поняття комплексного числа.
“Подобно тому, как всю область действительных величин можно представить с
помощью бесконечной прямой, можно себе представить область всех величин,
действительных и мнимых, с помощью бесконечной плоскости, где каждая точка,
определенная своей абсциссой а и своей ординатой b, представляет в то же время
величину a+ib”.
Гаусс
Рассмотрим множество чисел, каждое из которых определяется упорядоченной парой
действительных чисел. Действительные числа будем обозначать буквами а, b, с,
..., а упорядоченные пары действительных чисел — буквами α, β,
γ, ... и соответственно записывать α=(a, b), β =(c, d) и т. д.
Такую упорядоченную пару действительных чисел (a,b) назовем комплексным
числом.
Определим действия над упорядоченными парами действительных чисел. Суммой
двух упорядоченных пар α= (а, b) и β = (с, d) назовем упорядоченную
пару γ = (a+c, b+d):
(a, b) + (c, d) = (a + c, b + d),
(1)
а произведением указанных пар — упорядоченную пару δ = (ас – bd, ad + bc):
(a, b)(c, d) = (ac – bd, ad + bc). (2)
Действия сложения и умножения упорядоченных пар действительных чисел
определены аксиоматически.
Для этих действий существуют обратные действия — вычитание и деление (кроме
деления на нуль). Разностью α — β двух упорядоченных пар
α = (a, b) и β = (с, d) назовем такую упорядоченную пару (х, y), для
которой (с, d) + (x, y) = (a, b). Принимая во внимание равенство (1), получаем
с + х = a, d + y = b, откуда x = а – c, y = b – d. Разностью α — β
упорядоченных пар α = (а, b) и β = (с, d) является упорядоченная
пара (а – c, b – d):
(a, b) – (c, d) = (a – c, b – d). (3)
Нулем служит пара 0 = (0, 0). Упорядоченной парой, противоположной для
упорядоченной пары α = (а, b) будет, пара - α = ( -а, -b), так как
α + (-α) = (а, b) + (-а, -b) = (0,0) = 0.
Частным от деления упорядоченной пары α = (а, b) на упорядоченную
пару β = (с, d), где β 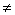
0 или с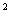 + d + d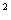 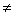
0 (т. е. хотя бы одно из чисел с, d отлично от нуля) должна быть упорядоченная
пара (x, y) такая, что (с, d) (x, y) = (а, b). Отсюда на основании равенства
(2) получаем cx – dy = a, cy – dx = b. Из этой системы уравнений находим x и y:
x = 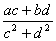 , y = , y = 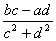 . .
Итак, если β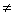 0, 0,
то частное α/β двух упорядоченных пар α = (а, b), β = (с,
d) существует и определяется формулой:
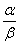 = = 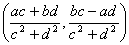 . (4) . (4)
Положив в этой формуле β = α (т. е. c = a, d = b), найдем, что
единицей при умножении упорядоченных пар служит упорядоченная пара (1, 0).
Полагая α = 1 = (1, 0), из формулы (4) получаем, что при β 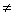
0 упорядоченной парой, обратной для β, будет упорядоченная пара
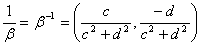 . .
Таким образом, построено множество чисел, действия над которыми определяются по
формулам (1) - (4). Это множество чисел называют множеством комплексных
чисел.
Докажем, что множество комплексных чисел в качестве своего подмножества
содержит все действительные числа. Рассмотрим упорядоченные пары вида (a,
0). Каждой паре (a, 0) поставим в соответствие действительное число а, в
результате получим взаимно однозначное соответствие между множеством
рассматриваемых упорядоченных пар и множеством всех действительных чисел.
Применяя к указанным упорядоченным парам формулы (1) и (2), находим;
(а, 0) + (b, 0) = (а + b, 0); (а, 0) (b, 0) = (ab, 0).
Эти равенства означают, что упорядоченные пары вида (а, 0) складываются и
умножаются так же, как действительные числа. Следовательно, множество
указанных упорядоченных пар действительных чисел, рассматриваемое как
подмножество множества комплексных чисел, по своим алгебраическим свойствам
не отличается от множества действительных чисел. Это позволяет положить
(а, 0) = а, (5)
т. е. не различать упорядоченную пару (a, 0) действительных чисел и
действительное число a. В частности, нуль (0, 0) и единица (1, 0) множества
комплексных чисел оказываются обычными действительными числами 0 и 1.
Покажем, что среди комплексных чисел содержится корень уравнения х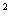
+ 1 = 0. Корнем уравнения х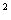
+ 1 = 0 является такое число, квадрат которого равен действительному числу —1.
Это число определяется упорядоченной парой (0, 1). В самом деле, применив
формулу (2), получим
(0, 1) (0, 1) = (-1, 0) = -1.
Обозначим эту упорядоченную пару через i, т. е. i = (0, 1), тогда
i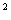 = - 1, i = = - 1, i = 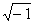 , (6) , (6)
число ί называют мнимой единицей.
Найдем произведение действительного числа b на упорядоченную пару (0, 1) =
ί — мнимую единицу:
bi = (b, 0)(0, 1) = (0, b), ib = (0, 1)(b,
0) = (0, b). (7)
Если (а, b) - произвольная упорядоченная пара, то из очевидного равенства (а,
b) = (a, 0) + (0, b) и формул (5), (7) получаем
(a, b) = a + bi. (8)
Следовательно, комплексное число α = (a, b) может быть записано в виде a +
bi = a + ib, где a и b — действительные числа, ί —
мнимая единица, определяемая соотношением (6). Выражение a + bi называют
алгебраической формой комплексного числа. Число a называют
действительной, число b — мнимой частью комплексного числа a + bi.
Обозначая комплексное число a + bi одной буквой α, пишут:
a = Reα, b = Imα,
где Re — начальные буквы латинского слова realis (действительный), Im -
начальные буквы латинского слова imaginarius (воображаемый). Кроме
указанных обозначений, употребляются также и такие: a = R(α), b =
I(α), где (a, b) = a + bi. Числа вида bi называют чисто
мнимыми числами или просто мнимыми.
Комплексное число a + bi считают равным нулю тогда и только тогда, когда
а = 0, b = 0:
 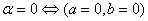 . (9) . (9)
Два комплексных числа a + bi и c + di считают равными
тогда и только тогда, когда равны между собой соответственно их действительные и
мнимые части, т. е. a = с, b = d:
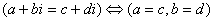 . (10) . (10)
Комплексное число a - bi называют сопряженным комплексному числу
a + bi. Обозначим число a - bi буквой 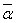
= a + bi. Числу 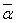
будет сопряжено число a – (-bi) = a + bi = α. Вследствие
этого числа α = a + bi и 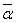
= a - bi называют комплексно сопряженными числами.
Действительные числа и только они сопряжены сами себе. В самом деле, если
α = a, где a - действительное число, то из формул (5) и (8) имеем: α
= a + 0i = a, 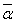
= a – 0i = a, т. е. α = 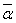
.
Например: комплексному числу 3 + 5i сопряжённым будет 3 – 5i ;
комплексному числу 4 - 7i сопряжённым будет 4 + 7i .
Действия над комплексными числами, заданными в алгебраической форме
Рассмотрим правила, по которым производятся арифметические действия над
комплексными числами.
Если даны два комплексных числа α = a + bi и β = c + di, то
Страницы: 1, 2, 3, 4, 5, 6
| 


