|
α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,
α – β = (a + bi) – (c + di) = (a – c) + (b – d)i
. (11)
Это следует из определения действий сложения и вычитания двух упорядоченных пар
действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и
вычитания комплексных чисел: чтобы сложить два комплексных числа, надо
отдельно сложить их действительные части и соответственно мнимые части; чтобы
из одного комплексного числа вычесть другое, необходимо вычесть
соответственно их действительные и мнимые части.
Число – α = – a – bi называют противоположным числу α
= a + bi . Сумма двух этих чисел равна нулю: - α + α = (- a -
bi) + (a + bi) = (-a + a) + (-b + b)i = 0.
Для получения правила умножения комплексных чисел воспользуемся формулой
(6), т. е. тем, что i2 = -1. Учитывая это соотношение,
находим (a + bi)( c + di) = ac + adi + bci + bdi
2 = ac + (ad + bc)i – bd, т.е.
(a + bi)( c + di) = (ac - bd) + (ad + bc)i . (12)
Эта формула соответствует формуле (2), которой определялось умножение
упорядоченных пар действительных чисел.
Отметим, что сумма и произведение двух комплексно сопряженных чисел являются
действительными числами. В самом деле, если α = a + bi, 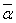
= a – bi, то α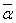
= (a + bi)( a - bi) = a2 – i2b2
= a2 + b2 , α + 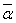
= ( a + bi) + (a - bi) = (a + a) + (b - b)i = 2a, т.е.
α + 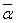 = 2a, = 2a,
α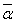 = a2 = a2
+ b2. (13)
При делении двух комплексных чисел в алгебраической форме следует
ожидать, что частное выражается также числом того же вида, т. е. α/β
= u + vi, где u, v 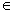
R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + b
i, β = c + di, причем β ≠ 0, т. е. c2 + d
2 ≠ 0. Последнее неравенство означает, что c и d одновременно в
нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу
(12) и второе из равенств (13), находим:
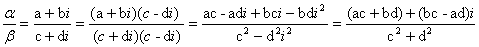
.
Следовательно, частное двух комплексных чисел определяется формулой:
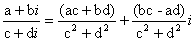 , (14) , (14)
соответствующей формуле (4).
С помощью полученной формулы для числа β = с + di можно найти
обратное ему число β-1 = 1/β. Полагая в формуле (14) а
= 1, b = 0, получаем
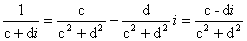 . .
Эта формула определяет число, обратное данному комплексному числу, отличному
от нуля; это число также является комплексным.
Например: (3 + 7i) + (4 + 2i) = 7 + 9i;
(6 + 5i) – (3 + 8i) = 3 – 3i;
(5 – 4i)(8 – 9i) = 4 – 77i;
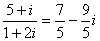 . .
Свойства действий
над комплексными числами
Для любых комплексных чисел α = a + bi, β = с + di,
γ = e + fi выполняются следующие свойства действий сложения и
умножения:
1) α + β = β + α – переместительное (коммутативное)
свойство сложения;
2) (α + β) + γ = α + (β + γ) – сочетательное
(ассоциативное) свойство сложения;
3) αβ = βα – переместительное (коммутативное) свойство
умножения;
4) (αβ)γ = α(βγ) – сочетательное
(ассоциативное) свойство умножения;
5) (α + β)γ = αγ + βγ – распределительное
(дистрибутивное) свойство умножения относительно сложения.
Докажем, например, первое и третье из этих свойств. По определению сложения
получаем
α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,
β + α = (c + di) + (a + bi) = (c + a) + (d + b)i =
(a + c) + (b + d)i = α + β,
так как с + a = a + с, d + b = b + d, т. е. для любых действительных чисел
выполняется переместительное (коммутативное) свойство сложения. Далее,
αβ = (a + bi)(c + di) = aс + adi + bci +
bdi2 = (ac - bd) + (ad + bc)i,
βα = (c + di) (a + bi) = сa + cbi + dai +
dbi2 = (ca - db) + (cb + da)i = (ac - bd) + (ad + bc)
i = αβ,
поскольку для любых действительных чисел ac = ca, bd = db, т. е. выполняется
переместительное (коммутативное) свойство умножения.
Остальные свойства доказываются аналогично, с учетом соответствующих свойств
операций над действительными числами.
Таким образом, операции над комплексными числами подчиняются тем же законам,
что и операции над действительными числами.
Возведение в степень комплексного числа.
Извлечение корня из комплексного числа
При возведении в степень комплексного числа пользуются формулой бинома Ньютона:
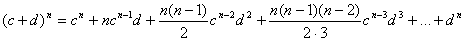
.
С помощью формулы бинома Ньютона получаем
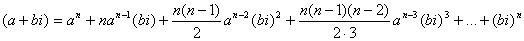
.
В правой части этого равенства заменяют степени мнимой единицы i их
значениями и приводят подобные члены. Рассмотрим, как выражаются эти степени.
Учитывая формулу i2 = - 1 , получаем i3 =
i2 ∙ i = -1 ∙ i = - i, i4
= i3 ∙ i = -i ∙ i = -i
2 = 1, i5 = i4 ∙ i = i, i6 =
i5 ∙ i = i2 = -1, i7 =
i6 ∙ i = -i, i8 = i7
∙i = - i2 = 1 и т. д. В общем виде полученный
результат можно записать так:
i4k = 1, i4k+1 = i, i4k+2 = -1, i4k+3 = - i (k = 0, 1, 2, .).
Например: (3 + 4i)2 = 32 + 2 ∙ 3
∙ 4i + (4i)2 = 9 + 24i + 16i2
= 9 + 24i – 16 = -7 + 24i;
(1 + i)3 = 1 + 3i + 3i2 + i3 = 1 + 3i – 3 – i = - 2 + 2i.
Переходим к извлечению квадратного корни из комплексного числа a + bi.
Квадратным корнем из комплексного числа называют такое комплексное число,
квадрат которого равен данному комплексному числу. Обозначим это комплексное
число через u + vi, т. е.
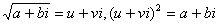 . .
Последнее равенство перепишем в следующем виде:
u2 + 2uvi + v2i2 = a + bi, u2 – v2 + 2uvi = a + bi.
Учитывая определение равенства комплексных чисел (см. (10)), получаем
u2 – v2 = a, 2uv = b. (15)
Возведем в квадрат обе части каждого из этих равенств, сложим их, преобразуем
полученную левую часть и извлечем квадратный корень:
(u2 – v2)2 + 4u2v2 = a2 + b2, (u2 + v2)2 = a2 + b2, u2 + v2 = 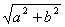 . .
Это уравнение и первое из уравнений (15) дают возможность определить u2 и v2 :
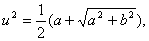 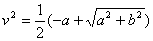 . (16) . (16)
Из первого уравнения находим два значения u, отличающиеся друг от друга
только знаком, второе уравнение дает два значения v. Все эти значения будут
действительными, поскольку при любых a и b
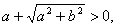 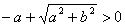 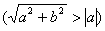 . .
Знаки u и v следует выбирать так, чтобы выполнялось второе из равенств (15). Это
дает две возможные комбинации значений u и v, т. е. два числа u1 + v
1i, u2 + v2i, отличающиеся знаком.
Следовательно, извлечение квадратного корня из комплексного числа всегда
возможно и дает два значения, отличающиеся друг от друга только знаком.
Например: пусть требуется извлечь квадратный корень из комплексного числа
3 — 4i, т. е. найти комплексное число u + vi такое, что (u + v
i)2 = 3 – 4i. В данном случае a = 3, b = -4, поэтому
уравнения (16) принимают вид
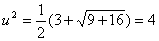 , , 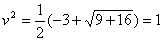 . .
Второе из равенств (15) запишется так: 2uv = - 4, uv =-2; это означает, что
соответствующие значения u и v имеют разные знаки. Так как u2 = 4,
v2 = 1, то с учетом равенства uv = -2 находим, что u1 =
2, v1 = -1, u2 = -2, v2 = 1, т.е. 2 – i
и -2 + i – значения квадратного корня из комплексного числа 3 – 4
i.
Геометрическое изображение комплексного числа
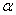 (a,b) (a,b)
|
|
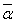 (a,b) (a,b)
|
|
Страницы: 1, 2, 3, 4, 5, 6
| 


